【人工智能】— 贝叶斯网络

频率学派 vs. 贝叶斯学派
贝叶斯学派
Probability（概率）:
独立性/条件独立性：
Probability Theory（概率论）:
Graphical models （概率图模型）
- 什么是图模型（Graphical Models）
- 图是什么
- 计算机科学中的图模型：
- 为什么图模型有用？
- 图模型：统一框架
- 图模型在机器学习中的作用：
- 图的方向性：
贝叶斯网络
- 举例说明：
- 举例说明：
Compactness（紧致性）
全局语义
局部语义
因果链
共同原因
共同效应
构建贝叶斯网络

频率学派 vs. 贝叶斯学派

频率学派:

概率是事件发生的长期预期频率。
P(A) = n/N，其中n是事件A在N次机会中发生的次数。
"某事发生的概率是0.1"意味着0.1是在无穷多样本的极限条件下能够被观察到的比例。
在许多情况下，不可能进行重复实验。
例如问题：第三次世界大战发生的概率是多少？

贝叶斯学派

概率是信念的度量。
它是一种基于不完全知识给出事件可能性的度量。
贝叶斯分析从先验信念开始，根据新的数据更新这种信念。
贝叶斯概率的主观性可能是一个限制，因为不同的人可能有不同的先验信念，并且可能根据相同的数据以不同的方式更新他们的信念。

Probability（概率）:

Probability（概率）是对不确定知识一种严密的形式化方法。
它提供了一种量化不同事件或结果的可能性的方式。
全联合概率分布指定了对随机变量的每种完全赋值，即每个原子事件的概率。
可以通过把对应于查询命题的原子事件的条目相加的方式来回答查询。
对于复杂的领域，联合分布可能会变得过于复杂，我们必须找到一种方法来减少它的大小。
独立性和条件独立性提供了分解联合分布和简化计算的工具。

独立性/条件独立性：

当且仅当 $P (A ∣ B) = P (A)$ ，或 $P (B ∣ A) = P (B)$ ，或 $P (A, B) = P (A) P (B)$ 时，A和B是独立的。
如果 $P (A ∣ B, C) = P (A ∣ C)$ ，则在给定C的条件下，A对于B是条件独立的。
在大多数情况下，使用条件独立性可以将全联合概率的表示从指数关系减少为线性关系。
条件独立性是我们关于不确定环境最基本和最强大的知识形式。
它可以简化复杂模型和更有效地进行推断。

Probability Theory（概率论）:

概率论可以用两个简单的方程式表达:
- 加法规则（Sum Rule）： $\sum_Y P(X,Y)$ ，通过边缘化或求和其他变量来获得变量的概率。
- 乘法规则（Product Rule）： $P (X, Y) = P (X ∣ Y) P (Y)$ ，联合概率可以用条件概率表达。
所有的概率推断和学习都可以归结为不断应用加法规则和乘法规则。

Graphical models （概率图模型）

什么是图模型（Graphical Models）

图模型是概率分布的图表表示。
它是概率论和图论的结合。
也被称为概率图模型（Probabilistic Graphical Models）。
它们增强了分析，而不是使用纯代数。

图是什么

由节点（也称为顶点）和链接（也称为边或弧）组成。
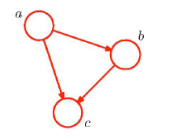
在概率图模型中，
- 每个节点表示一个随机变量（或一组随机变量）。
- 链接表示变量之间的概率关系。

计算机科学中的图模型：

处理不确定性和复杂性的自然工具，这些概念贯穿应用数学和工程。
图模型的基本思想是模块化，即通过组合较简单的部分来构建复杂的系统。
图模型为许多领域提供了一种有效的建模和推断方法，如人工智能、机器学习、计算机视觉和自然语言处理等。

为什么图模型有用？

概率理论提供了粘合剂，通过它，各部分得以结合，从而确保整个系统的一致性，并为模型与数据之间提供接口。
图论方面提供了：
- 直观的可视化界面，使人类能够对高度交互的变量集进行建模。
- 数据结构，自然地适合设计高效的通用算法。
图模型为许多领域提供了一种有效的建模和推断方法，如人工智能、机器学习、计算机视觉和自然语言处理等。

图模型：统一框架

将经典的多元概率系统视为共同的基础形式，如混合模型、因子分析、隐马尔可夫模型、卡尔曼滤波器等。
在系统工程、信息理论、模式识别和统计力学等领域中遇到。
观点的优点：
- 可以在不同领域之间转移和利用特定技术。
- 为设计新系统提供自然框架。
图模型为许多领域提供了一种有效的建模和推断方法，如人工智能、机器学习、计算机视觉和自然语言处理等。

图模型在机器学习中的作用：

形象化概率模型的结构，提供了一种简单的可视化方式。
通过检查图，可以深入了解模型的属性，如条件独立性属性。
需要进行推断和学习的复杂计算可以表示为图操作，从而简化了计算过程。

图的方向性：

有向图模型
- 箭头表示方向性。
- 贝叶斯网络
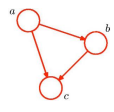
  - 表示随机变量之间的因果关系。
- 在人工智能和统计学中更为流行。
无向图模型
- 没有箭头的链接。
- 马尔科夫随机场
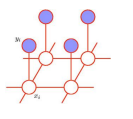
  - 更适合表示变量之间的软约束。
- 在视觉和物理学中更为流行。

贝叶斯网络

贝叶斯网络是一种简单的、图形化的数据结构，用于表示变量之间的依赖关系（条件独立性），为任何全联合概率分布提供一种简明的规范。

语法：
- 一个节点对应一个变量。
- 一个有向无环图（DAG）（链接≈“直接影响”）。
- 每个节点都有一个条件分布，给定其父节点的条件下的概率分布： $P(X_i | Parents(X_i))$ ，量化其父节点对该节点的影响。
在最简单的情况下，条件分布可以表示为一个条件概率表（CPT），给出每个父节点值组合下Xi的分布。

举例说明：

网络的拓扑结构编码了条件独立性的断言：

天气与其他变量无关。
在给定牙齿蛀牙的情况下，牙痛和牙感染（Catch）是条件独立的。

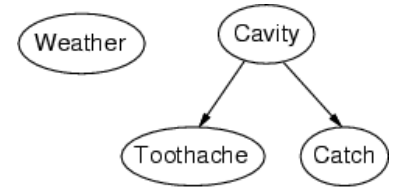
举例说明：

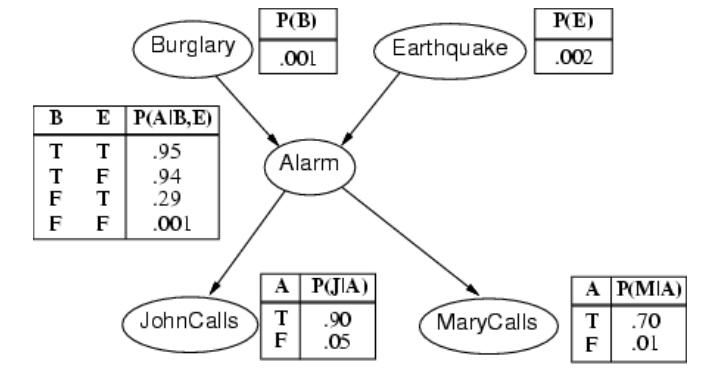
我正在工作，邻居约翰（John）打电话说我的闹钟响了，但邻居玛丽（Mary）没有打电话。有时它会因为小的地震而触发。这是不是有夜贼？

变量：入室行窃、地震、闹钟、約翰打电话、玛丽打电话。
网络拓扑反映了“因果”知识：

夜贼可以触发闹钟。
地震可以触发闹钟。
闹钟可以导致玛丽打电话。
闹钟可以导致约翰打电话。
- P(Burglary)
- P(Earthquake)
- P(Alarm | Burglary, Earthquake)
- P(JohnCalls | Alarm)
- P(MaryCalls | Alarm)
给定观测到的变量，可以进行推断，例如：
- 如果John报警，那么入室行窃的后验概率是多少？
- 如果没有人打电话，那么地震的后验概率是多少？
- 如果没有地震，也没有报警，那么入室行窃的后验概率是多少？

通过贝叶斯网络，可以直观地表达变量之间的依赖关系和条件独立性，从而进行推断和决策。
在这里插入图片描述

Compactness（紧致性）

一个具有k个布尔父节点的布尔变量的条件概率表中有 $2^k$ 个独立的可指定概率，对应于父节点值的组合。

每一行需要一个数字 $p$ ，表示 $X_i$ $=$ $t r u e$ 的概率（ $X_i$ $=$ $f a l se$ 的概率是 $1 - p$ ）。在这里插入图片描述

如果每个变量的父节点不超过k个，则完整的网络需要 $\cdot 2^k)$ 个数字。与完整的联合分布相比，其增长率是线性的，而不是 $O(2^n)$ 。

例如，对于入室行窃网络，有 $1 + 1 + 4 + 2 + 2 = 10$ 个数字（而全联合分布有 $2^{5}-1=31$ ）。

全局语义

在贝叶斯网络中，全联合概率分布可以表示为所有变量的条件概率分布的乘积，即：

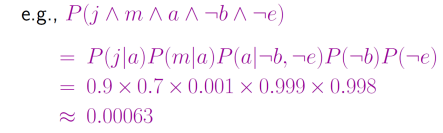
$P(X_{1},X_{2},...,X_{n}) = \prod_{i=1}^{n}P(X_{i}|Parents(X_{i}))$ 在这里插入图片描述

这个等式表明，联合概率分布可以完全由局部条件概率分布确定。这意味着，贝叶斯网络提供了一种紧凑、可解释、易于推断的方式来表示联合概率分布。

局部语义

局部语义指的是，给定父节点，一个节点与它的非后代节点是条件独立的。换句话说，每个节点只依赖于它的父节点和自身，与其他节点无关。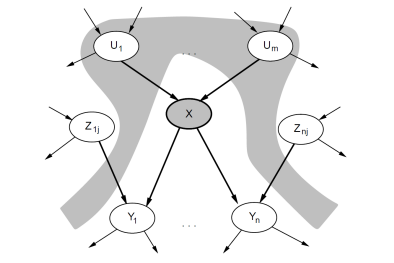在这里插入图片描述

定理：局部语义 $\Leftrightarrow$ 全局语义

即，全局语义中的联合概率分布可以由每个节点的条件概率分布表示，每个节点的条件独立性质可以保证全局条件独立性质。

因果链

基本结构
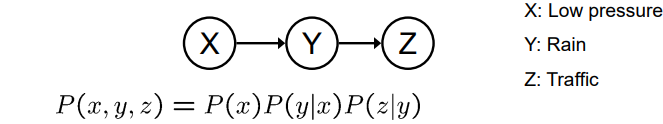
- 在给定Y的条件下，X是否与Z独立？
- 沿着链的证据“阻止”了影响。

因果链是一种基本的因果结构，其中一个变量直接影响另一个变量，从而构成一个链。例如，如果X导致Y，然后Y导致Z，那么这个结构就是一个因果链。

在因果链中，如果给定Y的条件下，X和Z是独立的，那么我们可以说Y是一个“阻碍变量”，它“阻止”了X对Z的影响。这种阻碍效应是因果推断的基础，因为它们提供了关于变量间因果关系的信息。

共同原因

另一个基本结构：同一原因的两个影响
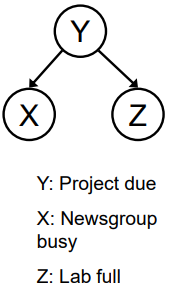
- X和Z是否独立？
- 在给定Y的条件下，X和Z是否独立？

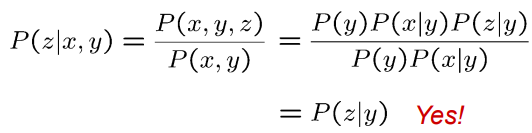
共同原因是另一个基本的因果结构，其中两个变量都受到同一原因的影响。例如，如果X和Z都是由Y导致的，那么这个结构就是一个共同原因。

在共同原因结构中，如果没有给定Y，那么X和Z可能会出现关联。但是，如果给定Y，则X和Z可能成为条件独立的，因为给定Y的情况下，它们的共同原因已经被控制。这种情况被称为“控制反应”，它提供了关于变量间因果关系的信息。

共同效应

• 最后一种结构：一个影响的两个原因（v-structures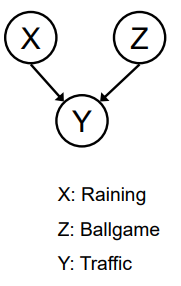）在这里插入图片描述

X和Z是否独立？
• 是：记住球赛和下雨导致交通堵塞，没有相关性吗？
在给定Y的条件下，X和Z是否独立？
• 不是：记住看到交通堵塞让雨和球赛处于竞争状态吗？
这与其他情况不同
• 观察效应可以使原因之间产生影响。

共同效应是一种因果结构，其中两个原因都可以导致同一效应。例如，如果X和Z都可以导致Y，那么这个结构就是一个共同效应。

在共同效应结构中，如果X和Z都是独立的，那么它们可能不会对Y产生影响，因为它们没有直接的关系。但是，如果给定了Y，则X和Z可能成为条件独立的，因为在给定Y的情况下，它们之间的影响路径被阻断了。这种情况被称为“掩蔽”，它提供了关于变量间因果关系的信息。

需要注意的是，观察到效应可能会导致原因之间产生影响，这与其他情况不同。例如，如果我们观察到交通堵塞，那么球赛和下雨可能会成为竞争因素，从而影响彼此的发生概率。这种情况是与其他情况相反的，因为观察到效应可以启用原因之间的影响。

构建贝叶斯网络

需要一种方法使得局部的条件独立关系能够保证全局语义得以成立。

选择变量 $X_1$ ， $X_2$ ，…， $X_n$ 的顺序。
对于 $i = 1$ 到 $n$ ，将 $X_i$ 添加到网络中，并从 $X_1$ ， $X_2$ ，…， $X_{i-1}$ 中选择父节点，使得条件概率符合以下条件：
$P(X_i|Parents(X_i)) = P(X_i|X_1,...,X_{i-1})$