目录

前言

文献阅读：基于BO-EMD-LSTM模型预测教室长期二氧化碳浓度

背景

思路

BO-EMD-LSTM 混合模型

EMD 算法

与其他模型的比较 

结论

论文代码

总结

---

前言

This week, I studied an article that uses LSTM to predict gas concentration.This study was designed to explore the long-term prediction of indoor CO2 concentrations to provide an early warning mechanism for indoor air quality. Based on the divide-and-conquer strategy, we proposed a hybrid BO–EMD–LSTM method by integrating BO algorithm, EMD algorithm and LSTM model, and conducted comparative experiments with benchmark models. The strategy by combing the signal decomposition algorithm and deep learning algorithm in this paper can significantly improve prediction performance. The results indicated that the accuracy of BO–EMD–LSTM model was higher than that of the benchmark models, which was improved by more than 55%.In addition to this, continue to learn the relevant code of kriging interpolation and LSTM combination.

本周学习了一篇基于LSTM来预测气体浓度的文章。本研究旨在探讨室内集中CO2的长期预测，为室内空气质量提供预警机制。基于分而治之策略，结合BO算法、EMD算法和LSTM模型，提出了一种混合BO-EMD-LSTM方法，并与基准模型进行了对比实验。该文将信号分解算法和深度学习算法相结合的策略可以显著提高预测性能。结果表明，BO-EMD-LSTM模型的准确率高于基准模型，提高了55%以上。除此之外，继续学习克里金插值和LSTM结合的相关代码。

文献阅读：基于BO-EMD-LSTM模型预测教室长期二氧化碳浓度

--Guangfei Yang, Erbiao Yuan, Wenjun Wu,
Predicting the long-term CO2 concentration in classrooms based on the BO–EMD–LSTM model,
Building and Environment,
Volume 224,
2022,
109568,
ISSN 0360-1323,
https://doi.org/10.1016/j.buildenv.2022.109568.

背景

人们每天大约三分之二的时间在室内度过，这使得室内环境质量成为研究人员的主要关注点。先前的研究表明，室内环境的污染程度至少是室外环境的两倍。长期暴露于高浓度二氧化碳（CO2）会对人类健康产生不利影响，降低学生的每日出勤率和考试成绩，并降低工人的生产力;然而，许多实验发现，教室的二氧化碳空气质量水平不符合室内空气质量标准。因此，控制课堂上的二氧化碳水平的有效措施是必不可少的。控制此类二氧化碳水平的常用方法是改善通风;但是，决定何时进行以及持续多长时间具有挑战性。基于长期精准预测室内CO2浓度的预警机制可以提供重要的参考。

思路

首先，采用经验模态分解（EMD）算法分解原始CO2 浓度序列分为几个固有模式函数 （IMF） 和一个残差函数。

其次，对每个子序列执行贝叶斯优化（BO），即超参数优化。

随后，利用优化后的超参数为每个子序列构建LSTM模型，该模型可以提前30分钟进行长期预测。

最后，对各子序列的所有预测结果进行综合，得出最终的预测结果。

BO-EMD-LSTM 混合模型

为了准确预测时间序列，我们提出了一种称为BO-EMD-LSTM的有效方法。如图 5 所示，CO2浓度的时间序列首先分解为几个子序列。该方法基于BO对LSTM模型的超参数进行滤波，使用得到的最优超参数。最后，对子序列的预测结果进行加法，得到最终结果。通过充分利用BO、EMD和LSTM网络，BO-EMD-LSTM模型可以预测长期集中于教室的CO2浓度。我们的模型创新性地将EMD算法引入深度学习模型，将复杂且频繁变化的时间序列分解为相对稳定的序列。深度学习模型更容易探索稳定序列中的变化规律，以提高长期预测的准确性。

​

EMD 算法

原始 CO2浓度序列可以视为动态信号。因此，可以应用信号处理的时频分析方法;然而，在傅里叶和小波变换中选择合适的基是一项艰巨的任务。数据驱动的EMD处理已被证明是一种有效的方法。EMD的优点是可以克服基本功能的不适应性，使信号分解更简单、更高效。具体来说，原始时间序列的数据被分解为残差和有限数量的IMF。IMF反映了信号的局部特征，必须满足两个条件：

（1）在整个数据段中，极值点和零点交叉点的数量必须相等，或者差值最多不能超过一个;

（2）在任何时候，由局部最大点形成的上包络线和由局部最小点形成的下包络线的平均值为零。

  EMD 算法的步骤如图所示。

​

与其他模型的比较 

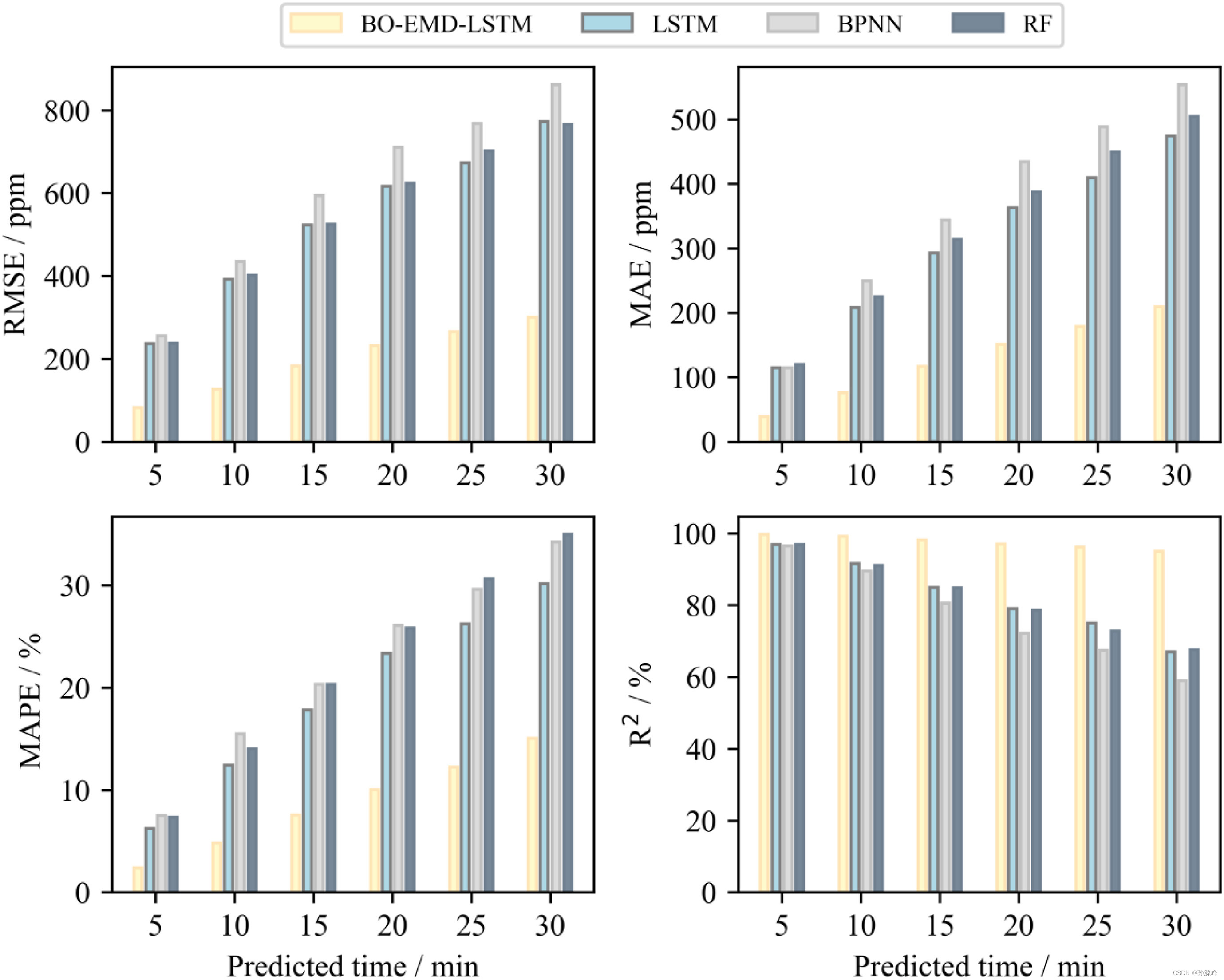
为了进一步验证BO-EMD-LSTM模型的预测性能，我们将其与LSTM，BPNN和RF模型进行了比较。 图 10 证明了 RMSE、MAE、MAPE 和 R2，LSTM的预测精度高于RF和BPNN，BO-EMD-LSTM模型优于LSTM模型，表明其在预测CO2集中于教室方面的稳定性和效率。

教室二氧化碳浓度预测中，LSTM、BPNN和RF模型具有相似的性能;然而，BO-EMD-LSTM模型的精度提高是显而易见的。当预测时间为5–30 min时，BO-EMD-LSTM模型的准确率提高了55%以上，最大提高幅度达到71.024%。具体而言，当预测时间为5 min时，基准模型的最小MAE为114.686 ppm，BO-EMD-LSTM的MAE为39.062 ppm;因此，准确度提高了65.940%。当预测时间增加到30 min时，基准模型的最小MAE为473.896 ppm，BO-EMD-LSTM的MAE为209.110 ppm;因此，准确度提高了55.874%。BO-EMD-LSTM模型对RMSE和MAPE具有相似的结果。此外，R2BO-EMD-LSTM模型的值非常稳定，在不同预测时间均超过95%。然而，R2其他3个模型的值随着预测时间的增加而迅速下降。R2的长期预测误差减少和稳定性表明BO-EMD-LSTM模型不仅具有良好的预测性能，而且具有较好的鲁棒性。

​

结论

本研究旨在探讨室内集中CO2的长期预测，为室内空气质量提供预警机制。基于分而治之策略，结合BO算法、EMD算法和LSTM模型，提出了一种混合BO-EMD-LSTM方法，并与基准模型进行了对比实验。该文将信号分解算法和深度学习算法相结合的策略可以显著提高预测性能。结果表明，BO-EMD-LSTM模型的准确率高于基准模型，提高了55%以上。此外，BO-EMD-LSTM模型在预测室内CO2浓度时更稳定。及其R2保持在95%以上。结果还表明，子序列的数量对预测有影响，通过将子序列与我们的方法合并可以节省更多的计算时间。本文提出的方法可能是预测室内CO2浓度的有效方法并帮助决策者实施控制措施以改善室内空气质量。

论文代码

普通克里金插值中半方差的计算 

import numpy as np

# 定义距离函数
def dist(x1, x2):
    return np.sqrt(np.sum((x1 - x2) ** 2))

# 定义克里金半方差函数
def kriging_vario(point, data, model, h_range):
    # 计算距离矩阵
    dist_matrix = np.zeros((len(data), len(data)))
    for i in range(len(data)):
        for j in range(i+1, len(data)):
            dist_matrix[i,j] = dist(data[i,:-1], data[j,:-1])
            dist_matrix[j,i] = dist_matrix[i,j]

    # 计算半方差
    vario = np.zeros(h_range)
    for h in range(h_range):
        idx = np.where(dist_matrix < (h+1))[0]
        if len(idx) > 0:
            vario[h] = np.sum((data[idx,-1] - np.mean(data[idx,-1]))**2) / len(idx)

    return vario

# 测试数据
data = np.array([[0, 0, 1],
                 [2, 0, 2],
                 [0, 2, 3],
                 [2, 2, 4]])

# 待预测点
point = np.array([1, 1])

# 模型参数
model = {'sill': 1.0, 'range': 1.0, 'nugget': 0.0}

# 计算半方差
vario = kriging_vario(point, data, model, 5)

print(vario)

训练lstm

import numpy as np

class LSTM:
    def __init__(self, input_dim, hidden_dim):
        self.input_dim = input_dim
        self.hidden_dim = hidden_dim
        
        # 初始化LSTM模型的参数
        # 输入门参数
        self.W_ii = np.random.randn(input_dim, hidden_dim)
        self.W_hi = np.random.randn(hidden_dim, hidden_dim)
        self.b_i = np.zeros((1, hidden_dim))
        
        # 遗忘门参数
        self.W_if = np.random.randn(input_dim, hidden_dim)
        self.W_hf = np.random.randn(hidden_dim, hidden_dim)
        self.b_f = np.zeros((1, hidden_dim))
        
        # 输出门参数
        self.W_io = np.random.randn(input_dim, hidden_dim)
        self.W_ho = np.random.randn(hidden_dim, hidden_dim)
        self.b_o = np.zeros((1, hidden_dim))
        
        # 记忆细胞参数
        self.W_ic = np.random.randn(input_dim, hidden_dim)
        self.W_hc = np.random.randn(hidden_dim, hidden_dim)
        self.b_c = np.zeros((1, hidden_dim))
        
        # 初始化状态和记忆向量
        self.h = None
        self.c = None
    
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))
    
    def tanh(self, x):
        return np.tanh(x)
    
    def forward(self, x):
        # x.shape = (batch_size, sequence_length, input_dim)
        batch_size, sequence_length, _ = x.shape
        
        h = np.zeros((batch_size, sequence_length, self.hidden_dim)) # 保存每个时间步的隐藏状态
        c = np.zeros((batch_size, sequence_length, self.hidden_dim)) # 保存每个时间步的记忆向量
        
        for t in range(sequence_length):
            x_t = x[:, t, :] # 选择当前时间步的输入
            
            # 计算输入门i
            i_t = self.sigmoid(np.dot(x_t, self.W_ii) + np.dot(h[:, t-1, :], self.W_hi) + self.b_i)
            
            # 计算遗忘门f
            f_t = self.sigmoid(np.dot(x_t, self.W_if) + np.dot(h[:, t-1, :], self.W_hf) + self.b_f)
            
            # 计算输出门o
            o_t = self.sigmoid(np.dot(x_t, self.W_io) + np.dot(h[:, t-1, :], self.W_ho) + self.b_o)
            
            # 计算记忆细胞c
            c_t = f_t * c[:, t-1, :] + i_t * self.tanh(np.dot(x_t, self.W_ic) + np.dot(h[:, t-1, :], self.W_hc) + self.b_c)
            
            # 更新隐藏状态h
            h_t = o_t * self.tanh(c_t)
            
            # 保存当前时间步的隐藏状态和记忆向量
            h[:, t, :] = h_t
            c[:, t, :] = c_t
        
        # 保存最后一个时间步的隐藏状态和记忆向量
        self.h, self.c = h[:, -1, :], c[:, -1, :]
        
        return self.h

总结

目前的主要任务是深度的学习代码，希望尽早能将论文目标具体化。