vx = 100*cos(1/3*pi);
vy = 100*sin(1/3*pi);
t = 0:0.005:18;
x = vx*t;
y = vy*-9.8*t.^2/2;
comet(x,y)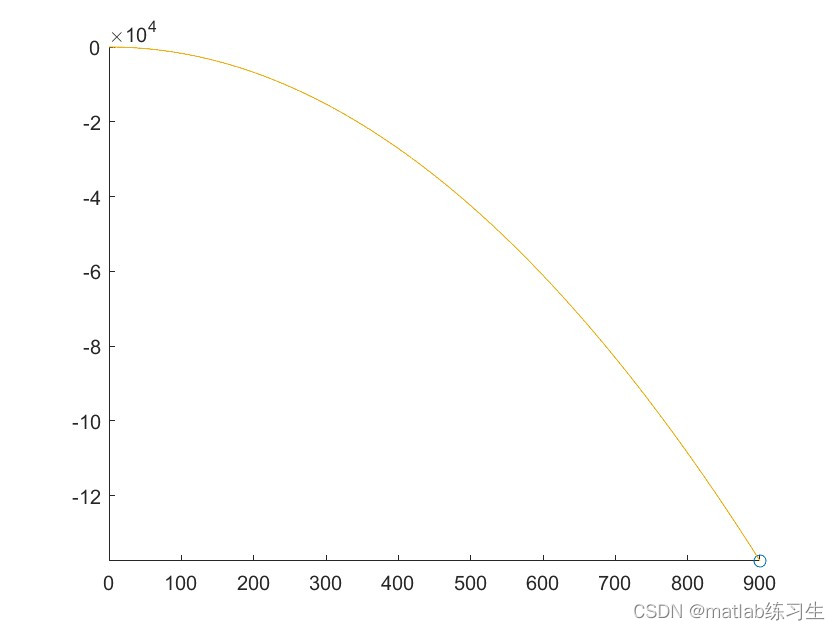

 这里只是截取了最后的画面，正常运行时，可以看到从最高点向下落的动作。

想要了解这段代码，我们要知道comet函数的意义

这个函数可以沿着向量移动的彗星，彗星是由标记（头部）和一条线（尾部）构成的动画，用于跟踪线条随数据点而不断变长的情况。尾巴是跟踪整个函数的实线。

也就是说，沿着向量延伸的方向绘制动画

上述代码中用的是抛物线的运动方程，设置了xy方向的初始速度和加速度（-9.8）

接下来，我们在三维空间绘制动画，比如绘制洛伦兹吸引子的三维动态图：

f1 = @(t,x)[-8/3*x(1)+x(2)*x(3);
    -10*(x(2)-x(3));
    -x(1)*x(2)+28*x(2)-x(3)];
%洛伦兹微分方程组
t_final = 100;
x0 = [0;0;1e-10];
[t,x] = ode45(f1,[0,t_final],x0);
figure
axis([10 42 -20 20 -20 25]);
comet3(x(:,1),x(:,2),x(:,3))

需要注意的是，comet3(x,y,z)显示 z 中指定的数据对与 z 的索引相匹配的 x 和 y 值的彗星图。

ode45是求解非刚性微分方程的函数，可以求微分方程组 y'=f(t,y) 从 t0 到 tf 的积分，初始条件为 y0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。

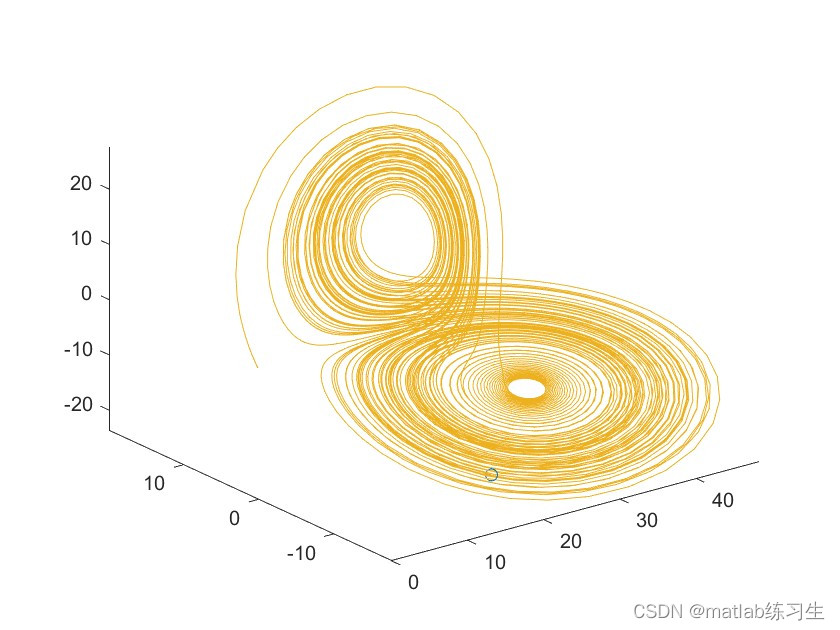
最后简单介绍一下洛伦兹吸引子：

洛伦兹吸引子由气象学家Edward Lorenz在1963年给出，来源于模拟大气对流，该模型除了在天气预报中有显著的应用之外，还可以用于研究空气污染和全球侯变化。

具体可以参考：
(10条消息) 走近分形与混沌(part5)--洛伦茨与吸引子_洛伦兹混沌吸引子_GoatGui的博客-CSDN博客https://blog.csdn.net/m0_37422217/article/details/105607085

参考《高等光学仿真——光波导、激光》