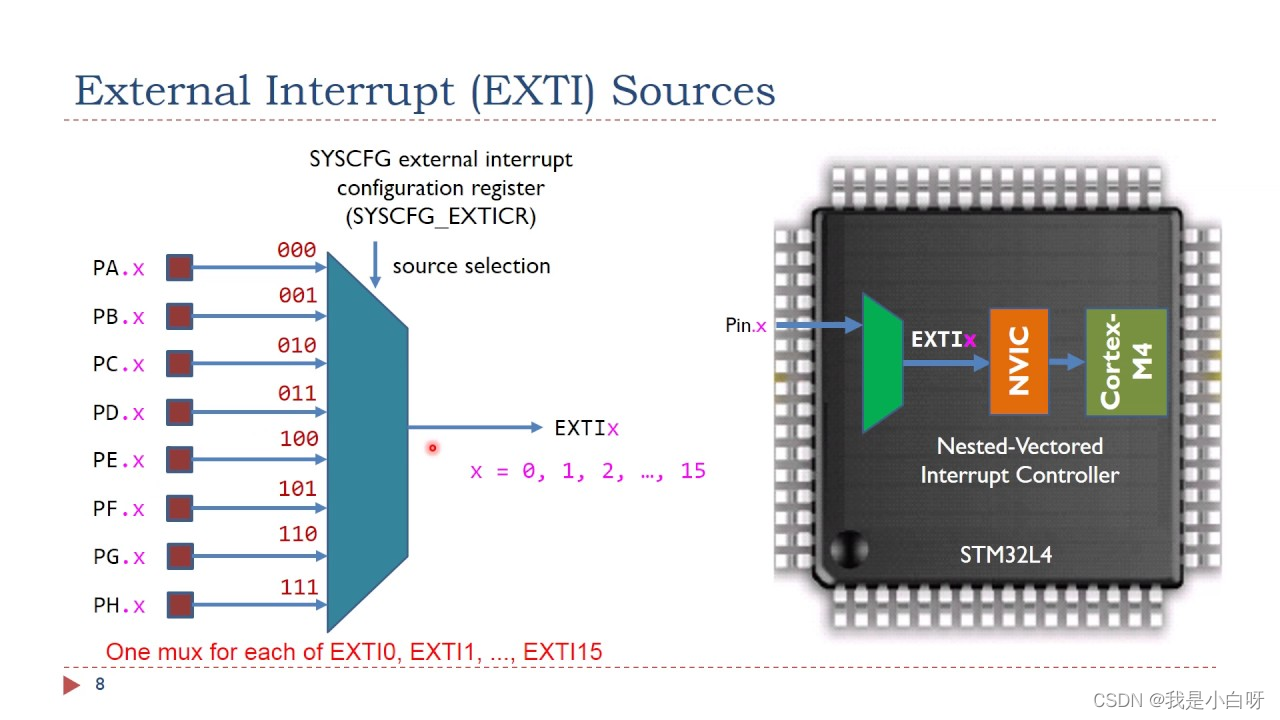
资本资产定价模型自从首次被提出以来在金融经济学中一直处于中心地位。 在一系列简化假定条件下,资本资产定价模型表明,任何证券的收益率与该证券 的系统性风险(或者贝塔值)呈线性关系。因此,依据资本资产定价模型横截面 收益率与风险的关系可以表示为:
E( Ri )= a0 + 1 a β i
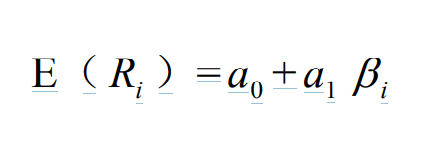
其中 E( Ri )表示单一股票的期望收益率, β i 代表该股票的贝塔值。如果 模型正确,而且证券市场有效,股票收益率平均来说应当满足这一线性关系。与 正线性相关关系的背离即表明,资本资产定价模型与有效市场假说的联合假定不 成立。 早期检验5 发现平均收益率与估计贝塔值存在显著的相关关系。早期检验存 在的问题是,大多数静态 CAPM 模型的实证检验假设贝塔值不随时间而改变, 而且使用所有股票的加权收益率作为市场收益率的代表变量。接下来的研究并不 是这样,Roll, R.(1977)批判了对于资本资产定价模型已有的检验,因为任何建立 在不同于真正的市场组合的“市场组合”基础上的检验都不是对于资本资产定价 模型的真正检验,Stambaugh, R.(1982)建立了包括债券、房地产以及耐用消费品 的更广泛的市场指数,运用这一指数对于模型进行检验,结果发现收益率对于这 一定义下的市场并不敏感。因此静态资本资产定价模型不成立的原因并不在于市 场收益率代表变量过于狭窄。 在接下来的研究当中,对于静态资本资产定价模型的改善朝着两个方向发 展。上世纪七十年代 Basu, S.(1977)和 Banz, R.(1981)分别发现市盈率(P/E)与普 通股股票市值(公司大小)都比贝塔值提供更多的解释效应。Fama, E.与 K. French(1992),DeBondt, W.与 R. Thaler(1985)将范围扩大到了包括市净率、每股 价格以及前期收益率表现。总体来看,这些研究提供了充分的证据表明股票横截 面收益率的可预测性,并大大降低了早期研究中贝塔值所具有的解释力量。在 CAPM 模型受到如此重大的挑战的情况之下,理论界迫切需要一个新的理论或者 解释来替代或者改善这一模型。例如,Fama 与 French(FF)(1993,1995,1996)提出 一种三因素模型,除了市场收益率以外,市净率以及市值大小被考虑进来。Fama 与 French(1997)使用这一模型来计算股票的资本成本。 有一部分学者朝另外一个方向发展,即改善 CAPM 的检验方法。例如 R. Jagannathan 与 Zhenyu Wang(1996)研究了条件 CAPM 模型解释大规模股票组 合平均收益率截面模式的能力,并且在考虑人力资本因素的情况下,条件 CAPM 能够很好的解释股票收益率。本文检验条件资本资产定价模型时就参照了这篇论 文所采用的模型。 中国学者也对于股票市场风险与收益关系做出了一些定量分析。陈小悦、姚
阿尔法策略是如何构建的?
阿尔法策略所涉及的市场领域非常广泛,在股市、债市、商品市场等各类市场都有应用。而目前国内市场上最常见的还是股市阿尔法对冲策略,其通常利用选股、择时等方面优势,寻找具有稳定超额收益的现货组合,通过股指期货等衍生工具来分离贝塔,进而获得与市场相关度较低的阿尔法收益。尤其是在熊市或者盘整期,可以采用“现货多头+期货空头”的方法,一方面建立能够获取超额收益的投资组合的多头头寸,另一方面建立股指期货的空头头寸以对冲现货组合的系统风险,从而获取正的绝对收益。此外,还有机构根据获取阿尔法的途径,采取统计套利、事件驱动、高频交易等策略来获取阿尔法收益。而在上述各种策略构建过程中,基于大类资产配置、行业配置、择时与选股体系的量化策略均得到了广泛应用。