1、背景

t检验是科研中非常常用的一种方法和手段，但是理解到位的人并不多，虽然这也不影响其使用。本文主要目的在于将与t检验有关的前前后后都讲明白。

2、补充知识

理解t检验，我们需要补充一些统计学有关的先验知识。

2.1 正态分布

概率密度函数为

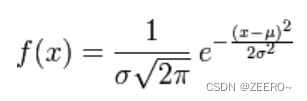
正态分布为自然界最常见的分布，注意，这个最后面没有之一。
图像如图所示

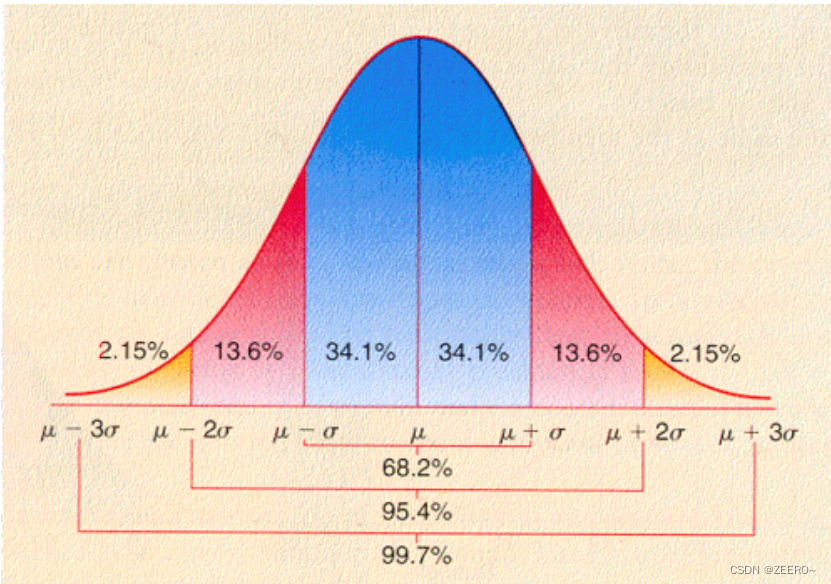
根据图像我们知道，我们来看下正态分布的几个性质：

1. 正态分布的概率密度函数为偶函数；
2. 概率密度函数关于x=$\mu$对称；
   3）标准差$\sigma$越大，分母越小，密度函数曲线越矮。
   这里，$1\sigma$区间对应的概率为68.4%，$2\sigma$对应的区间为95.4%，$3\sigma$对应的区间为99.7%。这3个较为常用。
   在统计学检验中的P值，我们通常会假定(P<0.05)，这里的0.05也是来自于这里。确切的说，当从均值$\mu$往左或往右各1.96倍标准差的时候，对应的左侧和右侧面积之和就是5%。因为这种概率不是很高，所以认为其是小概率事件。
   我们日常生活中常听到的六西格玛也是来自于这里。

2.2 自由度

自由度的定义是指计算样本统计量时能够自由取值的个数，一般用df来表示。举个例子，例如x+y+z=100，一旦y和z的值确定下来，那么x的值也就固定了，因此能够自由取值的个数只有2个，而不是3个，也就是说，自由度是2。
在不同的统计方法中，自由度都不一样，但基本原则是每估计1个参数，就需要消耗一个自由度。
几个典型场景：
1）在单样本t检验中，自由度是n-1。因为只需要估计1个参数，就需要消耗1个自由度，所以自由度是n-1。

2.3 t分布

2.3 卡方分布

定义：若n个相互独立的随机变量x1,x2,...xn均服从标准正态分布（$\mu=0,\sigma=1$），则这n个服从标准正态分布的随机变量的平方和构成的新的变量服从卡方分布【来源：百度百科】。

3、t检验

3.1 t检验统一的公式

$$t=\frac{样本统计量-总体参数}{样本统计量的标准差(标准误)}$$
上面为t检验的统一公式。
如果是2组之间进行比较（注意，t检验不仅是2组之间的比较，不要误以为t检验仅能用于2组间的比较），一般我们假定总体参数为2组差值=0,因此公式变换为
$$t=\frac{({\bar{x}}_1-{\bar{x}}_2)-0}{S_{{\bar{x}}_1-{\bar{x}}_2}}$$
解释一下，分子中的${\bar{x}}_1-{\bar{x}}_2$为样本统计量（两组均值之差），0是无效假设的总体参数，因此分子反映了样本统计量与总体参数的偏离程度，分母中的标准误则是样本统计量的标准差。
因此，t检验实际上是反映了相对样本统计量的标准差而言，样本统计量偏离总体参数的大小。