【MATLAB第31期】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理回归问题MATLAB代码实现(持续更新)

news2025/1/25 9:17:20

【MATLAB第31期】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理回归问题MATLAB代码实现(持续更新)

本文敏感性分析主要分析回归问题，下期分析分类问题（fisher、rf、arf、nca等）。

一、降维方法（回归）

常见的降维方法：
常见的敏感性分析法：

*（一）.全局敏感性分析（sobol、蒙特卡洛方法）

（二）.非全局敏感性分析
1.变量归类（主成分分析PCA、核主成分分析KPCA）
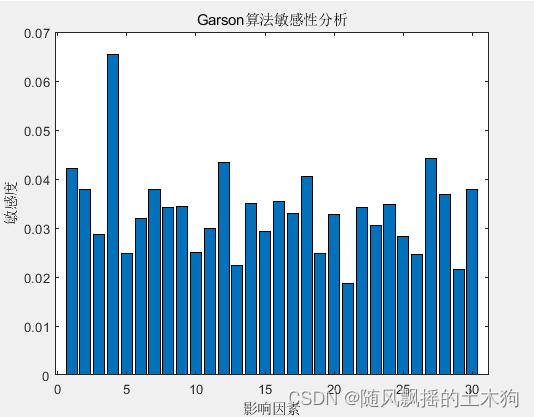
2.变量筛选（临近成分分析NCA、RF随机森林、ARF自适应随机森林、皮尔逊系数PCC、Relief-F、Term Variance、garson、极差分析法）
特征选择和降维
1、相同点和不同点
特征选择和降维有着些许的相似点，这两者达到的效果是一样的，就是试图去减少特征数据集中的属性(或者称为特征)的数目；但是两者所采用的方式方法却不同：降维的方法主要是通过属性间的关系，如组合不同的属性得新的属性，这样就改变了原来的特征空间；而特征选择的方法是从原始特征数据集中选择出子集，是一种包含的关系，没有更改原始的特征空间。
2、降维的主要方法
Principal Component Analysis(主成分分析)，详细见“简单易学的机器学习算法——主成分分析(PCA)”
Singular Value Decomposition(奇异值分解)，详细见“简单易学的机器学习算法——SVD奇异值分解”
Sammon’s Mapping(Sammon映射)
特征提取和特征选择都是从原始特征中找出最有效（同类样本的不变性、不同样本的鉴别性、对噪声的鲁棒性）的特征。
特征提取：将原始特征转换为一组具有明显物理意义（Gabor、几何特征[角点、不变量]、纹理[LBP HOG]）或者统计意义或核的特征
特征选择：从特征集合中挑选一组最具统计意义的特征，达到降维
两者作用：
1 减少数据存储和输入数据带宽
2 减少冗余
3 低纬上分类性往往会提高
4 能发现更有意义的潜在的变量，帮助对数据产生更深入的了解

二、案例数据

案例数据data 1000×31 ，前30列为变量，第31列为因变量
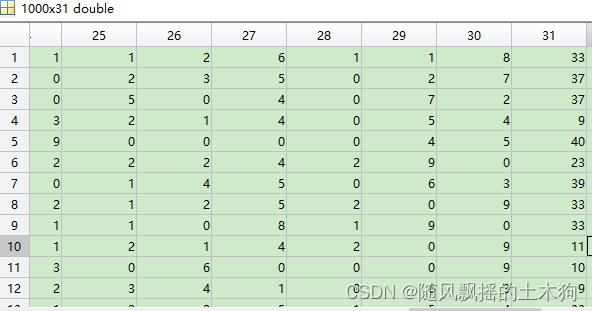
在这里插入图片描述

（1）主成分分析PCA

%% 1.降维方法
%
clc
clear all

load data
x=data(:,1:end-1);

%% (1)主成分分析PCA
addpath('D:\特征排序\PCA')
ContributeRate=0.9;  %贡献率90%
[xpca,result_report]=mypca(x,ContributeRate) ;

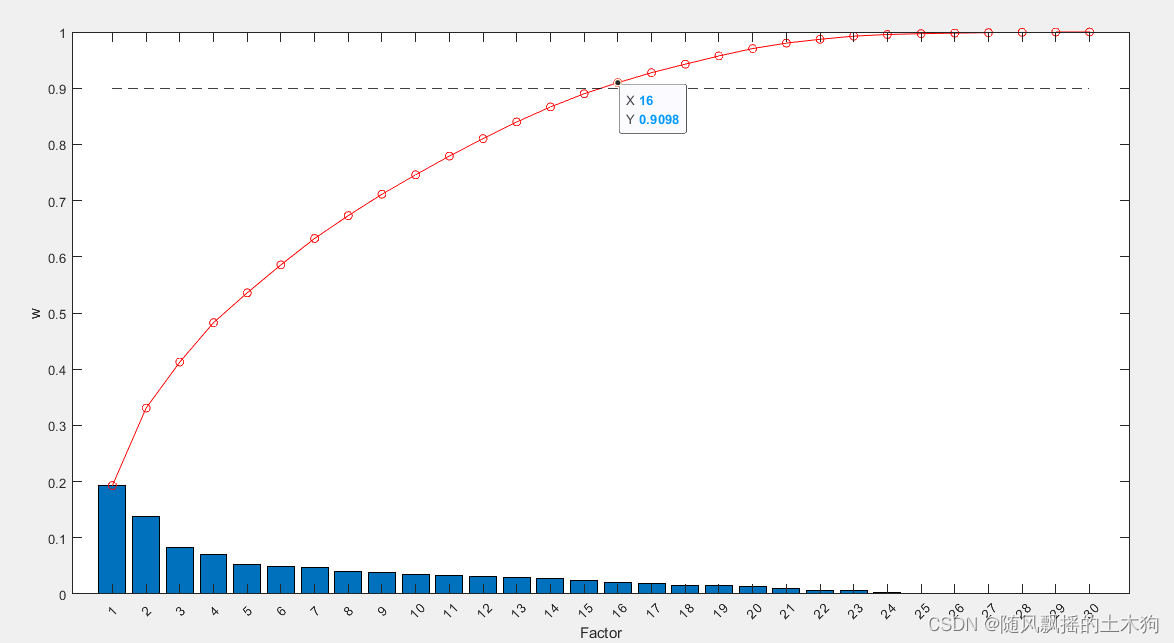
在这里插入图片描述
三十个变量通过降维成16个变量组合。

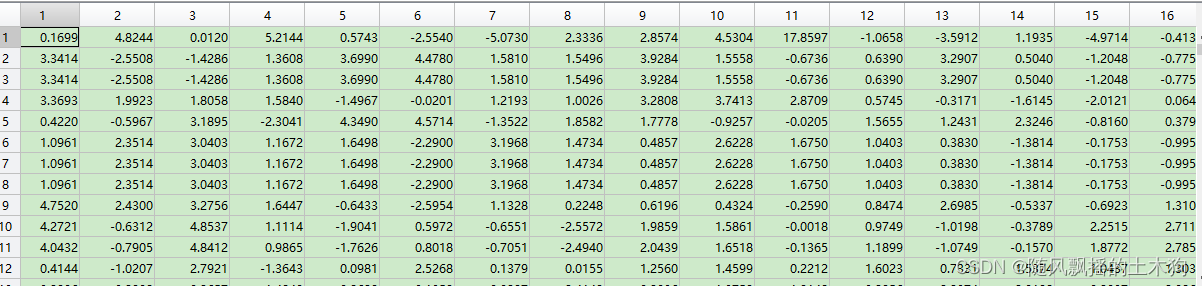
（2）核主成分分析KPCA

核函数可选择四种，分别为：
1-高斯核函数
2-二阶多项式核
3-线性核
4-sigmoid核（tanh）

%% (2)核主成分分析KPCA  
addpath('D:\特征排序\KPCA')
sigma=0.3;
ContributeRate=0.9;
KindKernel=2;% 1-高斯核函数，2-二阶多项式核，3-线性核，4-sigmoid核（tanh）
[xkpca] =kpca(x,sigma, KindKernel,ContributeRate);

当采用高斯核函数时，出现复数，结果报错。
故选择二阶多项式核进行运算得：
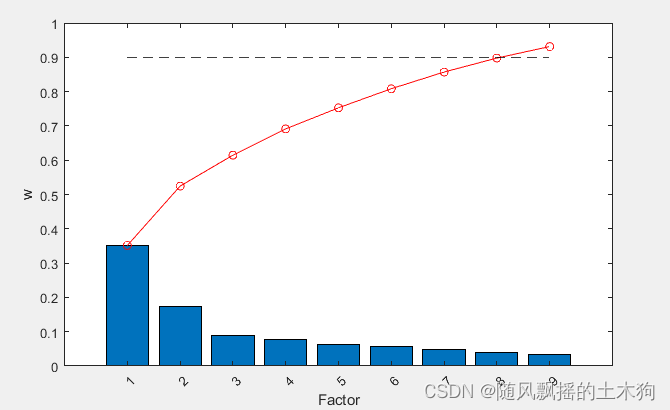
在这里插入图片描述
3-线性核运行结果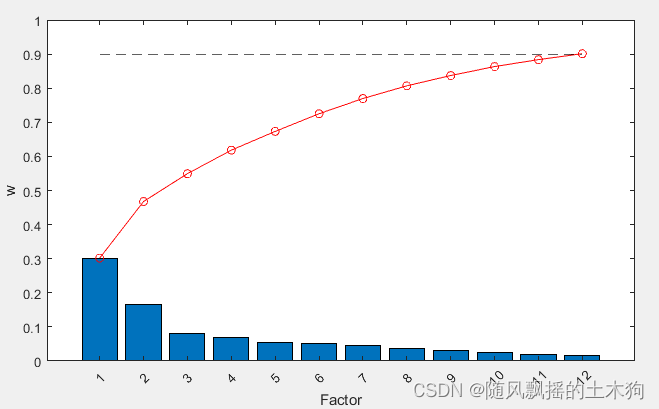

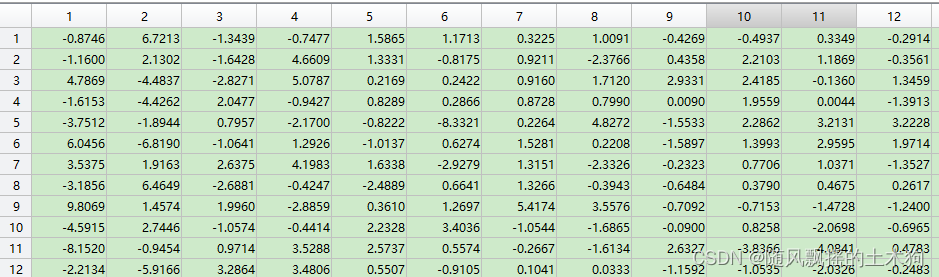
4-sigmoid核（tanh），出现复数，结果报错。

（3）临近成分分析NCA

%% (3)近邻成分分析NCA
addpath('D:\特征排序\NCA')
ContributeRate=0.9;
xtrain =data(:,1:end-1);
ytrain =data(:,end);
[xx,mdl]=myfsrnca(xtrain,ytrain,0.9);
xnca=data(:,xx);

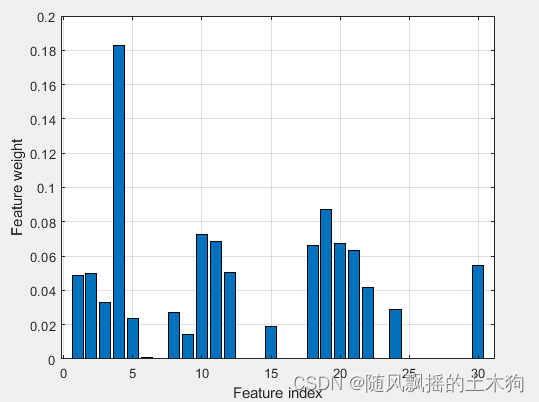
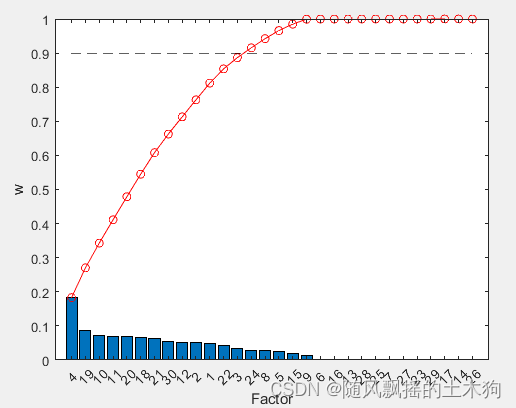
在这里插入图片描述

（4）随机森林RF

%% (4)随机森林RF
addpath('D:\特征排序\RF')
ContributeRate=0.9;
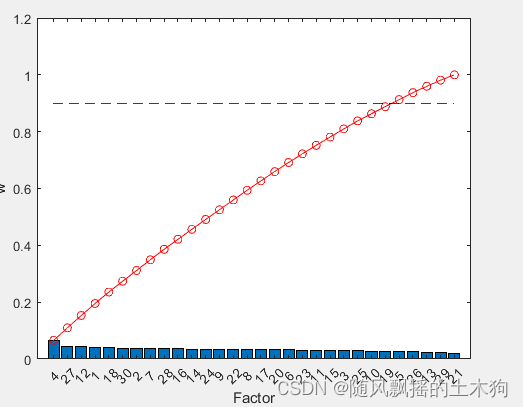
[XT,RFModel,w]= myrf(data,ContributeRate);
xrf=data(:,XT);

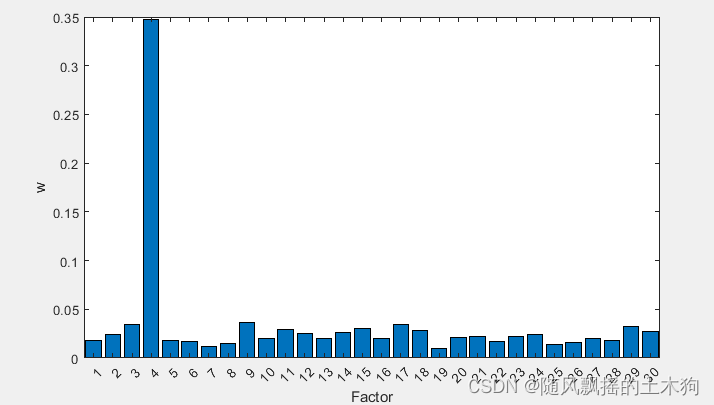
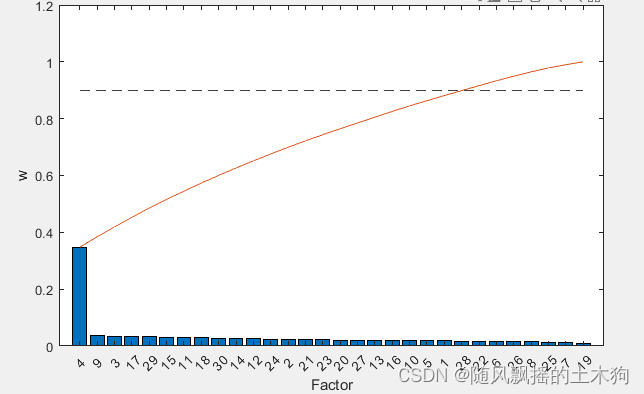
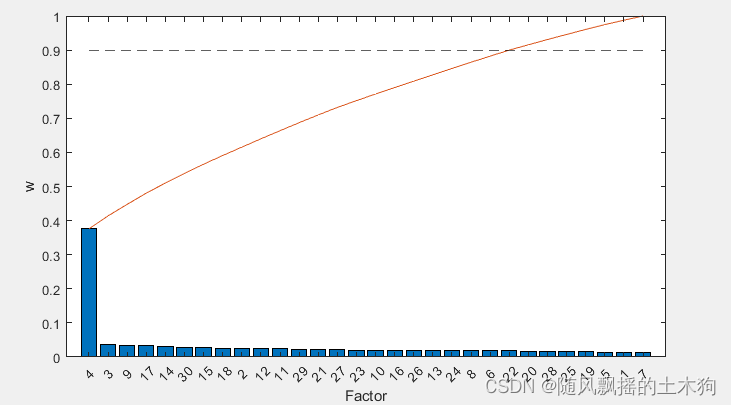
在这里插入图片描述

(5)自适应随机森林ARF

%% (5)自适应随机森林ARF
addpath('D:\小论文文件包最终版\基坑与算法文献\副业\特征排序\ARF')
ContributeRate=0.9;
params.RFLeaf=[5,10,20,50,100,200,500]; %RFLeaf定义初始的叶子节点个数，这里设置了从5到500。
params.Maxepoch=500; % 选择叶子节点个数对应的最大训练步数
[XT,RFModel,w,params]= myarf(data,ContributeRate,params);
xarf=data(:,XT);

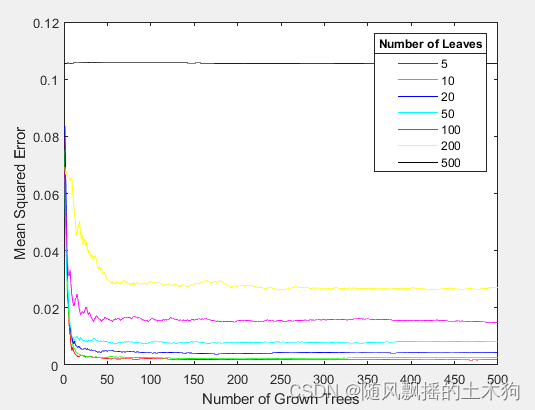
在这里插入图片描述
nTree = 470；nLeaf = 5；

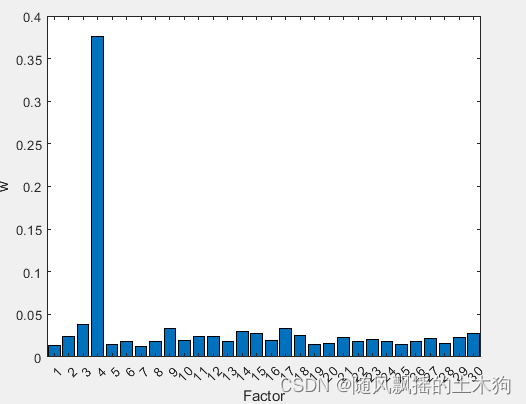
(6)皮尔逊相关系数PCC

%% (6)皮尔逊相关系数PCC
addpath('D:\特征排序\PCC')
ContributeRate=0.9;
xtrain =data(:,1:end-1);
ytrain =data(:,end);
opts.Nf =size(xtrain,2);    % 选择因素数量
FS     = mypcc(xtrain,ytrain,opts); % 皮尔逊相关系数法 函数调用
sf_idx = FS.sf;
 % 绘图  ，特征排序
extra()
 xpcc=yt(1:mm);%取前MM个数据

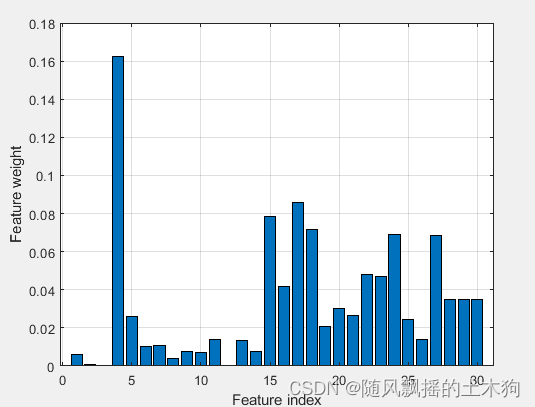
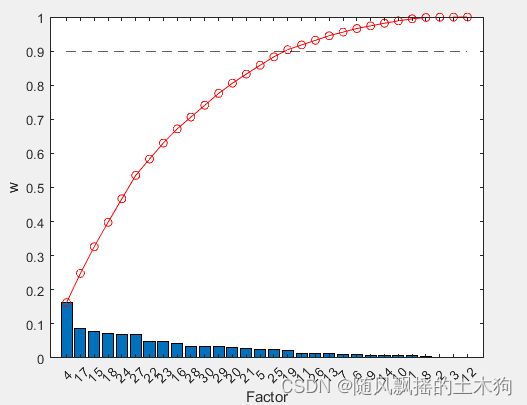
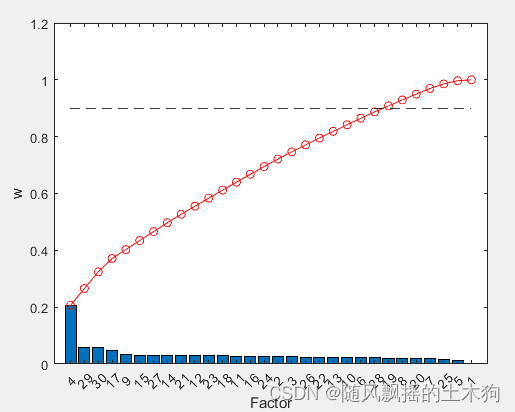
在这里插入图片描述

(7)Relief-F算法

%% (7)Relief-F算法
addpath('D:\特征排序\Relief-F')
ContributeRate=0.9;
xtrain =data(:,1:end-1);
ytrain =data(:,end);
opts.Nf =size(xtrain,2);    % 选择因素数量
FS     = myReliefF(xtrain,ytrain,opts); %  函数调用
sf_idx = FS.sf;
extra()
 xReliefF=yt(1:mm);%取前MM个数据

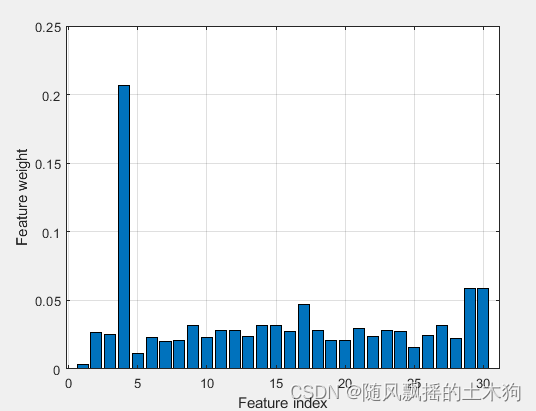
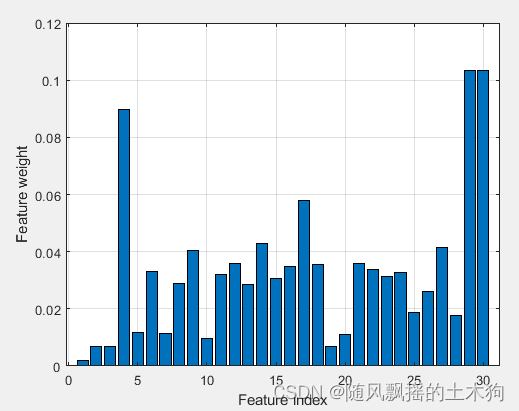
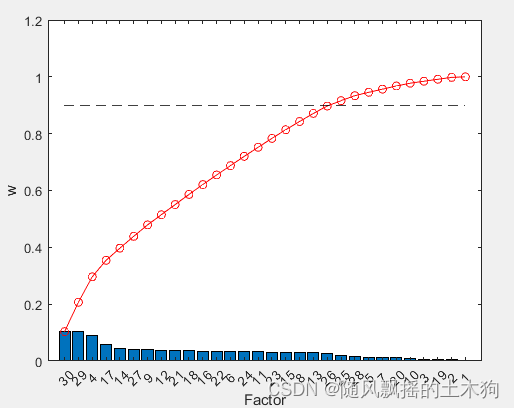
在这里插入图片描述

(8)Term Variance算法

%% (8)Term Variance算法
addpath('D:\特征排序\TV')
ContributeRate=0.9;
xtrain =data(:,1:end-1);
ytrain =data(:,end);
opts.Nf =size(xtrain,2);    % 选择因素数量
FS     = mytv(xtrain,ytrain,opts); %  函数调用
sf_idx = FS.sf;
extra()
 xTV=yt(1:mm);%取前MM个数据