目录
何为赫夫曼树?
赫夫曼树算法
赫夫曼编码
编程实现赫夫曼树
编程实现赫夫曼编码
编程实现WPL
总代码及分析
何为赫夫曼树?
树的路径长度:从树根到每一结点的路径长度之和
结点的带权路径长度:从树根到该结点的路径长度与结点上权的乘积
树的带权路径长度:树中所有叶子结点的带权路径长度之和

假设有n个权值(w1.w2,,,Wn),试构造一棵有n个叶子结点的二叉树,每个叶子结点带权为Wi,则其中WPL最小的二叉称做最优二叉树或赫夫曼树。
赫夫曼树算法
(1)根据给定的n个权值(w1,w2,…,Wn,)构成n棵二叉树的集合F=(T1,T2,…,Tn,其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树均空。
(2)在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
(3)在F中删除这两棵树,同时将新得到的二叉树加入F中。
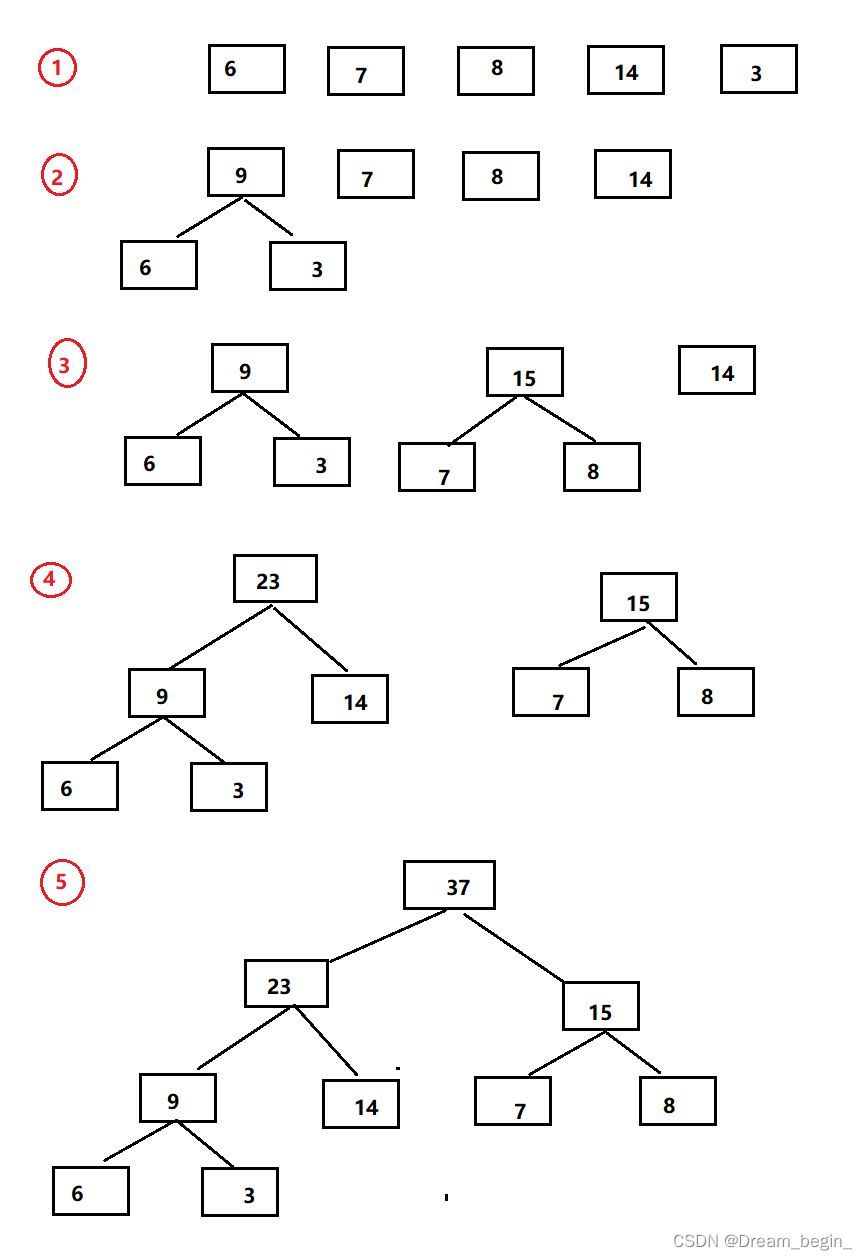
(4)重复(2)和(3),直到F只含一棵树为止。这棵树便是赫夫曼树。
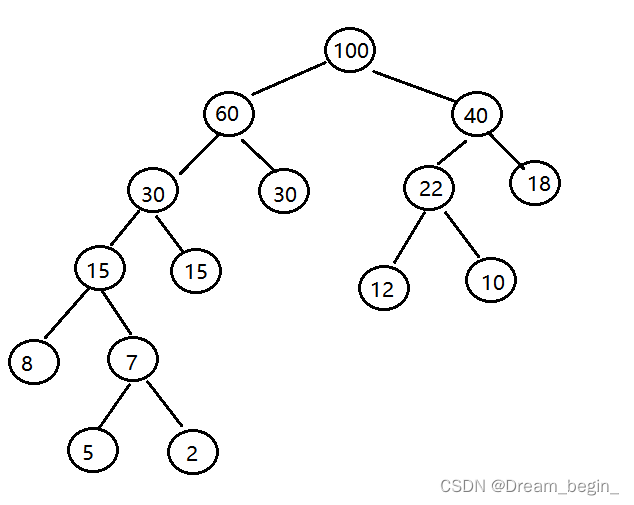
如下图:
赫夫曼编码
设一课二叉树为:
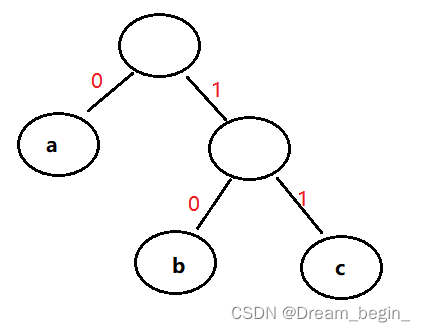
其3个叶子结点分别表示a、b、c3个字符, 约定左分支表示字符‘0’,右分支表示字符‘1’。则可以从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码。如上图可以得到a、b、c的二级制前缀编码分别为:0、10、11。
如何得到使电文总长最短的二级制编码?假设每种字符在电文中出现的次数为i,编码长度为j,而电文只有n种字符,则电文总长为n种i*j的和。对应到二叉树上,若i表示叶子结点的权值,j为从根到叶子的路径长度。则电文总长恰为二叉树带权路径长度。所以,设计电文总长最短的二级制前缀编码即以N种字符出现的频率作为权值,设计一颗赫夫曼树的问题
编程实现赫夫曼树
//哈夫曼树的存储表示
typedef struct
{
int weight; //节点的权值
int parent, lchild, rchild; //节点的双亲,左孩子和右孩子
} HTNode, * HuffmanTree;
typedef char** HuffmanCode;
//查权值最小且双亲为0的节点
void Select(HuffmanTree HT, int len, int& s1, int& s2)
{
int i, min1 = 0x3f3f3f3f, min2 = 0x3f3f3f3f; //先赋予最大值
for (i = 1; i <= len; i++)
{
if (HT[i].weight < min1 && HT[i].parent == 0)
{
min1 = HT[i].weight;
s1 = i;
}
}
int temp = HT[s1].weight; //将原值存放起来,然后先赋予最大值,防止s1被重复选择
HT[s1].weight = 0x3f3f3f3f;
for (i = 1; i <= len; i++)
{
if (HT[i].weight < min2 && HT[i].parent == 0)
{
min2 = HT[i].weight;
s2 = i;
}
}
HT[s1].weight = temp; //恢复原来的值
}
void CreatHuffmanTree(HuffmanTree& HT, int n,int*w)
{
//构造赫夫曼树HT
int m, s1, s2, i;
if (n <= 1)
return;
m = 2 * n - 1;
HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode)); //0号单元未用,所以需要动态分配m+1个单元,HT[m]表示根结点
for (i = 1; i <= m; ++i) //将1~m号单元中的权重、双亲、左孩子,右孩子的下标都初始化为0
{
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
HT[i].weight = 0;
}
for (i = 1; i <= n; ++i) //输入前n个单元中叶子结点的权值
{
HT[i].weight = *w;
w++;
}
/*――――――――――初始化工作结束,下面开始创建赫夫曼树――――――――――*/
for (i = n + 1; i <= m; ++i)
{ //通过n-1次的选择、删除、合并来创建赫夫曼树
Select(HT, i - 1, s1, s2);
//在HT[k](1≤k≤i-1)中选择两个其双亲域为0且权值最小的结点,
// 并返回它们在HT中的序号s1和s2
HT[s1].parent = i;
HT[s2].parent = i;//这里双亲不为0,相当于把s1和s2删除
//得到新结点i,从森林中删除s1,s2,将s1和s2的双亲域由0改为i
HT[i].lchild = s1;
HT[i].rchild = s2; //s1,s2分别作为i的左右孩子
HT[i].weight = HT[s1].weight + HT[s2].weight; //i 的权值为左右孩子权值之和
}
}编程实现赫夫曼编码
/*
从叶子节点到根节点逆向求赫夫曼树HT中n个叶子节点的赫夫曼编码,并保存在HC中
*/
void HuffmanCoding(HuffmanTree&HT, HuffmanCode& HC, int n)
{
//用来保存指向每个赫夫曼编码串的指针
HC = (HuffmanCode)malloc((n+1) * sizeof(char*));
if (!HC)
{
exit(-1);
}
//临时空间,用来保存每次求得的赫夫曼编码串
//对于有n个叶子节点的赫夫曼树,各叶子节点的编码长度最长不超过n-1
//外加一个'\0'结束符,因此分配的数组长度最长为n即可
char* code = (char*)malloc(n * sizeof(char));
if (!code)
{
printf("code malloc faild!");
exit(-1);
}
code[n - 1] = '\0'; //编码结束符,亦是字符数组的结束标志
//求每个字符的赫夫曼编码
int i;
for (i = 1; i <= n; i++)
{
int current = i; //定义当前访问的节点
int father = HT[i].parent; //当前节点的父节点
int start = n - 1; //每次编码的位置,初始为编码结束符的位置
//从叶子节点遍历赫夫曼树直到根节点
while (father !=0)
{
if (HT[father].lchild == current) //如果是左孩子,则编码为0
code[--start] = '0';
else //如果是右孩子,则编码为1
code[--start] = '1';
current = father;
father = HT[father].parent;
}
//为第i个字符的编码串分配存储空间
HC[i] = (char*)malloc((n - start) * sizeof(char));
if (!HC[i])
{
printf("HC[i] malloc faild!");
exit(-1);
}
//将编码串从code复制到HC
strcpy(HC[i], code + start);
}
for (int i = 1; i <=n; ++i) {
printf("%s\n", HC[i]);
}
free(code); //释放保存编码串的临时空间
}编程实现WPL
从叶子结点开始遍历二叉树直到根结点,根结点为HT[2n-1],且HT[2n-1].parent=0;
各叶子结点为HT[1]、HT[2]...HT[n]。
关键步骤是求出各个叶子结点的路径长度,用此路径长度*此结点的权值就是
此结点带权路径长度,最后将各个叶子结点的带权路径长度加起来即可。
int countWPL1(HuffmanTree HT, int n)
{
int i, countRoads, WPL = 0;
/*
由creat_huffmanTree()函数可知,HT[1]、HT[2]...HT[n]存放的就是各个叶子结点,
所以挨个求叶子结点的带权路径长度即可
*/
for (i = 1; i <=n; i++)
{
int father = HT[i].parent; //当前节点的父节点
countRoads = 0;//置当前路径长度为0
//从叶子节点遍历赫夫曼树直到根节点
while (father != 0)
{
countRoads++;
father = HT[father].parent;
}
WPL += countRoads * HT[i].weight;
}
return WPL;
}总代码及分析
#include <stdio.h>
#include<stdlib.h>
#include<string>
//哈夫曼树的存储表示
typedef struct
{
int weight; //节点的权值
int parent, lchild, rchild; //节点的双亲,左孩子和右孩子
} HTNode, * HuffmanTree;
typedef char** HuffmanCode;
//查权值最小且双亲为0的节点
void Select(HuffmanTree HT, int len, int& s1, int& s2)
{
int i, min1 = 0x3f3f3f3f, min2 = 0x3f3f3f3f; //先赋予最大值
for (i = 1; i <= len; i++)
{
if (HT[i].weight < min1 && HT[i].parent == 0)
{
min1 = HT[i].weight;
s1 = i;
}
}
int temp = HT[s1].weight; //将原值存放起来,然后先赋予最大值,防止s1被重复选择
HT[s1].weight = 0x3f3f3f3f;
for (i = 1; i <= len; i++)
{
if (HT[i].weight < min2 && HT[i].parent == 0)
{
min2 = HT[i].weight;
s2 = i;
}
}
HT[s1].weight = temp; //恢复原来的值
}
void CreatHuffmanTree(HuffmanTree& HT, int n,int*w)
{
//构造赫夫曼树HT
int m, s1, s2, i;
if (n <= 1)
return;
m = 2 * n - 1;
HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode)); //0号单元未用,所以需要动态分配m+1个单元,HT[m]表示根结点
for (i = 1; i <= m; ++i) //将1~m号单元中的权重、双亲、左孩子,右孩子的下标都初始化为0
{
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
HT[i].weight = 0;
}
for (i = 1; i <= n; ++i) //输入前n个单元中叶子结点的权值
{
HT[i].weight = *w;
w++;
}
/*――――――――――初始化工作结束,下面开始创建赫夫曼树――――――――――*/
for (i = n + 1; i <= m; ++i)
{ //通过n-1次的选择、删除、合并来创建赫夫曼树
Select(HT, i - 1, s1, s2);
//在HT[k](1≤k≤i-1)中选择两个其双亲域为0且权值最小的结点,
// 并返回它们在HT中的序号s1和s2
HT[s1].parent = i;
HT[s2].parent = i;//这里双亲不为0,相当于把s1和s2删除
//得到新结点i,从森林中删除s1,s2,将s1和s2的双亲域由0改为i
HT[i].lchild = s1;
HT[i].rchild = s2; //s1,s2分别作为i的左右孩子
HT[i].weight = HT[s1].weight + HT[s2].weight; //i 的权值为左右孩子权值之和
}
} // CreatHuffmanTree
/*
从叶子节点到根节点逆向求赫夫曼树HT中n个叶子节点的赫夫曼编码,并保存在HC中
*/
void HuffmanCoding(HuffmanTree&HT, HuffmanCode& HC, int n)
{
//用来保存指向每个赫夫曼编码串的指针
HC = (HuffmanCode)malloc((n+1) * sizeof(char*));
if (!HC)
{
exit(-1);
}
//临时空间,用来保存每次求得的赫夫曼编码串
//对于有n个叶子节点的赫夫曼树,各叶子节点的编码长度最长不超过n-1
//外加一个'\0'结束符,因此分配的数组长度最长为n即可
char* code = (char*)malloc(n * sizeof(char));
if (!code)
{
printf("code malloc faild!");
exit(-1);
}
code[n - 1] = '\0'; //编码结束符,亦是字符数组的结束标志
//求每个字符的赫夫曼编码
int i;
for (i = 1; i <= n; i++)
{
int current = i; //定义当前访问的节点
int father = HT[i].parent; //当前节点的父节点
int start = n - 1; //每次编码的位置,初始为编码结束符的位置
//从叶子节点遍历赫夫曼树直到根节点
while (father !=0)
{
if (HT[father].lchild == current) //如果是左孩子,则编码为0
code[--start] = '0';
else //如果是右孩子,则编码为1
code[--start] = '1';
current = father;
father = HT[father].parent;
}
//为第i个字符的编码串分配存储空间
HC[i] = (char*)malloc((n - start) * sizeof(char));
if (!HC[i])
{
printf("HC[i] malloc faild!");
exit(-1);
}
//将编码串从code复制到HC
strcpy(HC[i], code + start);
}
for (int i = 1; i <=n; ++i) {
printf("%s\n", HC[i]);
}
free(code); //释放保存编码串的临时空间
}
/*
从叶子结点开始遍历二叉树直到根结点,根结点为HT[2n-1],且HT[2n-1].parent=0;
各叶子结点为HT[1]、HT[2]...HT[n]。
关键步骤是求出各个叶子结点的路径长度,用此路径长度*此结点的权值就是
此结点带权路径长度,最后将各个叶子结点的带权路径长度加起来即可。
*/
int countWPL1(HuffmanTree HT, int n)
{
int i, countRoads, WPL = 0;
/*
由creat_huffmanTree()函数可知,HT[1]、HT[2]...HT[n]存放的就是各个叶子结点,
所以挨个求叶子结点的带权路径长度即可
*/
for (i = 1; i <=n; i++)
{
int father = HT[i].parent; //当前节点的父节点
countRoads = 0;//置当前路径长度为0
//从叶子节点遍历赫夫曼树直到根节点
while (father != 0)
{
countRoads++;
father = HT[father].parent;
}
WPL += countRoads * HT[i].weight;
}
return WPL;
}
int main()
{
HuffmanTree HT;
HuffmanCode HC;
int n;
printf("请输入叶子结点的个数:\n");
scanf("%d", &n);
int w[8] = { 2, 15, 30, 8, 10, 5, 12, 18 };
CreatHuffmanTree(HT, n,w);
printf("哈夫曼树建立完毕!\n");
printf("各字符赫夫曼编码为:\n");
HuffmanCoding(HT, HC, n);
printf("带权路径最小为:\n");
printf("%d", countWPL1(HT, n));
}测试:
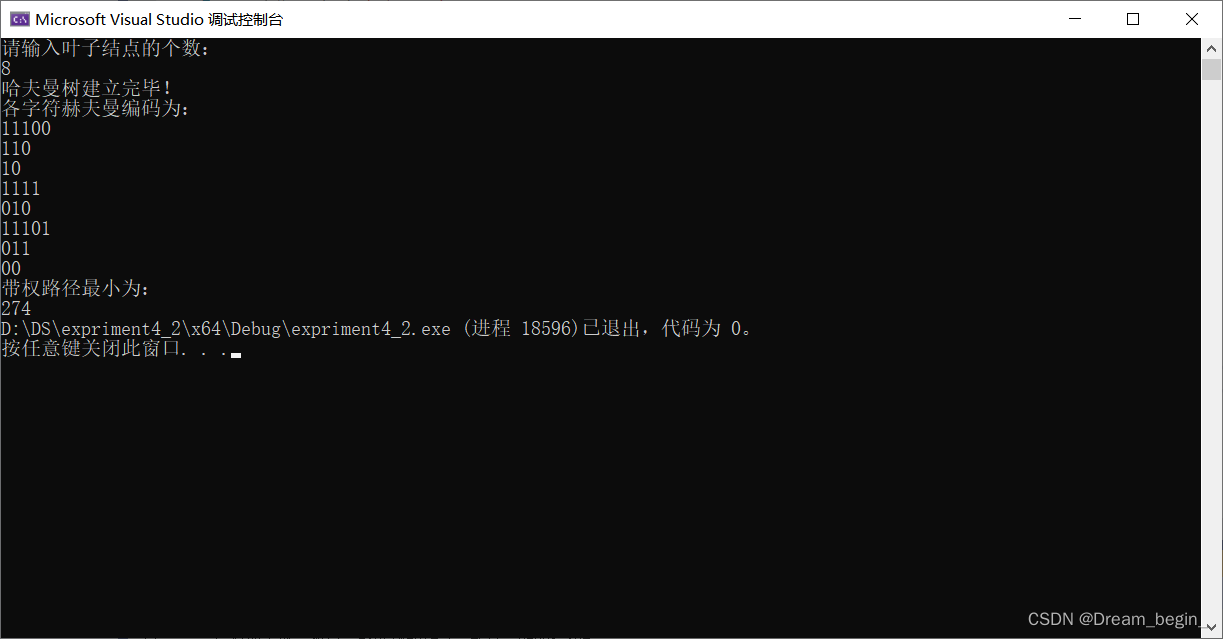
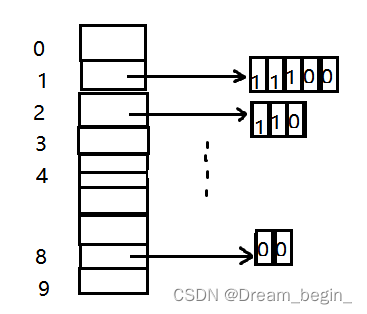
测试中的数据结构:
HT:
初始化后

创建后:

HC