红黑树（小白教学）

news2025/1/31 11:20:12

分享一个动画展示的网址：Red/Black Tree Visualization (lerogo.com)

将红黑树之前，我们先来了解一下什么叫做2-3树！！！

在我们以前学习的过程中（二分搜索树、完全二叉树等）结点都是存放了一个元素，2、3树中结点可以存放一个元素或者两个元素

因此每个结点都有2个或者3个孩子，这种的树叫做2-3树

重要性质：

1.2-3树是一棵绝对平衡的树

2.添加操作时永远不会添加到空的位置上去，根结点除外

下面给大家演示2-3树的添加操作过程（以上面的图为例）：

添加42

添加37

添加12

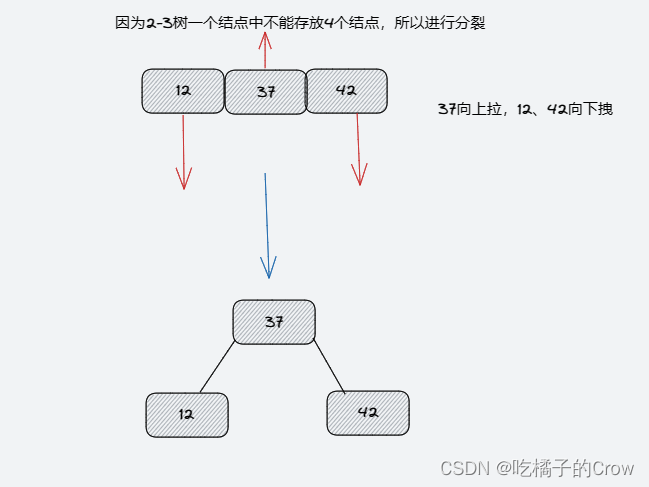
添加18

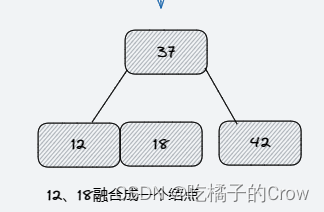
添加6

添加11

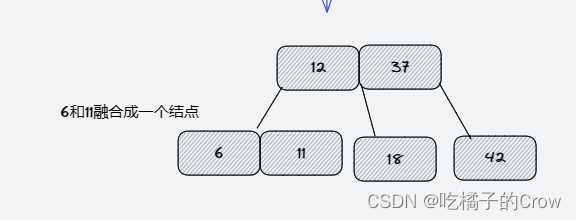
添加5

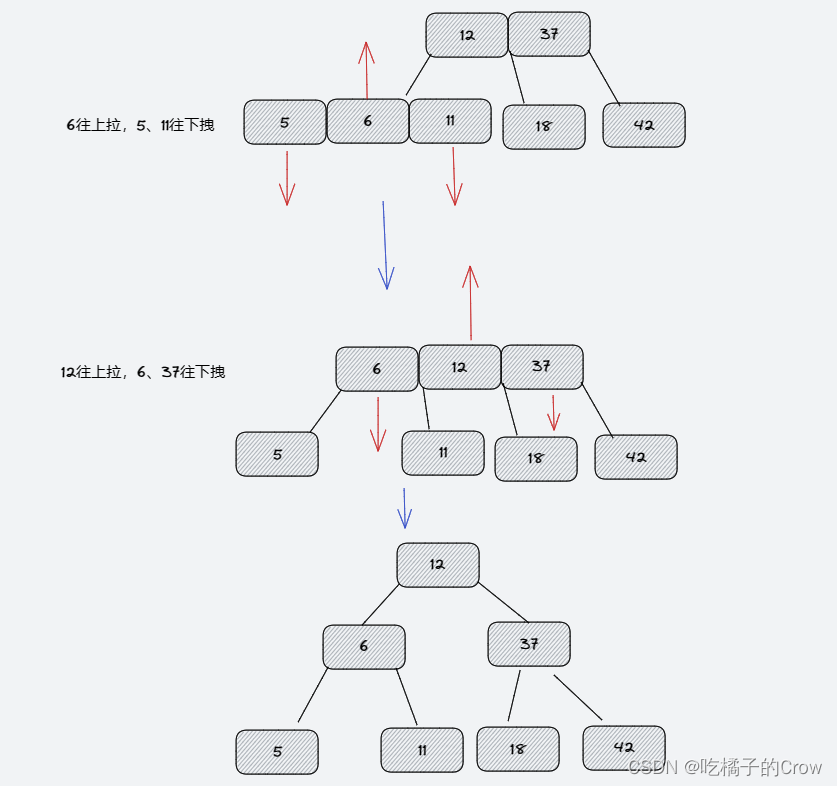
红黑树与2-3树的等价性：

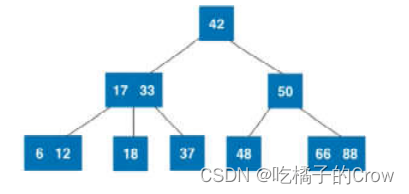
我们现在将这个2-3树转换为红黑树，如图所示：

从上图中我们可以得到红黑树的以下性质：

内个结点要么是红色、要么是黑色
红黑树的根节点一定是黑色的
每个叶子结点（最后的空节点）是黑色的
红色结点的左右孩子一定为黑色
任意结点到叶子结点中所经历的黑色结点的个数相同

注意：

1.严格意义上来讲，红黑树不是平衡二叉树，而是保持“黑平衡”的二叉树

2.时间复杂度为O(logn)

下面附构造红黑树的源代码：

public class RbTree<T extends Comparable<T>> {
    private class Node<T>{
        T val;
        Node left;
        Node right;
        int count;
        //节点的颜色
        boolean isRed;

        public Node(T val){
            this.val=val;
            this.left=this.right=null;
            this.isRed=true;//新创建的结点颜色为红色的（有可能是融合结点）
            this.count=1;
        }
    }
    //根节点
    private Node<T> root;
    private int size;

    //判断是否为空
    public boolean isEmpty(){
        return this.size==0;
    }
    //获取结点的个数
    public int getSize(){
        return this.size;
    }

    //添加元素
    public void add(T val){
        this.root=add(this.root,val);
        //更新根节点颜色
        this.root.isRed=false;
    }

   //左旋
    public Node leftRotate(Node node){
        Node x=node.right;
        node.right=x.left;
        x.left=node;
        //旋转结点的颜色等于原结点的颜色
        x.isRed=node.isRed;
        //原结点的颜色设为红色
        node.isRed=true;
        return x;
    }

    //右旋
    public Node rightRotate(Node node){
        Node x=node.left;
        node.left=x.right;
        x.right=node;
        x.isRed=node.isRed;
        node.isRed=true;
        return x;
    }

    //颜色反转
    public void flipColor(Node node){
        node.left.isRed=node.right.isRed=false;
        node.isRed=true;
    }

    //获取结点颜色的方法
    public boolean getColor(Node node){
        if(node==null){
            return false;
        }
        return node.isRed;
    }

    private Node add(Node<T> node,T val){
      //递归到底
        if(node==null){
            this.size++;
            return new Node(val);
        }
        Node result=null;
        //如果结点的值大于val,则在该节点的左树上找，返回的根节点直接挂接在该节点的左数上
        if(node.val.compareTo(val)>0){
           node.left= add(node.left,val);
        } else if(node.val.compareTo(val)<0){
            node.right=add(node.right,val);
        }else{
            node.count++;
        }
        result=node;

        //对结果进行处理
        //左旋   当根结点右结点为红色，左结点为黑色时，进行左旋
        if(getColor(result.right)&&!getColor(result.left)){
            result=leftRotate(result);
        }
        //右旋  当根结点的左节点为红，左节点的左节点为红时，进行右旋
        if(getColor(result.left)&&getColor(result.left.left)){
            result=rightRotate(result);
        }
        //颜色反转   当根节点的左右子树都为红时，进行颜色反转
        if(getColor(result.left)&&getColor(result.right)){
            flipColor(result);
        }
       return result;

    }
    //层序遍历
    public void levelTraversal() {
        if(this.root==null){
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(this.root);
        while (!queue.isEmpty()) {
            Node node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }

    }

在红黑树时，左旋与右旋操作：

右旋：

左旋：