312. 戳气球（困难）

在这里插入图片描述

解法一：动态规划

首先看一个区间：

在这里插入图片描述

区间(i,j) 是一个开区间，因为我们只能戳爆 i 和 j 之间的气球，不能戳爆索引为 i 和 j 的气球。

我们不妨考虑该区间内被戳爆的最后一个气球，索引记为 k。因为粉色气球是该区间内最后被戳爆的气球，所以在开区间 (i, j) 内除了它没有别的气球了，所以 DP 的状态转移方程只和 i 和 j 位置的数字有关。

在这里插入图片描述

状态定义

定义 dp[i][j] 表示开区间 (i, j) 内能够得到的最多金币。

状态转移方程

开区间 (i, j) 内得到的最多金币分为三部分：

dp[i][k]：开区间 (i, k) 内得到的最多金币；
nums[i] * nums[k] * nums[j] ：戳爆气球 k 可以得到的金币数量。
dp[k][j] ：开区间 (k, j) 内得到的最多金币;

因此最终的状态转移方程为：dp[i][j] = dp[i][k] + nums[i] * nums[k] * nums[j] + dp[k][j];

其中，k 的值可以从 (i, j) 之间任选，所以应该枚举所有的 k 值，选择最大值来更新 dp[i][j]。

之后，就从 (i,j) 开区间只有三个数字的时候开始计算，存储每个小区间可以得到的最多金币，然后慢慢扩展到更大的区间，利用小区间里已经算好的数字来算更大的区间。

因此，这道题的第一层遍历是按照区间长度（从3开始，因为我们设置了一个辅助数组，后面会详细解释），第二层遍历是按照左端点的索引，第三层索引是 k 的索引。

初始化

这里设置了一个辅助数字 temp ，用于处理边界问题，当只剩下一个气球的时候，此时的开区间左边界 i = 0，右边界 j = n+1 ，这两个位置是没有气球的，根据题意，当它们是数字为 1 的气球，所以将它们的值设置为 1 。

因此，我们的区间长度就扩大了 2。

所以，当 n = 1 时，区间长度从 3 开始考虑。

最终的返回结果

最后返回开区间(0, n+1) 内的最多金币。

代码

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> dp(n+2, vector<int>(n+2, 0));
        vector<int> temp(n+2);

        // 辅助数组
        temp[0] = temp[n+1] = 1;
        for(int i=0; i<n; ++i){
            temp[i+1] = nums[i];
        }
        // len表示开区间长度
        for(int len = 3; len <=n+2; len++){
            // i表示开区间的左端点(取不到 所以从0开始)
            for(int l=0; l<=n-len+2; l++){
                // 右端点为：r = l+len-1
                int r = l + len - 1;
                for(int k=l+1; k<r; ++k){
                    dp[l][r] = max(dp[l][r], dp[l][k] + temp[l]*temp[k]*temp[r] + dp[k][r]);
                }
            }
        }
        return dp[0][n+1];
    }
};

思考

阅读大佬解法的时候，发现了他使用了动态规划对例子进行分析，一步步得到答案，这个思路蛮值得我学习的：

在这里插入图片描述

解法二：分治法+记忆化搜索

其实理解完解法一之后，分治法的思想很好理解。

使用分治法时，我们应该考虑的核心问题是「如何用子问题的解来表示原问题的解」，我们把描述子问题的解与原问题的解之间的关系的表达式称为状态转移方程，这里和动态规划是一致的。毕竟，分治法就是分而治之，最后自底向上的合并过程就是动态规划的解决过程。

子问题的思考

按照一般的思路，首先思考能不能直接将[3, 1, 5, 8]直接分为类似于[3]、[1, 5, 8]这样两个子问题。这意味着，我们强行认为必须戳完 [3] 才能戳 [1, 5, 8]，或者戳完[1, 5, 8]才能戳[3]，显然这不科学。即这两个子问题之间产生了依赖。

如何消除依赖呢？我们一开始的想法是先假设第一个被戳爆的气球为x，则x两边的气球则产生了依赖；那我们假设不戳爆x，则x两边的气球就没有了依赖关系！这个气球x，我们可以放在最后戳爆它。

这样，对于[3, 1, 5, 8]，假设最后戳爆5，则问题就被划分为如下图所示的两个子问题和一个O(1)的问题。

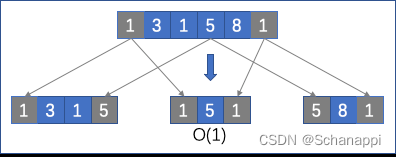
在这里插入图片描述

因此，分析到这里，和动态规划就相同了，要想求得大数组的最优解，就必须求得左右两个小数组的最优解。不同的是，在分治法中，我们使用递归来实现。

一样地，也需要遍历开区间（i，j）内的每一个气球，作为最后戳爆的气球。

即：ans = max(ans, maxsubCoins(temp, begin, k, cache) + temp[begin]*temp[k]*temp[end] + maxsubCoins(temp, k, end, cache));

此外，增加 cache 数组保存已经计算过的区间的最优解，避免重复计算。

问题

由于参考的代码是 java，转变成我自己的代码会超时，一直没办法解决，因此正确代码请见参考资料。

代码

// 超时
class Solution {
public:
    int maxsubCoins(vector<int>& temp, int begin, int end, vector<vector<int>> cache){
        // 说明剩下的两个气球相邻 无法戳破
        if(begin + 1 == end){
            return 0;
        }

        // 在缓存中查找，避免重复计算
        if(cache[begin][end] != 0){
            return cache[begin][end];
        }
        int ans = 0;
        // 找不到，开始计算
        for(int k=begin+1; k<end; ++k){
            ans = max(ans, maxsubCoins(temp, begin, k, cache) + temp[begin]*temp[k]*temp[end] + maxsubCoins(temp, k, end, cache));
        }
        cache[begin][end] = ans;
        return ans;
    }
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> cache(n+2, vector<int>(n+2, 0));
        // 辅助数组的写法2
        nums.insert(nums.begin(),1);
        nums.push_back(1);
        return maxsubCoins(nums, 0, n+1, cache);
    }
};