1.图像模糊

图像模糊是图像处理中最简单和常用的操作之一。

⚠️使用该操作的原因之一是为了给图像预处理时降低噪声。

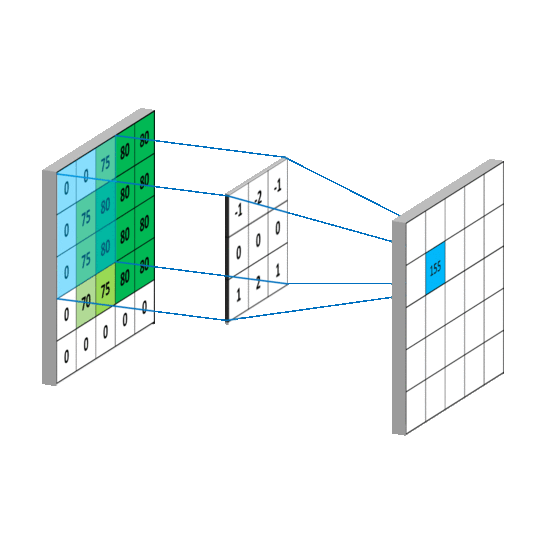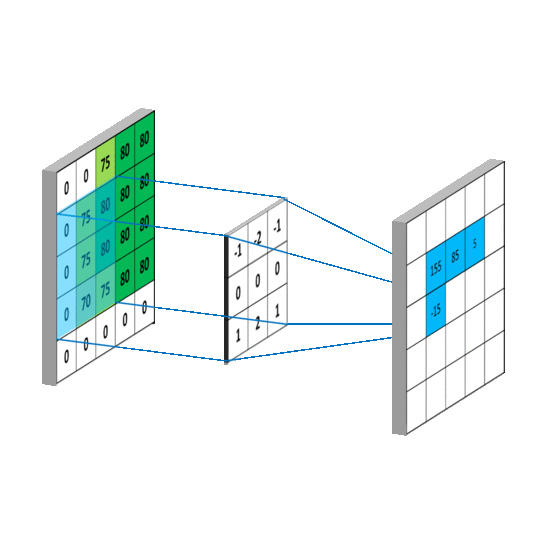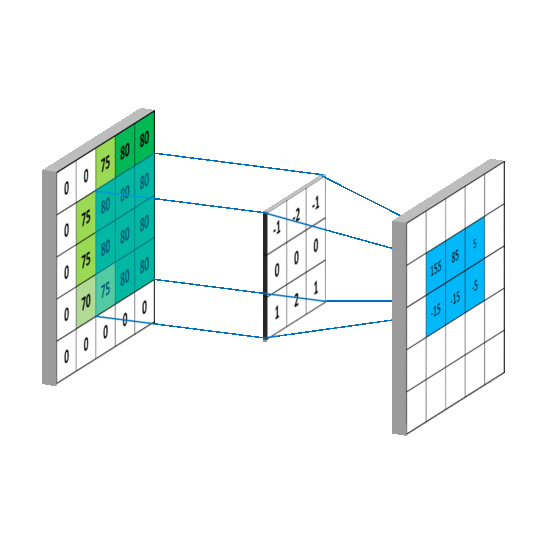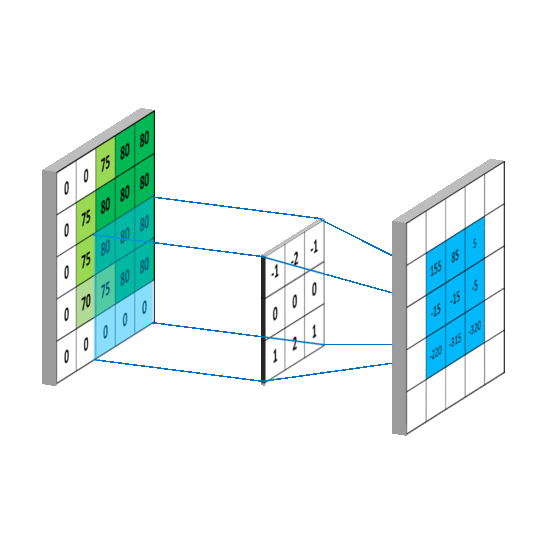
图像模糊操作背后是数学的卷积计算。

卷积操作的原理：

常用的图像模糊的方法：

1. 均值模糊
2. 高斯模糊
3. 中值模糊
4. 双边模糊

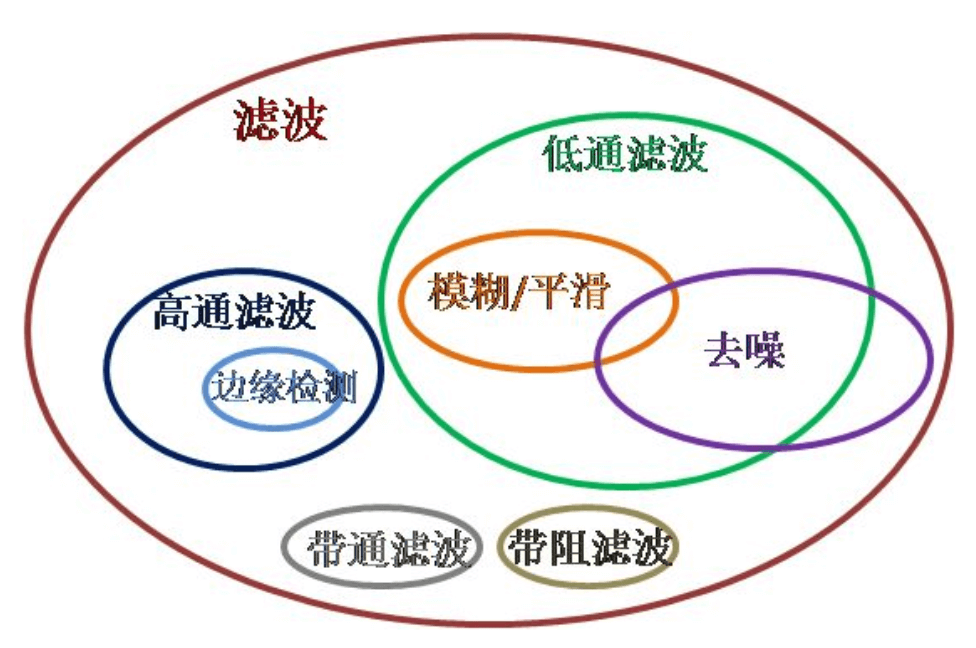
这四种模糊方式有时也被称为：均值滤波、高斯滤波、中值滤波和双边滤波。因为模糊属于一种滤波操作，具体关系可参照下图：

其中，均值滤波、高斯滤波和中值滤波属于线性滤波；而双边滤波属于非线性滤波。

接下来我们结合OpenCV中的相关API来进一步了解这些图像模糊的方法。

2.均值模糊

均值模糊的卷积核为：

kernel=1kernelwidth×kernelheight⎡⎣⎢⎢1⋮1⋯⋱⋯1⋮1⎤⎦⎥⎥

卷积核亦称掩膜。

OpenCV中的API：

1
2
3
4
5
6
7

void blur(
	InputArray src,
	OutputArray dst,
	Size ksize,
	Point anchor=Point(-1,-1),
	int borderType = BORDER_DEFAULT
);

部分参数解释：

1. 参数Size ksize表示卷积核的大小。Size(3,3)表示3×3

的核大小；Size(5,5)表示5×5

1. 的核大小。边长必须是正奇数。
2. 参数Point anchor表示锚点(anchor)的位置，即被平滑的那个点。默认值Point(-1,-1)表示锚点位于核的中心。

现在我们看下原图进行均值模糊之后的结果（左侧为原图，右侧为均值模糊后的图）：

1

blur(src,src_blur,Size(5,5),Point(-1,-1));

3.高斯模糊

3.1.高斯模糊的原理

高斯模糊所用的卷积核就是基于二维高斯分布生成的。

二维高斯分布见本文第6部分。

在高斯模糊中，二维高斯分布公式中的x1,x2

对应一个点的x,y坐标。因此可以假设x1,x2

是相互独立的，所以：

Cov(x1,x2)=Cov(x2,x1)=E(x1x2)−E(x1)E(x2)=E(x1)E(x2)−E(x1)E(x2)=0

并且：

Cov(x1,x1)=E(x21)−E2(x1)=σ21

同理：

Cov(x2,x2)=σ22

代入协方差矩阵∑

：

∑=[Cov(x1,x1)Cov(x2,x1)Cov(x1,x2)Cov(x2,x2)]=[σ2100σ22]

求其行列式：

∣∑∣=σ21σ22

则二维高斯分布公式可简化为：

f(x¯)=1(2π)(σ21σ22)1/2e−12[(x1−μ1σ1)2+(x2−μ2σ2)2]

假设我们要生成一个3×3

的高斯掩膜，锚点的坐标设置为(0,0)，则周边点的坐标为：

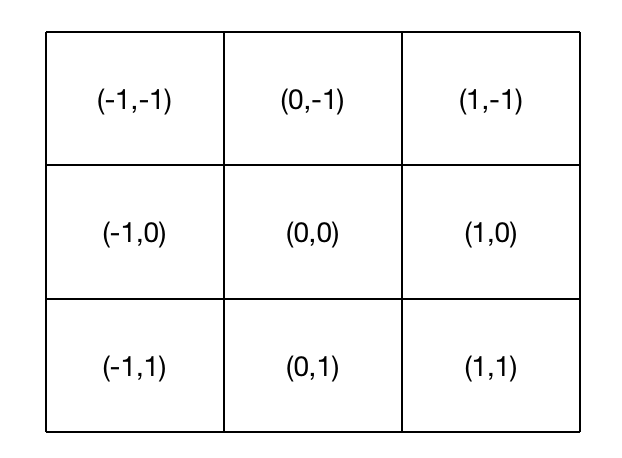
将(x1,x2)

对应的值代入上述公式中即可求得高斯掩膜。

为了方便，我们这里假设μ1=μ2=0,σ1=σ2=1

，又因为系数12π

为常数，因此可以省略，将二维高斯分布公式简化为：

e−12(x21+x22)

据此可得到：

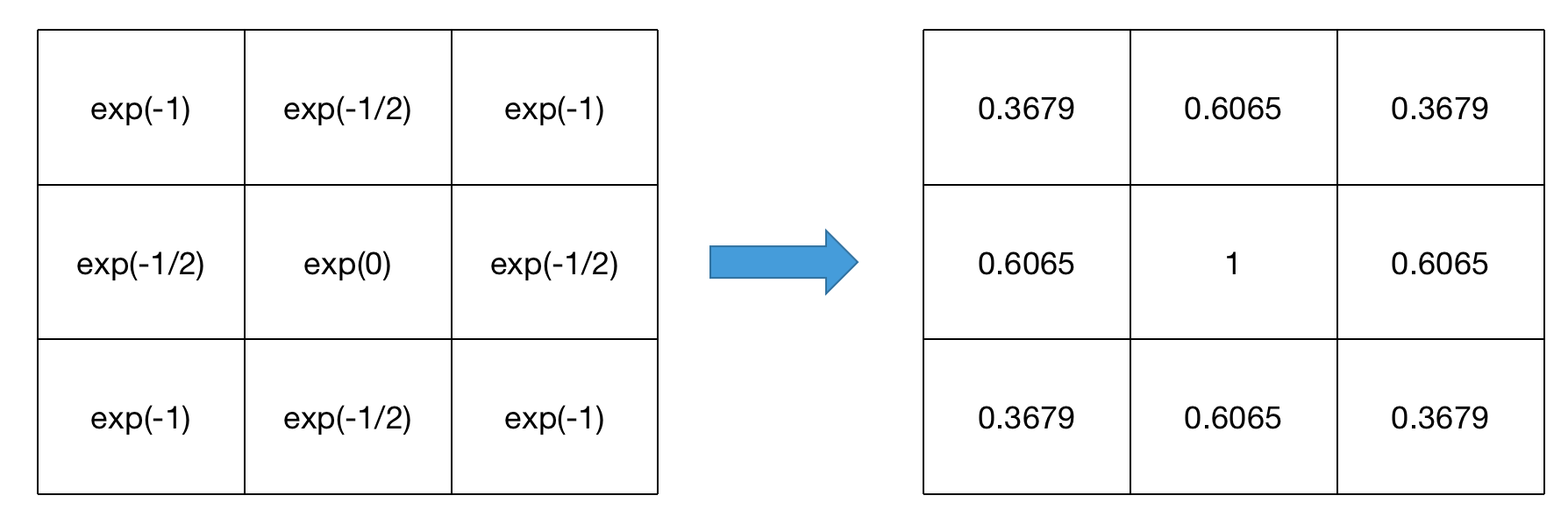
这9个点的权重总和不等于1，所以需要对其进行归一化处理：每个格子的数除以所有格子的数加起来的总和。这样即可得到一个3×3

的高斯掩膜：

3.2.高斯模糊的API

1
2
3
4
5
6
7
8

void GaussianBlur(
	InputArray src,
	OutputArray dst,
	Size ksize,
	double sigmaX,
	double sigmaY = 0,
	int borderType = BORDER_DEFAULT
);

其中，参数Size ksize表示卷积核的大小。sigmaX（高斯核在x方向的标准差）和sigmaY（高斯核在y方向的标准差）对应二维高斯分布公式中的σ1,σ2

。

如果σ

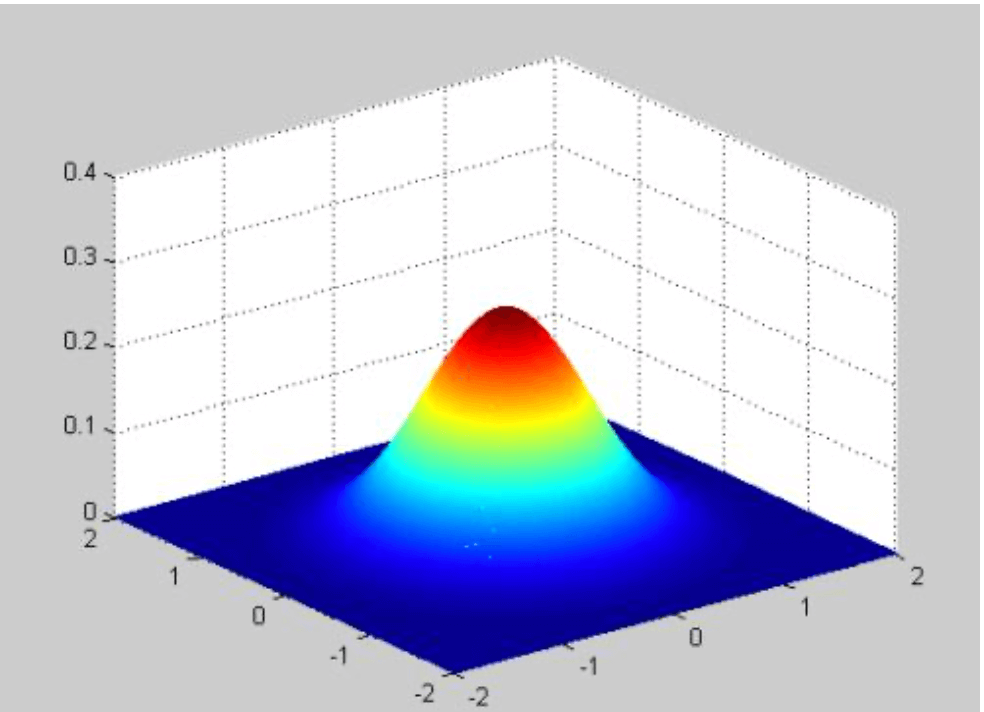
较小（其二维高斯分布概率密度函数图像见下图右），那么生成的掩膜的中心系数较大，而周围的系数较小，这样对图像的模糊效果就不是很明显；反之，σ

较大（其二维高斯分布概率密度函数图像见下图左），则生成的模版的各个系数相差就不是很大，比较类似均值模糊，对图像的模糊效果比较明显。

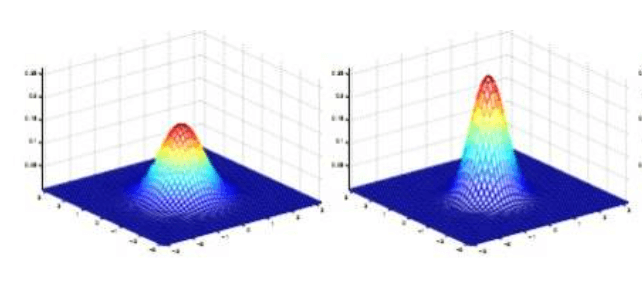
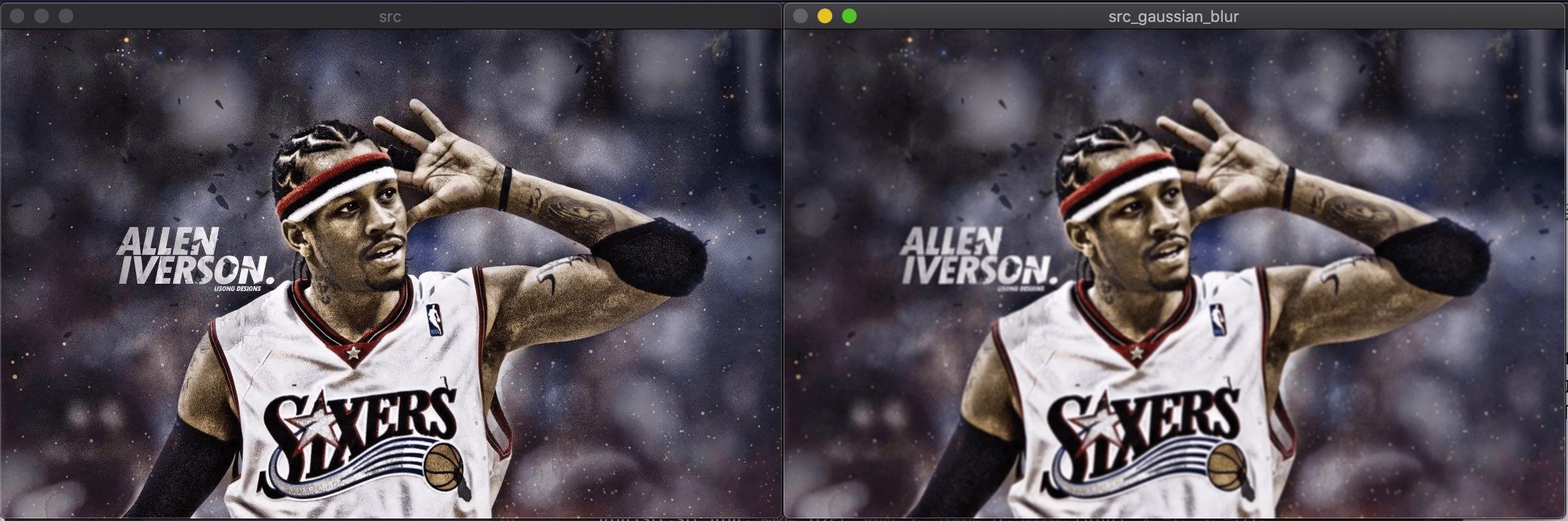
实际应用看下对比效果（左侧为原图，右侧为高斯模糊后的图）：

1

GaussianBlur(src,src_gaussian_blur,Size(5,5),3,3);

4.中值模糊

中值模糊即用中位数填补中心像素。

中值滤波的扩展：最小值滤波、最大值滤波。

中值模糊对椒盐噪声有很好的抑制作用。

椒盐噪声：也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，也可能是亮的区域有黑色像素或是在暗的区域有白色像素（或者两者皆有）。

中值模糊的API：

1
2
3
4
5

void medianBlur(
	InputArray src,
	OutputArray dst,
	int ksize
);

参数int ksize表示核的大小，必须大于1而且必须是奇数。

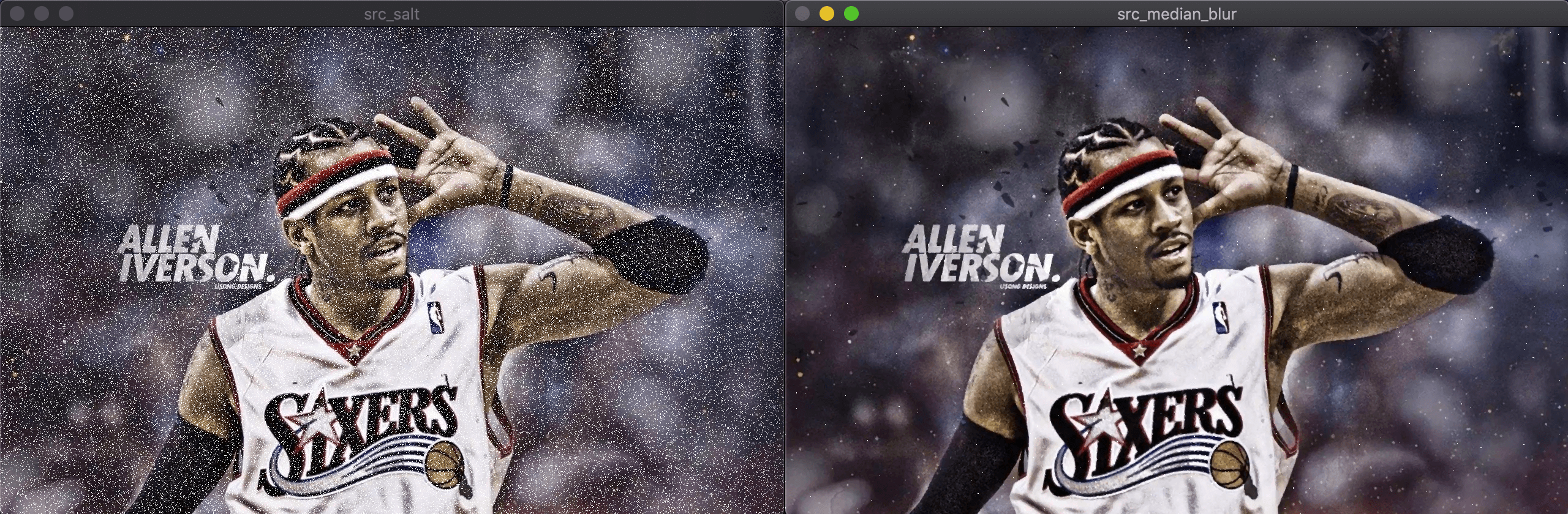
结果对比见下（左侧为加了椒盐噪声的原图，右侧为中值模糊后的图）：

1

medianBlur(src_salt,src_median_blur,3);

5.双边模糊

均值模糊无法克服边缘像素信息丢失缺陷，原因是均值滤波是基于平均权重。

高斯模糊部分克服了该缺陷，但是无法避免，因为没有考虑像素值的不同。

高斯双边模糊是边缘保留的滤波方法，避免了边缘信息丢失，保留了图像轮廓不变（边缘指的是物体的边缘、轮廓）。

5.1.双边模糊的原理

⚠️双边滤波器综合了高斯滤波器和α

截尾均值滤波器的特点。高斯滤波器只考虑像素间的欧式距离，其使用的模版系数随着和窗口中心的距离增大而减小；α截尾均值滤波器则只考虑了像素灰度值之间的差值，去掉α

%的最小值和最大值后再计算均值。

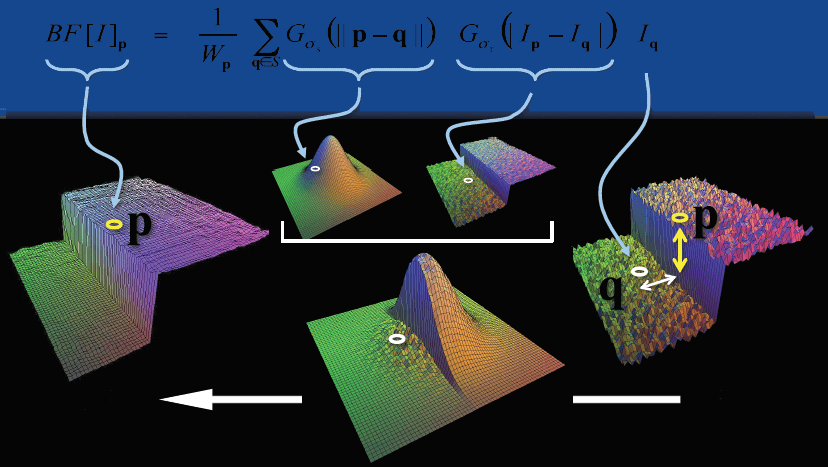
‼️双边滤波器就等于空间距离与灰度距离的乘积。其使用二维高斯函数生成距离模版，使用一维高斯函数生成值域模版（以下公式都省去了前面的系数）。

👉距离模版系数的生成公式如下：

d(i,j,k,l)=exp(−(i−k)2+(j−l)22σ2d)

这个公式和3.1部分中的公式其实是一样的。只不过省去了系数，并且假定σ1=σ2=σd

。(k,l)为模版窗口的中心坐标，通常为(0,0)，也就是(μ1,μ2)。(i,j)为模版窗口的其他系数的坐标，即(x1,x2)

。

👉值域模版系数的生成公式如下：

r(i,j,k,l)=exp(−∥f(i,j)−f(k,l)∥22σ2r)

其中，f(x,y)

表示图像在点(x,y)处的像素值；(k,l)为模版窗口的中心坐标；(i,j)为模版窗口的其他系数的坐标；σ2r

为高斯函数的方差。

将上述两个模版相乘就得到了双边滤波器的模版：

w(i,j,k,l)=d(i,j,k,l)∗r(i,j,k,l)=exp(−(i−k)2+(j−l)22σ2d−∥f(i,j)−f(k,l)∥22σ2r)

双边滤波也可以用下图表示，对P点进行模糊，Q点的距离虽然很近，但是像素值差距过大，所以Q点的权重很小，不会过多的考虑到Q点的信息，所以说双边滤波考虑到了边缘信息，避免了边缘信息的丢失。

5.2.双边模糊的API

1
2
3
4
5
6
7
8

void bilateralFilter(
	InputArray src,
	OutputArray dst,
	int d,
	double sigmaColor,
	double sigmaSpace,
	int borderType=BORDER_DEFAULT
);

部分参数解释：

1. int d是计算直径，范围内的像素都会被纳入计算。如果这个值我们设其为非正数，那么OpenCV会从第五个参数sigmaSpace来计算出它来。
2. double sigmaColor即为公式中的σr

• 。这个参数的值越大，就表明该像素邻域内有更宽广的颜色会被混合到一起。
• double sigmaSpace即为公式中的σd

1. 。数值越大，意味着越远的像素会相互影响。

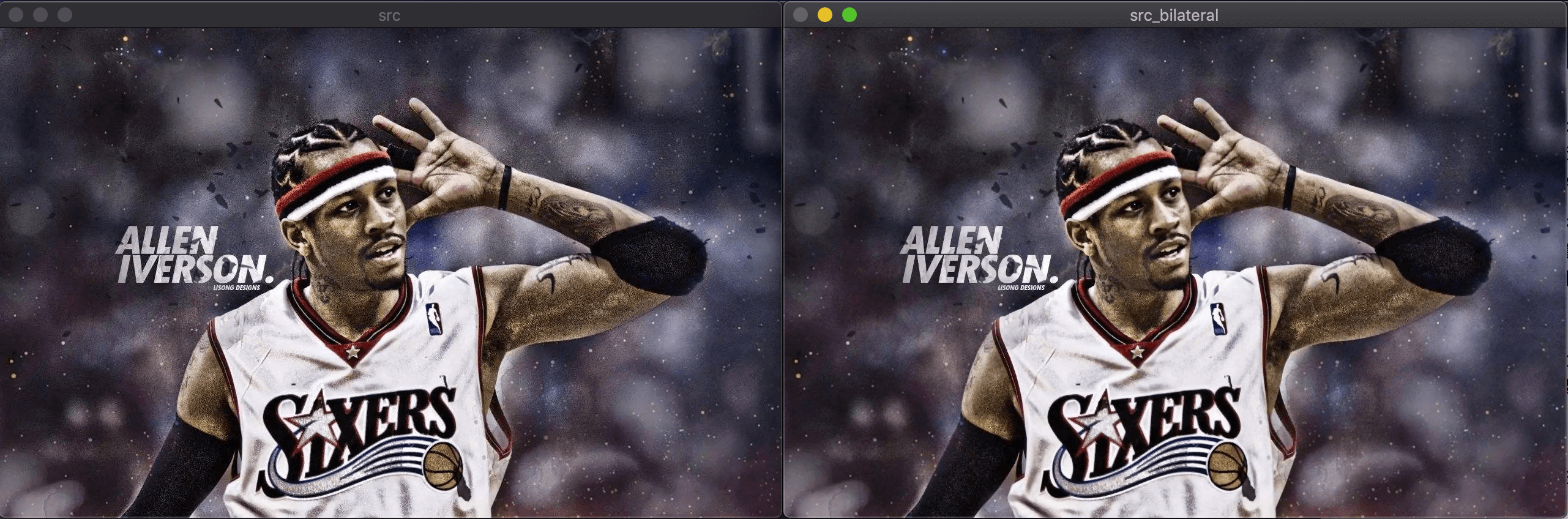
其效果见下（左侧为原图，右侧为双边模糊后的图）：

1

bilateralFilter(src,src_bilateral,3,100,3);

6.高斯分布

高斯分布(Gaussian distribution)又名正态分布。

👉一维高斯分布的概率密度函数为：

f(x)=12π−−√σe−(x−μ)22σ2

👉高维高斯分布的概率密度函数为：

f(x¯)=1(2π)D/21∣∑∣1/2e−12(x¯−μ¯)T∑−1(x¯−μ¯)

其中，x¯

表示维度为D的向量，μ¯则是这些向量的平均值，∑表示所有向量x¯的协方差矩阵，∣∑∣

表示协方差矩阵的行列式。

因此根据高维高斯分布的公式，我们可以得到二维高斯分布的概率密度函数为：

f(x¯)=1(2π)∣∑∣1/2e−12[(x1−μ1σ1)2+(x2−μ2σ2)2]

二维高斯分布的图像为：

7