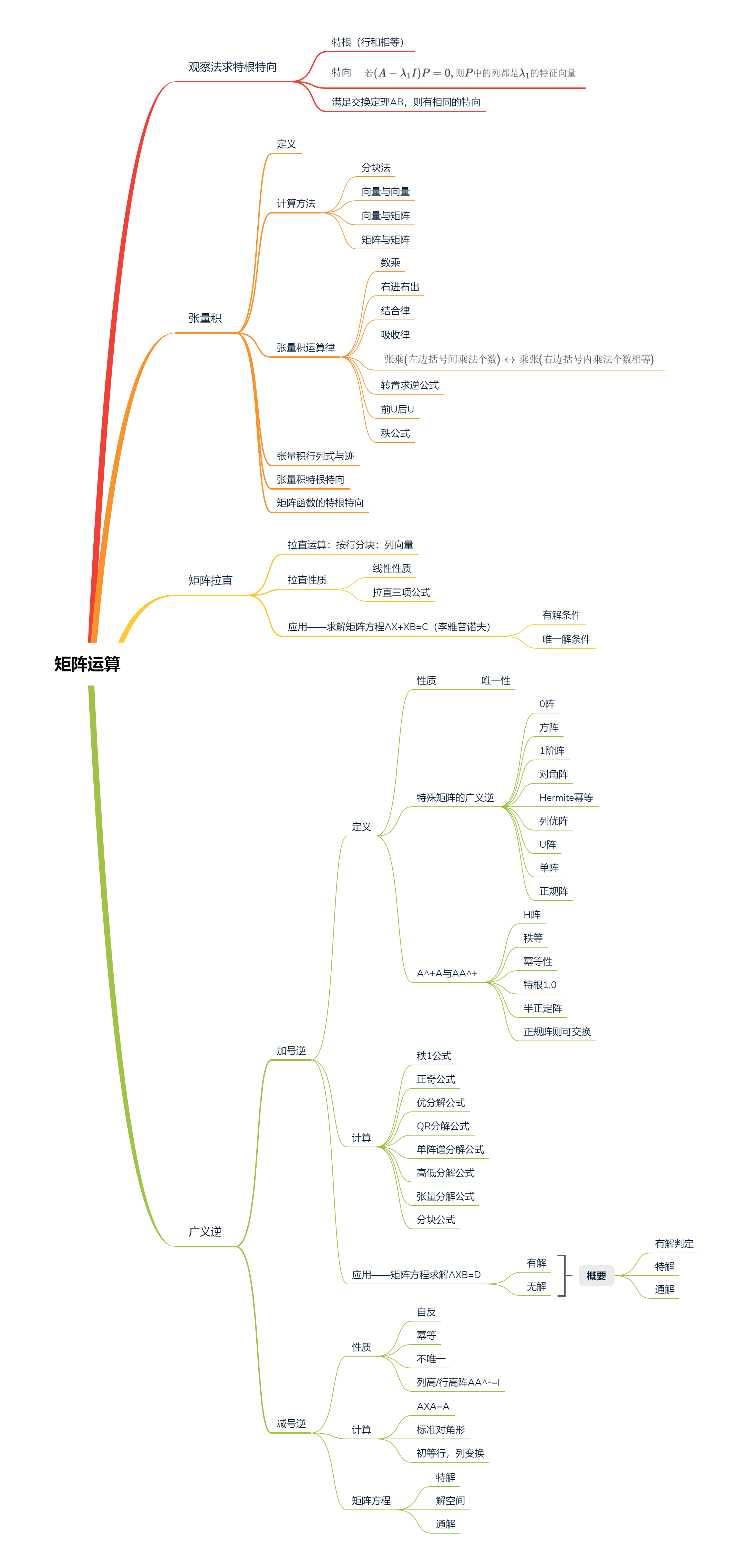
4.5 减号逆
若 A = A m × n A=A_{m\times n} A=Am×n 与 X = X n × m X=X_{n\times m} X=Xn×m ,有 A X A = A AXA=A AXA=A ,则称 X = X n × m X=X_{n\times m} X=Xn×m 为A的减号逆(一号逆),记为 X = A − = A ( 1 ) X=A^{-}=A^{(1)} X=A−=A(1)
全体 A − A^{-} A− 的集合记为 A { 1 } = { X ∣ A X A = A } A^{\{1\}}=\{X\mid AXA=A\} A{1}={X∣AXA=A}
- A − ∈ A { 1 } A^{-}\in A^{\{1\}} A−∈A{1}
4.5.1 性质
自反性: A A − A = A AA^{-}A=A AA−A=A
幂等性:
(
A
−
A
)
2
=
A
−
A
(A^{-}A)^2=A^{-}A
(A−A)2=A−A ,且
(
A
A
−
)
2
=
A
A
−
(AA^{-})^2=AA^{-}
(AA−)2=AA− ,其中A是方阵
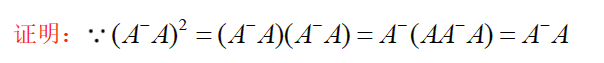
A − A^{-} A− 不唯一,可以看做 A − 1 A^{-1} A−1 的推广
- 如 A = ( 1 0 ) A=\left(\begin{matrix}1\\0\end{matrix}\right) A=(10) ,可取 X=(1 0) 或 Y=(1 1) 作为A的减号逆
- A − A^{-} A− 唯一的阵:方阵 A n × n A_{n\times n} An×n可逆,则必有唯一 A − 1 = A + = A − A^{-1}=A^{+}=A^- A−1=A+=A−
若A为列满秩(高阵),则 A − A = I A^-A=I A−A=I;若A为行满秩(低阵),则 A A − = I AA^-=I AA−=I

4.5.2 计算
a. 求解 A X A = A AXA=A AXA=A
求解减号逆 A − A{-} A− 即求解 A X A = A AXA=A AXA=A 的全体通解
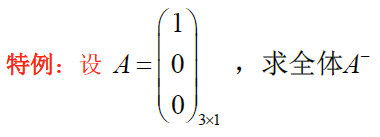 在这里插入图片描述
在这里插入图片描述
由 矩 阵 方 程 A X B = D 的 特 解 X 0 = A + = ( 1 , 0 , 0 ) , 故 通 解 为 A − = X = X 0 + Y − A + A Y A A + = ( 1 , 0 , 0 ) + ( a , b , c ) − ( a , 0 , 0 ) = ( 1 , b , c ) \begin{aligned} &由矩阵方程AXB=D的特解X_0=A^+=\left(1,0,0\right),故通解为A^-=X=X_0+Y-A^+AYAA^+\\ &=\left(1,0,0\right)+\left(\begin{matrix}a,b,c\end{matrix}\right)-\left(\begin{matrix}a,0,0\end{matrix}\right)=\left(\begin{matrix}1,b,c\end{matrix}\right) \end{aligned} 由矩阵方程AXB=D的特解X0=A+=(1,0,0),故通解为A−=X=X0+Y−A+AYAA+=(1,0,0)+(a,b,c)−(a,0,0)=(1,b,c)
也可见 A − A^- A− 不唯一
- 对于高阶阵 A − = A + + ( Y − A + A Y A A + ) A^-=A^++(Y-A^+AYAA^+) A−=A++(Y−A+AYAA+) 的计算比较复杂
b. 标准对角形
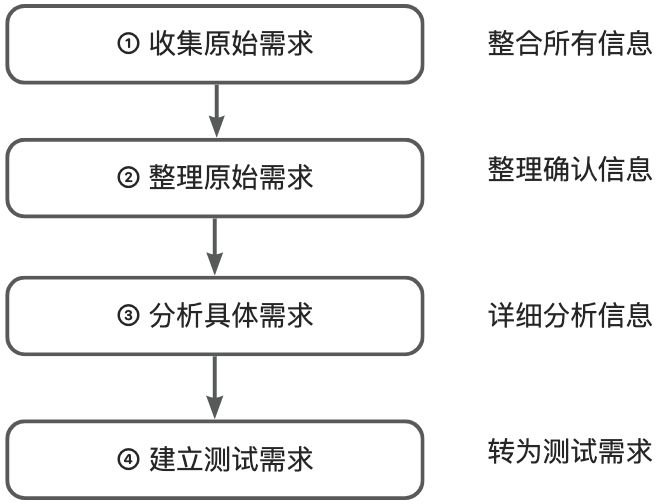
若 A = ( I r 0 0 0 ) m × n A=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n} A=(Ir000)m×n ,则全体 A − = ( I r B C D ) n × m A^-=\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m} A−=(IrCBD)n×m ,BCD为任一小块

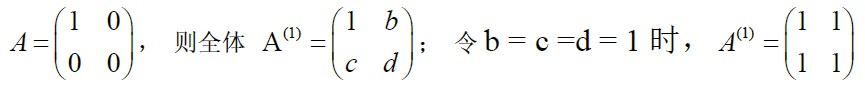
SP
若 P A Q = ( I r 0 0 0 ) m × n PAQ=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n} PAQ=(Ir000)m×n ,全体 A − = Q ( I r 0 0 0 ) n × m P A^{-}=Q\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{n\times m}P A−=Q(Ir000)n×mP ,BCD为任一小块
c. 初等行,列变换(一般方法)
设 A = A m × n A=A_{m\times n} A=Am×n ,令 ( A I m I n 0 ) → 列 变 换 行 变 换 ( ( I r 0 0 0 ) m × n P Q 0 ) \left(\begin{array}{c:c}A&I_m\\\hdashline I_n&0\end{array}\right)\xrightarrow[列变换]{行变换}\left(\begin{array}{c:c}\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}&P\\\hdashline Q&0\end{array}\right) (AInIm0)行变换列变换⎝⎛(Ir000)m×nQP0⎠⎞ ,则有 A − = Q ( I r B C D ) n × m P A^-=Q\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}P A−=Q(IrCBD)n×mP
eg

4.5.3 矩阵方程求解
前置知识:正规方程求解
a. 特解

b. 解空间
N ( A ) N(A) N(A) 或 A Y = 0 AY=0 AY=0 的通解为 Y = ( I n − A − A ) y Y=(I_n-A^-A)y Y=(In−A−A)y , ∀ y ∈ C n \forall y\in C^n ∀y∈Cn
N ( A ) = { Y ∣ A Y = 0 } N(A)=\{Y\vert AY=0\} N(A)={Y∣AY=0} , X = ( I n − A − A ) y , y = ( y 1 ⋮ y n ) ∈ C n X=(I_n-A^-A)y,y=\left(\begin{matrix}y_1\\\vdots\\y_n\end{matrix}\right)\in C^n X=(In−A−A)y,y=⎝⎜⎛y1⋮yn⎠⎟⎞∈Cn
设y的值域为 R,则 N ( A ) = R ( I n − A − A ) N(A)=R(I_n-A^-A) N(A)=R(In−A−A) ,维数 d i m N ( A ) = n − r ( A − A ) dim N(A)=n-r(A^-A) dimN(A)=n−r(A−A)
c. 通解