题目描述

ECDSA
签名
假设我们的私钥为 d A d_A dA而公钥为 Q A Q_A QA, Q A = d A ⋅ G Q_A=d_A\cdot G QA=dA⋅G,接下来就是签名的过程,要签名的消息为 m m m
- 取 e = H A S H ( m ) e = HASH(m) e=HASH(m)
- 取 e e e的左边的 L n L_n Ln个bit长度的值为 z z z, L n L_n Ln即为前面提到的参数里 n n n的比特长度
- 从 [ 1 , n − 1 ] [1, n-1] [1,n−1]范围内,随机选择一个整数 k k k
- 利用 k k k得到椭圆曲线上的一点 ( x 1 , y 1 ) = k ⋅ G (x1,y1)=k \cdot G (x1,y1)=k⋅G
- 然后计算 r ≡ x 1 ( m o d n ) r \equiv x_1 (mod n) r≡x1(modn),如果如果 r = 0 r=0 r=0则返回步骤3重新选择 k k k
- 计算 s = k − 1 ( z + r ⋅ d A ) ( m o d n ) s = k^{-1}(z + r\cdot d_A) (mod n) s=k−1(z+r⋅dA)(modn),如果 s = 0 s=0 s=0则返回步骤3重新选择 k k k
- 得到的数字签名即为 ( r , s ) (r,s) (r,s)
验证
取点
P
=
(
X
p
,
Y
p
)
=
s
−
1
⋅
z
⋅
G
+
s
−
1
⋅
r
⋅
Q
A
P=(X_p,Y_p)= s ^ {-1} \cdot z \cdot G + s ^ {-1} \cdot r \cdot Q_A
P=(Xp,Yp)=s−1⋅z⋅G+s−1⋅r⋅QA
若
X
p
=
r
X_p=r
Xp=r,则签名有效,否则无效
Simple Proof
P
=
(
X
p
,
Y
p
)
=
s
−
1
⋅
z
⋅
G
+
s
−
1
⋅
r
⋅
Q
A
P=(X_p,Y_p)= s ^ {-1} \cdot z \cdot G + s ^ {-1} \cdot r \cdot Q_A
P=(Xp,Yp)=s−1⋅z⋅G+s−1⋅r⋅QA
因为
Q
A
=
d
A
⋅
G
Q_A=d_A \cdot G
QA=dA⋅G,故有
P
=
s
−
1
⋅
z
⋅
G
+
s
−
1
⋅
r
⋅
Q
A
P= s ^ {-1} \cdot z \cdot G + s ^ {-1} \cdot r \cdot Q_A
P=s−1⋅z⋅G+s−1⋅r⋅QA
=
s
−
1
⋅
z
⋅
G
+
s
−
1
⋅
r
⋅
d
A
⋅
G
= s ^ {-1} \cdot z \cdot G + s ^ {-1} \cdot r \cdot d_A \cdot G
=s−1⋅z⋅G+s−1⋅r⋅dA⋅G
=
s
−
1
⋅
G
⋅
(
z
+
r
⋅
d
A
)
= s ^ {-1} \cdot G \cdot {(z + r \cdot d_A)}
=s−1⋅G⋅(z+r⋅dA)
又有
s
=
k
−
1
(
z
+
r
⋅
d
A
)
(
m
o
d
n
)
s = k^{-1}(z + r\cdot d_A) (mod n)
s=k−1(z+r⋅dA)(modn)
即
s
−
1
=
k
⋅
(
z
+
r
⋅
d
A
)
−
1
(
m
o
d
n
)
s^{-1} = k\cdot(z + r\cdot d_A)^{-1} (mod n)
s−1=k⋅(z+r⋅dA)−1(modn)
代入得到
P
=
k
⋅
G
P=k \cdot G
P=k⋅G
利用冲突的随机数恢复私钥
从上面的签名过程我们可以看到最关键的地方就在于随机数k,对于一个固定的椭圆曲线,一个确定的k就意味着一个确定的r,所以如果有两个相同的私钥签署的签名出现了相同的r就代表着在生成随机数时取到了相同的k,看到这里想必你也明白了我们题目的交易签名的问题出在哪了,这两笔交易的r值相同,代表在它们签名时使用的随机数k是相同的,而这就是我们恢复私钥的关键
我们不妨设这两个签名的
z
z
z与
s
s
s分别为
z
1
z_1
z1,
z
2
z_2
z2与
s
1
s_1
s1,
s
2
s_2
s2
则有
s
1
−
s
2
=
k
−
1
(
z
1
+
d
A
⋅
r
)
−
k
−
1
(
z
2
+
d
A
⋅
r
)
s_1-s_2= k ^ {-1}(z_1 + d_A \cdot r)-k ^ {-1}(z_2+ d_A \cdot r)
s1−s2=k−1(z1+dA⋅r)−k−1(z2+dA⋅r)
=
k
−
1
(
z
1
−
z
2
)
= k ^ {-1}(z_1 - z_2)
=k−1(z1−z2)
那么
k
=
(
z
1
−
z
2
)
(
s
1
−
s
2
)
k = \frac {(z_1-z_2)}{(s_1-s_2)}
k=(s1−s2)(z1−z2)
通过
k
k
k,可以计算出
d
A
=
(
s
⋅
k
−
z
)
/
r
d_A=(s \cdot k -z) /r
dA=(s⋅k−z)/r
P2PKH
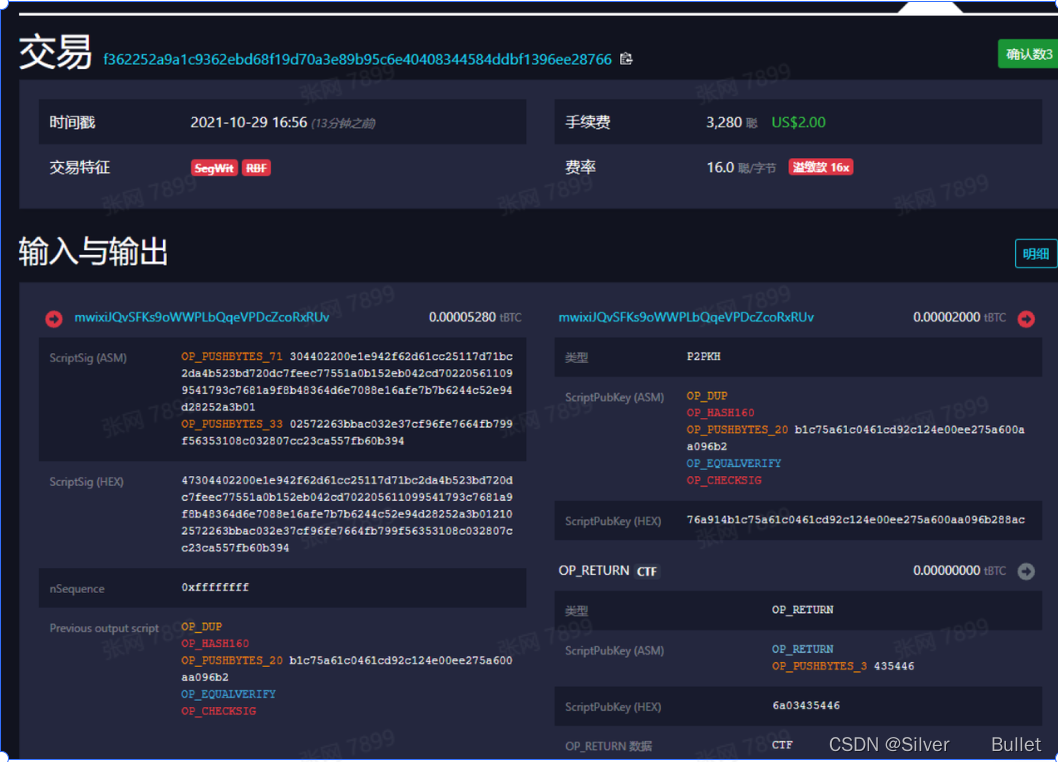
PubkeyScript是一张记录了交易记录的指令列表,它控制了下一名使用者如何解锁已接收的比特币并传送。收款人会制造一个signature script,而该文件必须满足最后一个发送者创建的PubkeyScript的参数。
PubkeyScript的参数:
- 公钥哈希(Public Key Hash) (比特币地址)
- 电子签署(ScriptSig: (r,s)+pubkey)
ASM是汇编代码
- OP_PUSHBYTES_71指压入栈中一个71字节大小的数据
- nSequence用以记录该笔交易是否可以上链
- Previous output Script用以验证当前用于支付的比特币的来源
- ScriptPubKey是一个脚本,用以验证当前用户有能力使用这个UTXO中的比特币来支付,即证明身份
OP_DUP复制栈顶数据
OP_HASH160先后进行两种hash操作然后压入栈
OP_PUSHBYTES_20将签名的hash值压入栈
OP_EQUALVERIFY比较计算签名hash和刚压入栈的hash来验证有效性,有效返回1否则返回0
OP_CHECKSIG检测栈顶的2个元素,pub key和signature是否能对应的上。对应的上,说明这个签名的私钥,和收款人的公钥可以对上。有资格花这笔钱
OP_RETURN 用来当注释,携带一些信息
Transaction hex则包含所有信息连接在一起
求解过程
提取r,s,z
脚本来源
# -*-coding:utf-8-*-
"""
@author: iceland
"""
import sys
import hashlib
import argparse
from urllib.request import urlopen
# # ==============================================================================
# parser = argparse.ArgumentParser(
# description='This tool helps to get ECDSA Signature r,s,z values from Bitcoin rawtx or txid',
# epilog='Enjoy the program! :) Tips BTC: bc1q39meky2mn5qjq704zz0nnkl0v7kj4uz6r529at')
#
# parser.add_argument("-txid", help="txid of the transaction. Automatically fetch rawtx from given txid", action="store")
# parser.add_argument("-rawtx", help="Raw Transaction on the blockchain.", action="store")
#
# if len(sys.argv) == 1:
# parser.print_help()
# sys.exit(1)
# args = parser.parse_args()
# # ==============================================================================
#
# txid = args.txid if args.txid else ''
# rawtx = args.rawtx if args.rawtx else ''
#
# if rawtx == '' and txid == '':
# print('One of the required option missing -rawtx or -txid');
# sys.exit(1)
# ==============================================================================
def get_rs(sig):
rlen = int(sig[2:4], 16)
r = sig[4:4 + rlen * 2]
# slen = int(sig[6+rlen*2:8+rlen*2], 16)
s = sig[8 + rlen * 2:]
return r, s
def split_sig_pieces(script):
sigLen = int(script[2:4], 16)
sig = script[2 + 2:2 + sigLen * 2]
r, s = get_rs(sig[4:])
pubLen = int(script[4 + sigLen * 2:4 + sigLen * 2 + 2], 16)
pub = script[4 + sigLen * 2 + 2:]
assert (len(pub) == pubLen * 2)
return r, s, pub
# Returns list of this list [first, sig, pub, rest] for each input
def parseTx(txn):
if len(txn) < 130:
print('[WARNING] rawtx most likely incorrect. Please check..')
sys.exit(1)
inp_list = []
ver = txn[:8]
if txn[8:12] == '0001':
print('UnSupported Tx Input. Presence of Witness Data')
sys.exit(1)
inp_nu = int(txn[8:10], 16)
first = txn[0:10]
cur = 10
for m in range(inp_nu):
prv_out = txn[cur:cur + 64]
var0 = txn[cur + 64:cur + 64 + 8]
cur = cur + 64 + 8
scriptLen = int(txn[cur:cur + 2], 16)
script = txn[cur:2 + cur + 2 * scriptLen] # 8b included
r, s, pub = split_sig_pieces(script)
seq = txn[2 + cur + 2 * scriptLen:10 + cur + 2 * scriptLen]
inp_list.append([prv_out, var0, r, s, pub, seq])
cur = 10 + cur + 2 * scriptLen
rest = txn[cur:]
return [first, inp_list, rest]
# ==============================================================================
def get_rawtx_from_blockchain(txid):
try:
htmlfile = urlopen("https://blockchain.info/rawtx/%s?format=hex" % txid, timeout=20)
except:
print('Unable to connect internet to fetch RawTx. Exiting..')
sys.exit(1)
else:
res = htmlfile.read().decode('utf-8')
return res
# =============================================================================
def getSignableTxn(parsed):
res = []
first, inp_list, rest = parsed
tot = len(inp_list)
for one in range(tot):
e = first
for i in range(tot):
e += inp_list[i][0] # prev_txid
e += inp_list[i][1] # var0
if one == i:
e += '1976a914' + HASH160(inp_list[one][4]) + '88ac'
else:
e += '00'
e += inp_list[i][5] # seq
e += rest + "01000000"
z = hashlib.sha256(hashlib.sha256(bytes.fromhex(e)).digest()).hexdigest()
res.append([inp_list[one][2], inp_list[one][3], z, inp_list[one][4], e])
return res
# ==============================================================================
def HASH160(pubk_hex):
return hashlib.new('ripemd160', hashlib.sha256(bytes.fromhex(pubk_hex)).digest()).hexdigest()
# ==============================================================================
txn = '010000000153db4e56f159c0679818ef8ce814ce8fcaad12b854da7e582fb5f19266945f63000000006a47304402200e1e942f62d61cc25117d71bc2da4b523bd720dc7feec77551a0b152eb042cd7022030d7d78612b765dff96dd14fc5d723e06a8fa61b42a93410236273baf82f7f15012102572263bbac032e37cf96fe7664fb799f56353108c032807cc23ca557fb60b394ffffffff02d0070000000000001976a914b1c75a61c0461cd92c124e00ee275a600aa096b288ac0000000000000000056a0343544600000000'
# if rawtx == '':
# rawtx = get_rawtx_from_blockchain(txid)
print('\nStarting Program...')
m = parseTx(txn)
e = getSignableTxn(m)
for i in range(len(e)):
print('=' * 70,
f'\n[Input Index #: {i}]\n R: {e[i][0]}\n S: {e[i][1]}\n Z: {e[i][2]}\nPubKey: {e[i][3]}')
求dA
#-*-coding:utf-8-*-
r1 = 0x0e1e942f62d61cc25117d71bc2da4b523bd720dc7feec77551a0b152eb042cd7
s1 = 0x5611099541793c7681a9f8b48364d6e7088e16afe7b7b6244c52e94d28252a3b
z1 = 0x5ecd4154a2db20480d7715d6e47a772aaf596e11e6f16a4d58e9f0d260294660
r2 = 0x0e1e942f62d61cc25117d71bc2da4b523bd720dc7feec77551a0b152eb042cd7
s2 = 0x30d7d78612b765dff96dd14fc5d723e06a8fa61b42a93410236273baf82f7f15
z2 = 0x50f1c6205aab5f8dac7b505f91dfc437b1b13cd00f12a492570a040a27c38e25
assert r1 == r2
r = r1
def inverse_mod( a, m ):
"""Inverse of a mod m."""
if a < 0 or m <= a: a = a % m
c, d = a, m
uc, vc, ud, vd = 1, 0, 0, 1
while c != 0:
q, c, d = divmod( d, c ) + ( c, )
uc, vc, ud, vd = ud - q*uc, vd - q*vc, uc, vc
assert d == 1
if ud > 0: return ud
else: return ud + m
def derivate_privkey(p, r, s1, s2, z1, z2):
z = z1 - z2
s = s1 - s2
r_inv = inverse_mod(r, p)
s_inv = inverse_mod(s, p)
k = (z * s_inv) % p
d = (r_inv * (s1 * k - z1)) % p
return d, k
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
privatekey,k=derivate_privkey(p,r,s1,s2,z1,z2)
利用私钥解密AES
import base64
cipher = base64.b64decode(b"4w/VLHqPZi/epoOGvjoY9TZWhDtYpL3iLsUTyvzghJM=")
privatekey = 0xF41AA419CB6BD43F322D403F40728CE9784CD0B465F409322A76A3DF0A984A29
from Crypto.Cipher import AES
from Crypto.Util.number import *
key = long_to_bytes(privatekey)[0:16]
iv = long_to_bytes(privatekey)[16:]
aes = AES.new(key=key,iv=iv,mode=AES.MODE_CBC)
flag = aes.decrypt(cipher.encode())
print(flag)
参考链接

![[Vue warn]: You may have an infinite update loop in a component render function](https://img-blog.csdnimg.cn/91384222b9db42bfa926cd45e947ceed.png)