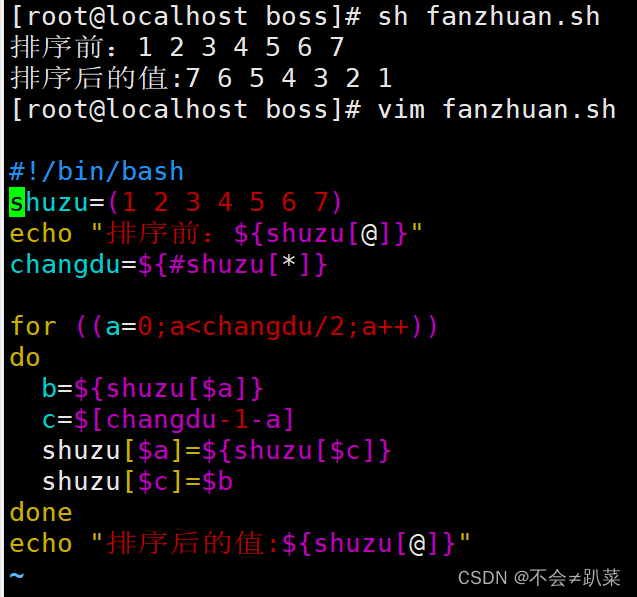
码距

一个编码系统的码距是任意两个码字的最小距离。

例如个编码系统采用三位长度的二进制编码，若该系统有四种编码分别为：000，011，100，111，此编码系统中000与111的码距为3；011与000的码距为2；011与111的码距为1，则该编码系统的码距为1。

码距计算方法：两个编码按位异或后1的个数。101异或100 = 001，1的个数为1，所以码距为1。

为了检测e个误码，最小码距d满足：d>=e+1；为了纠正t个误码，最小码距d满足：d>=2t+1

循环校验码

数据发送、接受方约定一个“除数”，在K个信息位后拼接R个校验位作为“被除数”，添加校验位后需保证除法的余数为0。收到数据后，进行除法检查余数是否为0，若余数非0说明出错，则进行重传或纠错。

例如：原始报文为"1100101"，其生成多项式为"x⁴+x³+x+1"，求CRC编码结果？

1. K=原始报文长度=7，R=生成多项式最高次幂=4，“除数”为生成多项式对应二进制码11011
2. 原始报文左移R位，低位补0，求得“被除数”（11001010000）
3. 做模2除法产生余数：1001
   
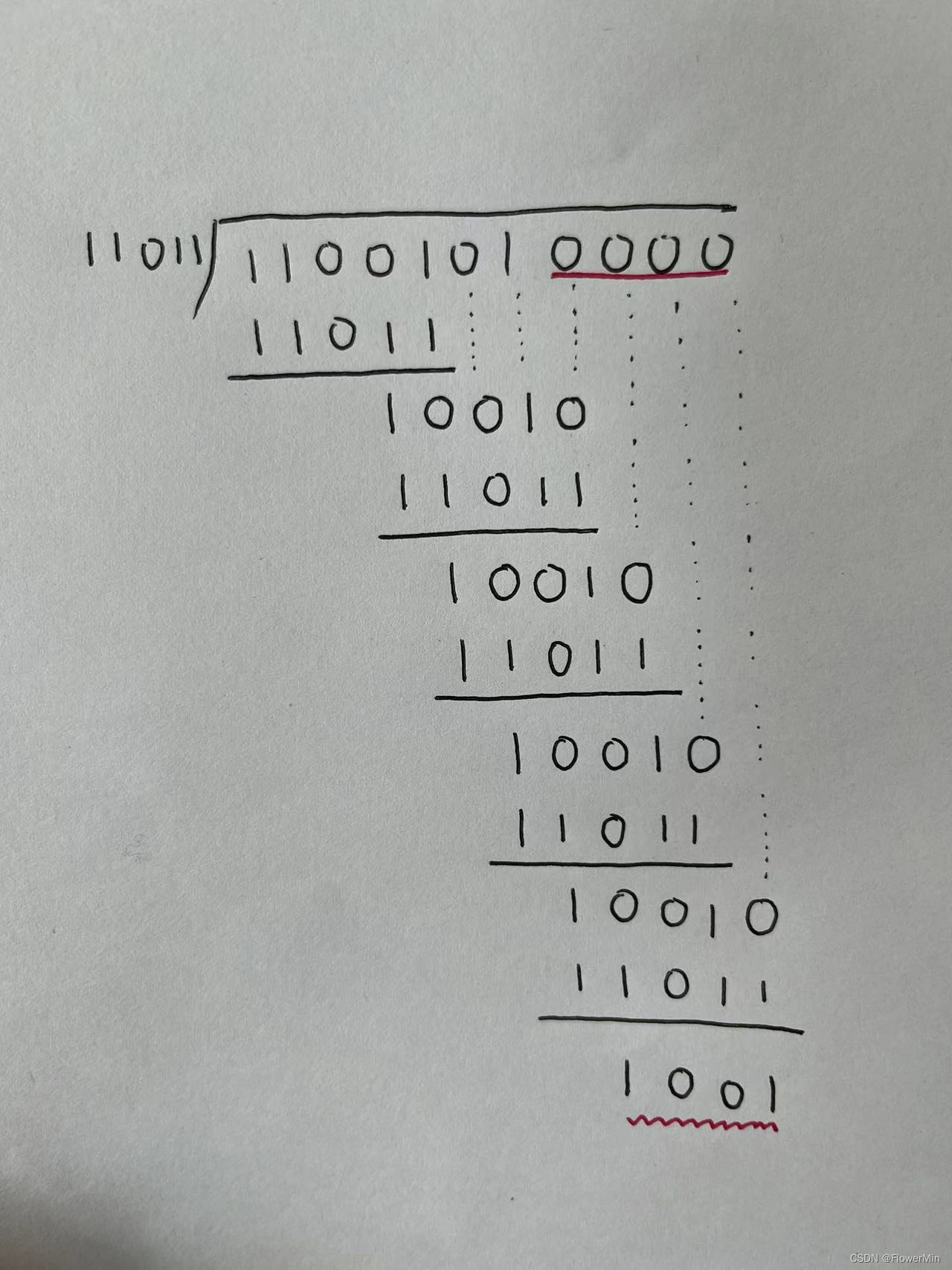
4. 求得CRC编码为：11001011001

海明校验码

海明校验码是一种多重奇偶检错系统，求海明码时的一项基本考虑是确定所需最少的校验位数k。考虑长度为m位的信息，若附加了k 个校验位，则所发送的总长度为m+k。在接收器中要进行k个奇偶检查，每个检查结果或是真或是伪，k位的校验码可以用来确定误码的位置。m与k的关系：2^k≥m+k+1

求信息1011的海明码？

1. 根据公式2^k≥4+k+1，有k=3，3位校验码从低到高需要放在2⁰=1，2¹=2，2²=4三个位置上，则信息位需要放在第3，5，6，7四个位置，记为M1，M2，M3，M4，如下表。

7	6	5	4	3	2	1	位数
M4=1	M3=0	M2=1		M1=1			信息位
			k3		k2	k1	校验位
k1+k2+k3	k2+k3	k1+k3		k1+k3			校验位组

2. 计算校验位组。7=2⁰+2¹+2²=1+2+4，表示第7位置的M4需要用1位置的k1、2位置的k2和4位置的k3进行校验，同理计算k1、k2、k3也与M4有关。依次计算M1到M4对应的校验位组，如上表。
3. 求校验位的值，如下图所示：
   
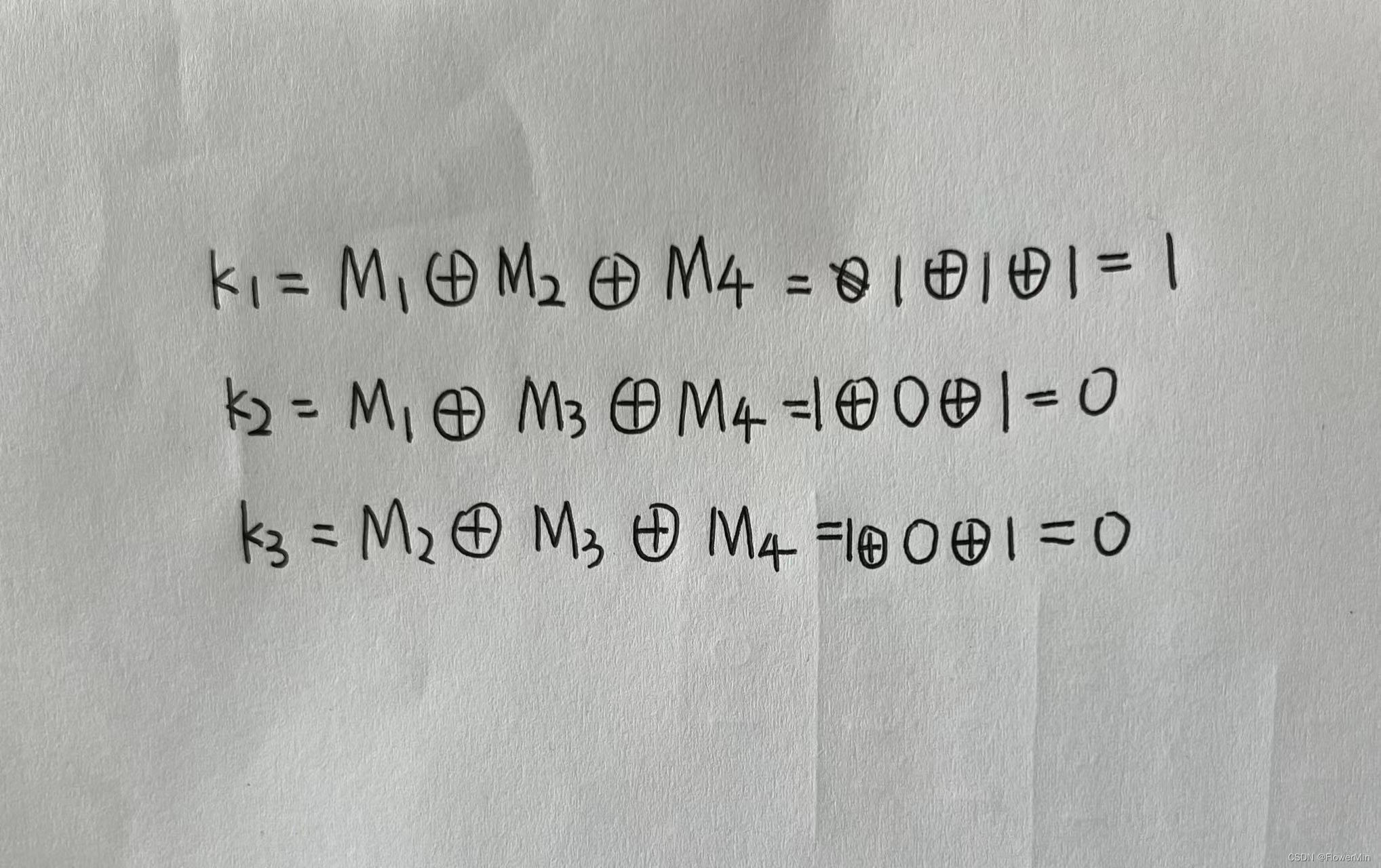
4. 将1-7位拼接为海明码：1010101

在接收方，也可以根据校验位对接收到的信息进行测试，例如收到1011101，如何校验？

5. 根据前述流程提取出‘1011101’的信息位1011，校验位101
6. 由信息位1011按步骤计算出校验位001
7. 101异或001得出结果100（只有得出结果000说明传输无误）二进制100表示第4位置出错