已完成全部可以领取,详情看文末!!!
数维杯A题思路
A题是这次比赛比较难的题目,地下水系统水体污染问题,他给出了我们一些行为特征,污染物的行为特征主要涉及对流迁移、水动力弥散、吸附及阻滞等物理过程、化学反应过程以及生物转化过程等。
问题1 通过查阅相关文献和资料,分析并建立河流-地下水系统中有机污染物的对流、弥散及吸附作用的数学模型。
要解决这个问题,我们首先要理解有机污染物在地下水中迁移的基本物理过程。这个过程包括对流、弥散和吸附三个主要部分。对流是指有机污染物随着地下水流动而移动,弥散是指有机污染物在水流中扩散,而吸附则是有机污染物被河流沉积物吸附。
这些过程可以通过对流-弥散-吸附模型来描述,该模型是一个偏微分方程,形式如下:
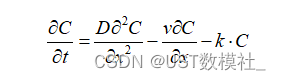
其中,C是有机污染物的浓度,t是时间,x是空间位置,D是弥散系数,v是平均孔隙流速,k是吸附系数。
在建立模型时,我们首先要假设地下水渗流场是各向同性的,这意味着各个方向的性质都是相同的,这样可以简化问题的复杂性。然后我们要考虑到有机污染物的对流、弥散和吸附过程,将这些过程以数学的形式表达出来,得到上述的偏微分方程。
在模型中,对流项v∂C/∂x表示有机污染物随地下水流动的速度,弥散项D∂²C/∂x²表示有机污染物在水流中的扩散,而吸附项-k·C则表示有机污染物被河流沉积物吸附的速度。
问题2 试利用下面介绍的内容和表中试验参数以及数据依据数学模型研究某有机污染物在河流-地下水系统中的迁移转化机理。
解决这个问题需要利用给出的实验数据,通过数值计算方法解决上述的偏微分方程,以了解有机污染物在地下水中的迁移规律。
首先,我们需要确定模型中的参数D,v,k。这些参数可以通过对流和弥散试验参数以及吸附动力学试验结果来确定。具体来说,平均孔隙流速u可以直接作为对流速度v,弥散系数D可以直接从试验数据中获取,而吸附系数k则可以通过吸附动力学试验结果来确定。这样,我们就得到了模型的所有参数。
在解决方程时,我们需要设置一定的初始条件和边界条件,以模拟实际的地下水流动情况。初始条件一般为污染物的初始浓度,而边界条件则需要考虑到地下水流动的方向和速度。
在获得了数值解后,我们可以分析污染物浓度随时间和空间的变化情况,以了解有机污染物在地下水中的迁移规律。此外,我们还可以通过比较模型的预测结果和实际的试验数据,来验证模型的准确性。
问题3 生物降解是污染物一个很重要的转化过程,考虑生物降解作用对有
机污染物转化的影响,建立适当的数学模型,试结合表4中的试验数据分析微生物对该有机污染物的降解特性。
在考虑生物降解影响时,我们需要将生物降解过程添加到原来的模型中。生物降解过程可以看作是一个消耗有机污染物的过程,可以用一个新的项来表示。因此,新的模型可以写成:

其中,B是生物降解系数,表示微生物降解有机污染物的速度。
在确定了新的模型后,我们同样需要通过数值计算方法来解决这个偏微分方程。这时,我们需要使用表4中的试验数据来确定生物降解系数B,然后再使用同样的方法解决新的偏微分方程。
在解决了新的偏微分方程后,我们可以分析有机污染物浓度随时间和空间的变化情况,以了解生物降解对有机污染物迁移的影响。此外,我们还可以通过比较模型的预测结果和实际的试验数据,来验证模型的准确性。
数维杯B题思路
B题是一个优化类问题,涉及到城市轨道交通系统的能源优化问题,特别是列车的动态驾驶策略,还是需要一定的专业性。
问题一:你如何通过建模方法编写程序以获得列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线?程序的运行时间是多长?需要获取列车以最短时间到达站台B、在最短运行时间上分别增加10s、20s、50s、150s、300s到达站台B总共六组曲线。
在这个问题中,我们需要构建一个物理模型来描述列车的运行情况。首先,我们可以使用牛顿第二定律来描述列车的动力学行为。在任何给定的时间点,列车的加速度(或减速度)由以下力量决定:列车电机的牵引力,空气阻力,轨道阻力,以及由于列车旋转部件惯性的影响。
我们可以将这些力量表示为以下的微分方程:
![]()
然后,我们可以使用数值方法(例如欧拉法或龙格-库塔法)来求解这个微分方程,并得到列车运行过程中的速度、位置、牵引制动力和能量消耗的变化情况。
问题二:考虑附件一、二的路况信息以及电机的复杂动态过程。若列车计划运行时间为 T,请你设计优化方案得到可行的速度轨迹,使得运行过程的能耗降低(越低越好)。参照问题一,获取列车以最短时间到达站台 B、在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线。列车在运行过程中可能会出现各种突发情况导致列车需要提前到达站台或延时到达站台。列车的运行速度轨迹需要根据新的到站时间而发生变化。
在这个问题中,我们需要考虑更复杂的情况,包括不同路段的限速、不同的坡度情况,以及电机的动态特性。对于这些复杂情况,我们可以在问题1的基础上进一步完善模型。
对于不同路段的限速,我们可以在模型中引入限速函数,该函数会在列车运行到对应路段时调整列车的最大速度。
对于不同的坡度情况,我们可以在计算阻力时考虑列车的势能变化,即引入重力势能项。
对于电机的动态特性,我们可以根据附件二的数据调整电机的牵引力和制动力的计算方法。
在这个问题中,我们还需要进行能耗优化。这通常需要使用最优化方法,如动态规划或者遗传算法等。我们可以定义一个能耗函数,然后通过调整列车的驾驶策略(例如,加速、减速、巡航的时间等)来最小化总能耗。在这个过程中,我们需要考虑列车的运行时间,以确保列车能在规定的时间内到达目的地。
问题 3:列车从起点出发,原计划于 320s 后到达终点,列车运行至 2000m 位置时,由于前方突发事故,需要延迟 60s 到达终点。请你设计优化方案在保持列车节能运行下,能够快速地(越快越好)得到调整后的优化速度轨迹。作出列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线。
这个问题是一个典型的在线优化问题,也就是在列车运行过程中,需要根据实时的情况调整驾驶策略。这种情况下,我们需要使用在线算法或者预测控制的方法来解决。
当列车运行至2000m位置时,我们可以获取到列车的当前状态(例如,速度、位置等),以及需要延迟60s到达终点的新要求。然后,我们可以使用预测控制的方法来调整剩余路程的驾驶策略。具体来说,我们可以在每个时间点,预测未来的状态,并在预测的基础上选择最优的控制输入(例如,是否加速、减速或者巡航,以及加速或减速的幅度等)。
这个问题的关键在于如何设计预测模型和优化算法。对于预测模型,我们可以基于问题1和问题2的物理模型,考虑列车的动力学行为、路况信息和电机的动态特性等因素。对于优化算法,我们需要选择一个能够快速求解的算法,例如,梯度下降法、模拟退火算法或者遗传算法等。
数维杯C题思路
C题相对来说要简单一点,是一个大数据类的题目,考察我们对数据的处理分析能力。
问题一:根据附件1与附件2,分析两个医院的临床数据有无显著性差异,若存在显著性差异,对导致这种差异的因素进行分析。
为了确定两个医院的临床数据是否有显著性差异,我们可以使用统计学中的假设检验方法。这类方法基于数据生成了一个统计量,并计算这个统计量在原假设下的概率,也就是p值。如果p值非常小(例如,小于0.05或者0.01),那么我们就有足够的证据拒绝原假设,认为两个医院的数据存在显著性差异。
常用的假设检验方法有t检验(用于两个样本的均值比较)、卡方检验(用于类别变量的比较)和方差分析(用于三个或者更多样本的均值比较)等。我们需要根据具体的数据特性来选择合适的方法。例如,如果附件1中的身体指标和节育器的理化指标都是连续变量,那么我们可能需要使用t检验或者方差分析。如果附件2中的主诉情况是类别变量,那么我们可能需要使用卡方检验。
如果发现两个医院的数据存在显著性差异,那么我们需要进一步分析导致这种差异的可能因素。这可能包括医院的操作技术、病人的体质差异、环境因素等。我们可以通过收集更多的数据或者进行深入的访谈来探索这些因素。
问题二:结合附件1与附件2,分析受试者的身体指标与随访主诉情况的联系,并说明受试者的身体指标是否是受试者出现不适状况的主要因素。
要分析受试者的身体指标与随访主诉情况的联系,我们可以使用统计学中的回归分析方法。回归分析是一种统计方法,用于研究变量之间的关系。在这个问题中,我们可以把随访主诉情况看作因变量,身体指标看作自变量,建立一个回归模型,预测因变量对自变量的反应。
如果附件2中的主诉情况是二分类变量(例如,有不适症状和无不适症状),那么我们可以使用逻辑回归模型。如果主诉情况是多分类变量,那么我们可以使用多项式逻辑回归模型。我们还需要考虑可能存在的混淆变量,例如年龄、性别等,这些变量可能同时影响身体指标和主诉情况。
通过分析回归模型的参数估计,我们可以判断身体指标是否是受试者出现不适状况的主要因素。例如,如果某个身体指标的系数显著不为零,那么我们可以认为这个指标是出现不适状的主要因素。如果所有身体指标的系数都不显著,那么我们可以认为身体指标可能不是主要因素。我们也可以通过计算模型的拟合优度,例如决定系数R^2,来评估身体指标对主诉情况的解释力度。
问题三:根据受试者的身体指标、节育器的理化指标与随访时的主诉情况,建立节育器质量模型,并分析VCu260与VCu380 记忆型宫内节育器的质量哪个更优,更适合生产。
对于建立节育器质量的模型,我们需要综合考虑受试者的身体指标、节育器的理化指标以及随访时的主诉情况。一种可能的方法是使用多元线性回归或者多元逻辑回归模型,其中因变量是节育器质量,自变量是身体指标和理化指标,以及随访时的主诉情况。
我们可以使用一些衡量节育器质量的指标,例如避孕成功率、使用者的舒适度、使用者的满意度等。我们需要将这些指标量化,然后使用回归模型进行分析。通过比较VCu260和VCu380记忆型宫内节育器的模型参数,我们可以判断哪种节育器的质量更优,更适合生产。
问题四:结合问题3,根据建立的节育器质量模型,探究影响宫内节育器质量的决定因素。
根据上述的节育器质量模型,我们可以探究影响节育器质量的决定因素。在模型中,每个自变量的系数都代表了这个变量对于节育器质量的影响力度。如果系数显著不为零,那么我们可以认为这个变量是一个决定因素。
我们可以分别考察身体指标和理化指标对节育器质量的影响。比如,如果某个身体指标的系数很大,那么我们可以认为这个身体指标对节育器质量的影响很大。如果某个理化指标的系数很大,那么我们可以认为这个理化指标对节育器质量的影响很大。
我们还可以通过模型的交互项来探究身体指标和理化指标之间的交互影响。例如,如果某两个指标的交互项系数显著不为零,那么我们可以认为这两个指标之间存在显著的交互作用,这可能影响节育器的质量。