【HDU No. 4902】 数据结构难题 Nice boat

杭电OJ 题目地址

【题意】

有n 个数字a 1 , a 2 , …, an ，每次都可以将[l , r ]区间的每个数字都更改为数字x （类型1），或将[l ,r ]区间每个大于x 的ai 都更改为最大公约数gcd(ai , x )（类型2），请输出最后的序列。

【输入输出】

输入：

第1行包含一个整数T ，表示测试用例的数量。每个测试用例的第1行都包含整数n 。下一行包含以空格分隔的n 个整数a 1 , a 2 ,…, an 。再下一行包含一个整数Q ，表示操作数量。下面的Q 行，每行都包含4个整数t 、l 、r 、x ，t 表示操作类型，l 、r 表示区间左右端点。T ≤2，n , Q ≤100000，ai , x ≥0且在int32范围内。

输出：

对每个测试用例，都单行输出以空格分隔的最终序列，在序列结束后输出一个空格。

【样例】

【思路分析】

本题是很明显的区间更新问题，但不仅仅是简单的区间更新，而是将[l , r ]区间每个大于x 的ai 都更改为gcd(ai , x )。

【算法设计】

① 创建线段树。

② 区间更新（类型1），将[l , r ]区间的每个数字都更改为数字x。

③ 区间更新（类型2），将[l , r ]区间每个大于x 的ai 都更改为gcd(ai , x )。

【举个栗子】

① 创建线段树。根据输入样例，首先输入10个数，将其存储在数组中。

由于数值较大，为了方便起见，在下图中标记的是数值对应的下标，在程序中记录的是数值自身data[i ]。初时化时，区间最大值、懒标记等于数据自身，maxs[i ]=lazy[i ]=data[i ]。

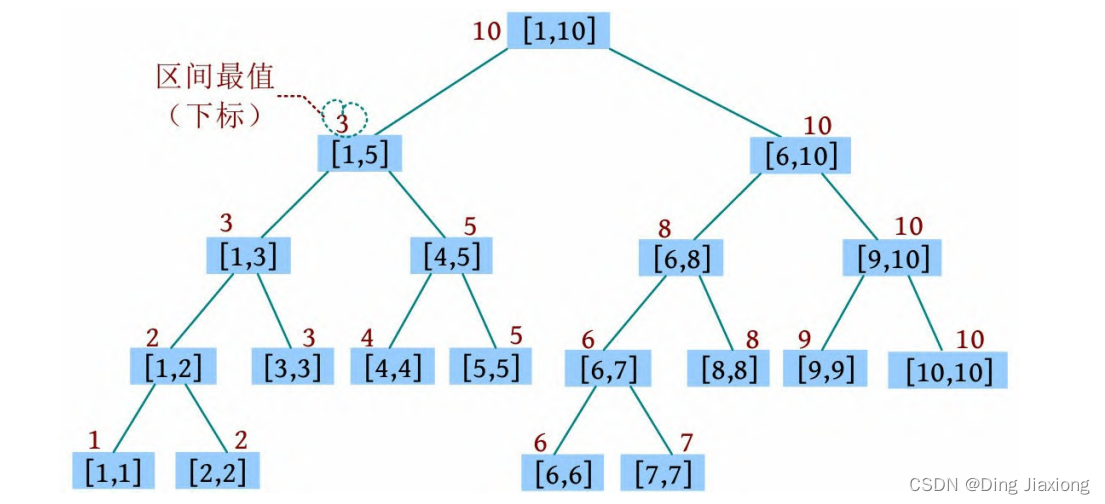
② 1 3 6 74243042：将[3, 6]区间的值修改为x （x=74243042，用下标11标识）。找到[3, 3]、[4, 5]、[6, 6]区间，更新这些区间的懒标记和最大值为x ，返回时更新最大值。

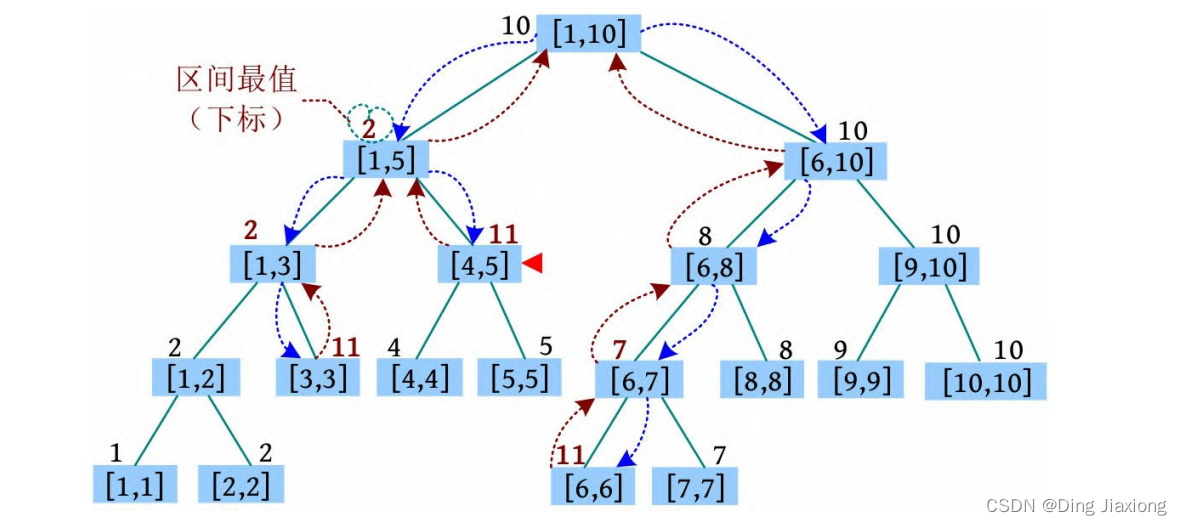
③ 2 4 8 16531729：将[4, 8]区间大于x （x =16531729）的值修改为两者的最大公约数。首先找到[4, 5]、[6, 8]区间。[4, 5]区间带有懒标记，因此更新该区间的懒标记和最大值：lazy[i]=gcd(lazy[i ], x )=1，maxs[i ]=lazy[i ]=1。返回时更新最大值。[6, 8]区间没有懒标记，说明该区间的数值不同，因此继续查找左右子树，更新[6, 6]、[7, 7]、[8, 8]区间。该区间的懒标记lazy[i]=gcd(lazy[i ], x )=1，最大值maxs[i ]=lazy[i ]=1。返回时更新最大值。

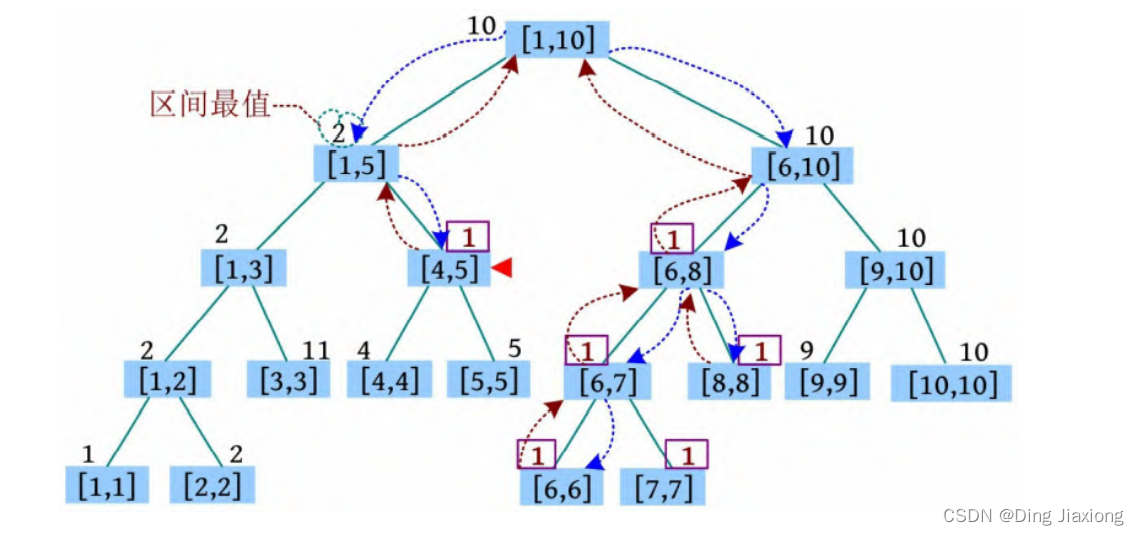
④ 1 3 4 1474833169：将[3, 4]区间的值修改为x （x=1474833169，用下标12标识）。找到[3, 3]、[4, 4]区间，更新这些区间的懒标记和最大值为x ，返回时更新最大值。在查找区间的过程中因为[4, 5]区间带有懒标记，所以懒标记下传，再更新[4, 4]区间。

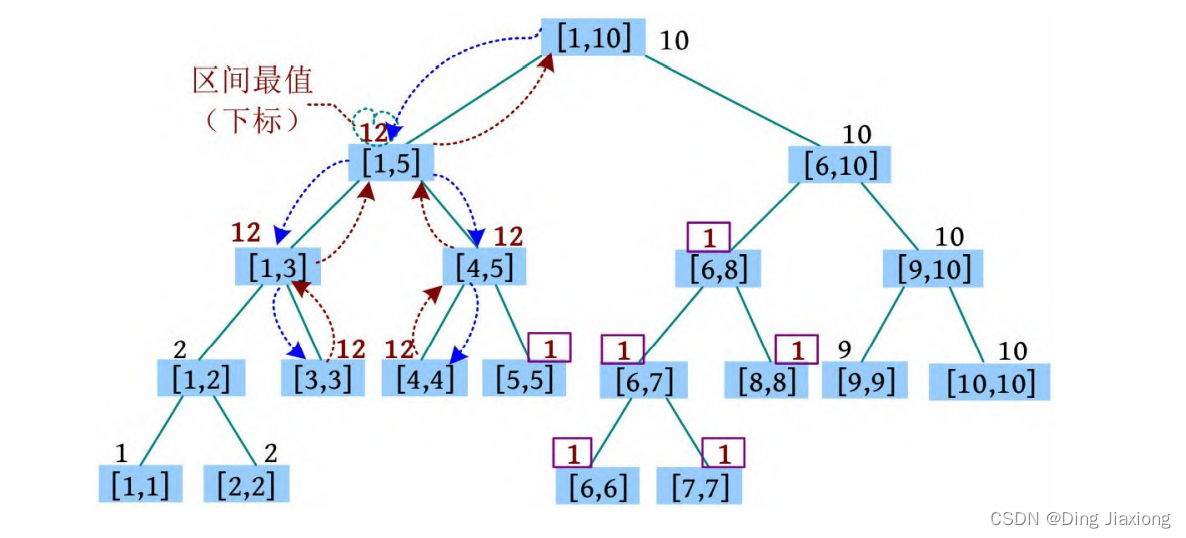
⑤ 2 1 8 1131570933：将[1, 8]区间大于x （x =1131570933）的值修改为两者的最大公约数。首先找到[1, 5]、[6, 8]区间。[6, 8]区间的最大值比x 小，什么也不做。[1, 5]区间没有懒标记，说明该区间内的数值不同，因此继续查找左右子树，更新[1, 2]、[3, 3]、[4,4]、[5, 5]区间，其中[1, 2]、[5, 5]区间的最大值比x 小，什么也不做。只需更新[3, 3]、[4, 4]区间的懒标记和最大值：lazy[i]=gcd(lazy[i ], x )=1，maxs[i ]=lazy[i ]=1，返回时更新最大值。

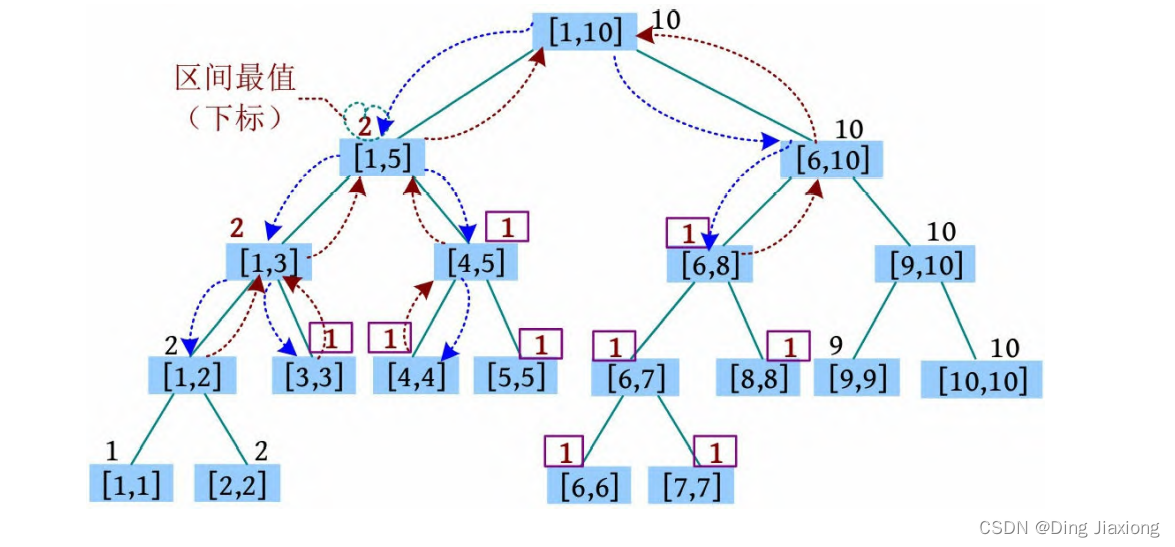
⑥ 2 7 9 1505795335：将[7, 9]区间大于x （x =1505795335）的值修改为两者的最大公约数。首先找到[7, 7]、[8, 8]、[9, 9]区间，这3个区间的最大值比x 小，什么也不做。

⑦ 2 3 7 101929267：将[3, 7]区间大于x （x =101929267）的值修改为两者的最大公约数。首先找到[3, 3]、[4, 5]、[6, 7]区间，这3个区间的最大值比x 小，什么也不做。

⑧ 1 4 10 1624379149：将[4, 10]区间的值修改为x （x=1624379149，用下标13标识）。找到[4, 5]、[6, 10]区间，更新这些区间的懒标记和最大值为x ，返回时更新最大值。

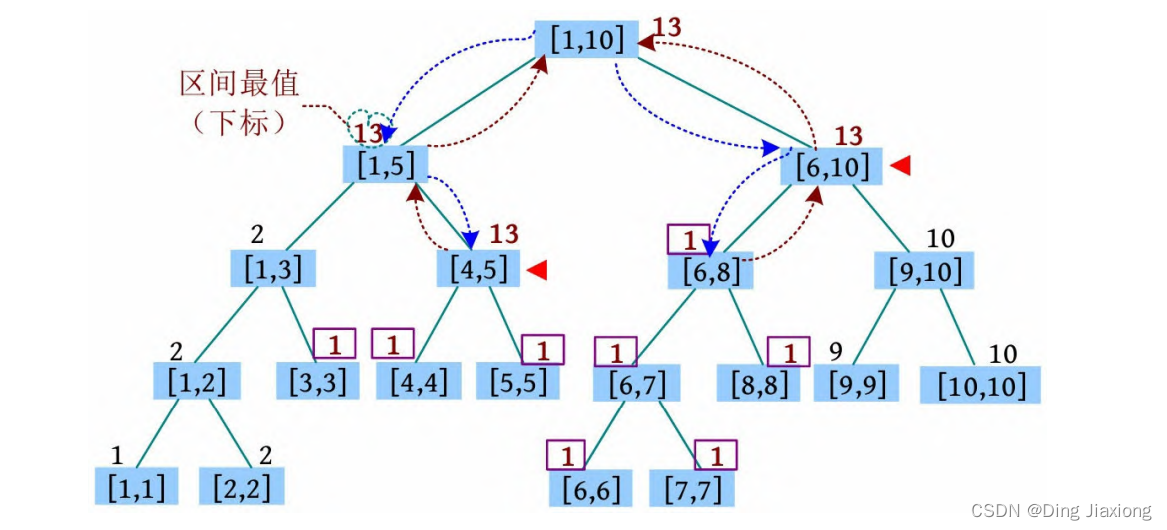
⑨ 2 2 8 2110010672：将[2, 8]区间大于x （x =2110010672）的值修改为两者的最大公约数。首先找到[1, 10]区间，该区间的最大值比x 小，什么也不做。

⑩ 2 6 7 156091745：将[6, 7]区间大于x （x =156091745）的值修改为两者的最大公约数。首先找到[6, 7]区间，在查找过程中经过的[6, 10]区间带有懒标记，懒标记下传，一直找到[6, 7]区间，该区间带有懒标记，因此更新该区间的懒标记和最大值：lazy[i]=gcd(lazy[i ], x )=1，maxs[i ]=lazy[i ]=1，返回时更新最大值。

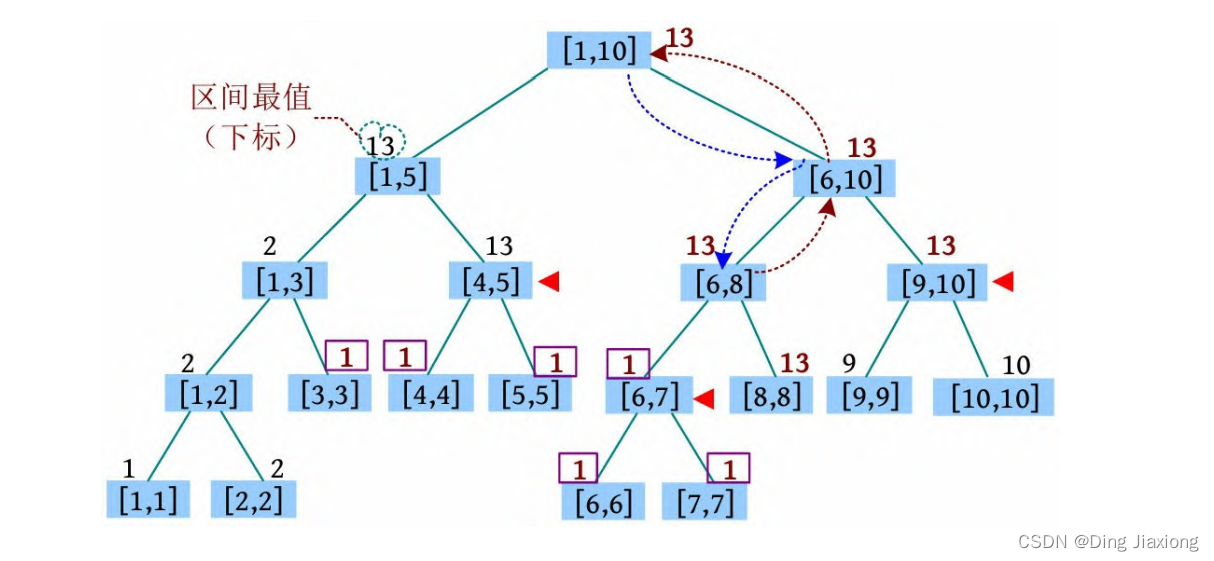
⑪ 1 2 5 937186357：将[2, 5]区间的值修改为x （x=937186357，用下标14标识）。找到[2, 2]、[3, 3]、[4, 5]区间，更新这些区间的懒标记和最大值为x ，返回时更新最大值。

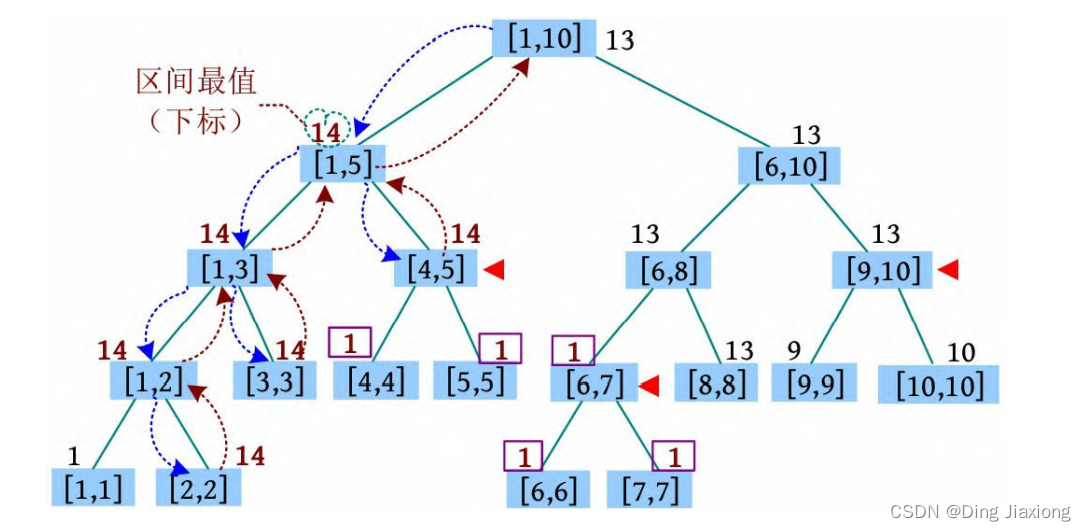
⑫ 输出结果。因为节点可能带有懒标记，因此在查找叶子的过程中懒标记下传，然后输出叶子即可。上图中[4, 5]、[6, 7]、[9,10]区间带有懒标记，懒标记下传后如下图所示。

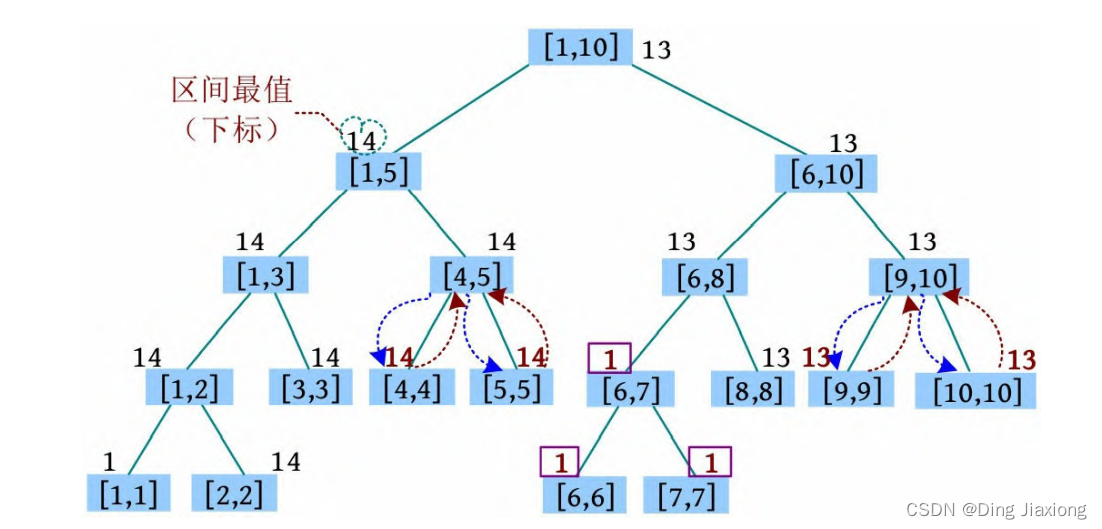
所有叶子节点的数据为1、937186357、937186357、937186357、937186357、1、1、1624379149、1624379149、1624379149。

【算法实现】

① 区间更新（类型1）。将[l , r ]区间的每个数字都更改为数字x ，找到区间后更新最大值为x 。在查找过程中下传懒标记，返回时更新最大值。

void update1(int x,int L,int R,int l,int r,int i) // 将[L,R] 区间的每个数字都更改为数字 x
{
    if(L<=l&&r<=R) // 区间覆盖
    {
        lazy[i]=maxs[i]=x; // 懒标记，最大值
        return ;
    }
    PushDown(i); // 下传懒标记
    int mid=(l+r)>>1; 
    if(L<=mid)
    	update1(x,L,R,ls); // #define ls l , mid ,i << 1
    if(R>mid)
    	update1(x,L,R,rs); // #define rs mid + 1 , r , i << 1 | 1
    PushUp(i); // 上传、更新最大值
}

② 区间更新（类型2）。将[l , r ]区间每个大于x 的ai 都更改为gcd(ai , x )。若该区间的最大值小于或等于x ，则什么也不做，因此在操作过程中可记录区间最大值，提高效率。若懒标记不为0，且待更新区间覆盖当前节点区间，则lazy[i ]=gcd(lazy[i ], x )，maxs[i ]=lazy[i ]，返回。懒标记下传，更新左右子树，返回时更新最大值。

void update2(int x,int L,int R,int l,int r,int i)
{
    if(maxs[i]<=x) return ;
    if(lazy[i]&&L<=l&&r<=R)
    {
        lazy[i]=gcd(lazy[i],x); // gcd() 为求最大公约数
        maxs[i]=lazy[i];
        return ;
    }
    PushDown(i); // 懒标记下传
    int mid=(l+r)>>1; 
    if(L<=mid)
    	update2(x,L,R,ls);
    if(R>mid)
    	update2(x,L,R,rs);
    PushUp(i); // 上传、更新最大值
}

[完整AC代码]

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

#define N 100005
#define lson i<<1
#define rson i<<1|1
#define ls l,mid,i<<1
#define rs mid+1,r,i<<1|1

int maxs[N<<2],lazy[N<<2];
int n,m;

int gcd(int a,int b)//最大公约数 
{
    if(!b) return a;
    else return gcd(b,a%b);
}
void PushUp(int i)//上传 
{
    maxs[i]=max(maxs[lson],maxs[rson]);
}
void PushDown(int i)//下传 
{
    if(lazy[i])
    {
        lazy[lson]=lazy[rson]=lazy[i];
        maxs[lson]=maxs[rson]=maxs[i];
        lazy[i]=0;
    }
}
void build(int l,int r,int i)
{
    if(l==r)
    {
    	scanf("%d",&lazy[i]);
    	maxs[i]=lazy[i];
    	return ;
	}
    int mid=(l+r)>>1;
    build(ls);
    build(rs);
    PushUp(i);
}
 
void update1(int x,int L,int R,int l,int r,int i)
{
    if(L<=l&&r<=R)
    {
        lazy[i]=maxs[i]=x;
        return ;
    }
    PushDown(i);
    int mid=(l+r)>>1;
    if(L<=mid)
    	update1(x,L,R,ls);
    if(R>mid)
    	update1(x,L,R,rs);
    PushUp(i);
}
 
void update2(int x,int L,int R,int l,int r,int i)
{
    if(maxs[i]<=x) return ;
    if(lazy[i]&&L<=l&&r<=R)
    {
        lazy[i]=gcd(lazy[i],x);
        maxs[i]=lazy[i];
        return ;
    }
    PushDown(i);
    int mid=(l+r)>>1;
    if(L<=mid)
    	update2(x,L,R,ls);
    if(R>mid)
    	update2(x,L,R,rs);
    PushUp(i);
}
 
void print(int l,int r,int i)
{
    if(l==r)
    {
    	printf("%d ",lazy[i]);
    	return ;
	}
	PushDown(i);
    int mid=(l+r)>>1;
    print(ls);
    print(rs);
}

void print2(int l,int r,int i)//测试 
{
	if(maxs[i])
	{
		printf("%d %d\n",lazy[i],maxs[i]);
	    int mid=(l+r)>>1;
	    print2(ls);
	    print2(rs);
	}
}

int main()
{
	
    int T,l,r,opt;
    int x;
    scanf("%d",&T);
	
    while(T--)
    {
        scanf("%d",&n);
        build(1,n,1);
        //print2(1,n,1);
        scanf("%d",&m);
        while(m--)
        {
            scanf("%d%d%d%d",&opt,&l,&r,&x);
            if(opt==1) update1(x,l,r,1,n,1);
            else update2(x,l,r,1,n,1);
            //print2(1,n,1);
        }
        print(1,n,1);
        printf("\n");
    }
	
    return 0;
}