集合的表示

集合运算概述

交、并、补、差，判定一个元素是否属于某一个集合

并查集

集合并、查某元素属于什么集合

我们最主要关心的就是集合的两个运算，一个是把两个集合并起来；另一个是查找某一个元素是属于哪个集合的。

【例】有10台电脑{1,2,3，...，9,10}，已知下列电脑之间已经实现了连接：

1和2、2和4、3和5、4和7、5和8、6和9、6和10

问：2和7之间，5和9之间是否是连通的？

解决思路

（1）将10台电脑看成10个集合{1}，{2}，{3}，...，{9}，{10}；

（2）已知一种连接“x和y”，就将x和y对应的集合合并；

（3）查询“x和y是否是连通的”就是判别x和y是否属于同一集合。

已经清楚思路了，那么在这样的并查集问题中集合存储要如何实现呢？

可以用树结构表示集合，树的每个结点代表一个集合元素

树结构表示集合

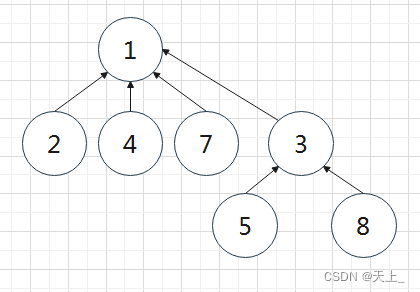
例如，有三个整数集合

S1 = {1,24,7}

S2 = {3,5,8}

S3 = {6,9,10}

存储形式采用数组

数组中每个元素的类型描述为：

typedef int ElementType;  
typedef struct
{
    ElementType Data;
    int Parent;
}SetType;

采用数组存储结点，可以通过下标访问结点，从而快速访问结点和结点信息。

双亲表示法只需要存储每个结点的父结点下标，相比于其他树形结构存储方式，双亲表示法占用的空间更小。

采用数组形式的树形结构双亲表示法存储集合结构的实现相对来说比较简单，易于理解和实现。

但是，

在使用时需要注意数组大小的限制和节点添加、删除的效率问题。此外，双亲表示法对于树形结构的高度有一定的限制，如果树的高度过高，会导致数组过大，空间利用率下降。

集合运算

查找函数

查找某个元素所在的集合（用根结点表示）

#define MAXN 1000                  /* 集合最大元素个数 */
typedef int ElementType;           /* 默认元素可以用非负整数表示 */
typedef int SetName;               /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */

SetName Find( SetType S, ElementType X )
{    /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] );  /* 路径压缩 */
}

S 数组用于存储每个元素的父结点，如果一个元素的父结点为负数，则说明该元素为集合的根。

在查找元素 X 所在的集合时，首先判断该元素是否为集合的根，如果是，则直接返回该元素的下标。

如果不是，则通过递归查找该元素的父结点，直到找到集合的根，并将路径上所有结点的父结点都设置为根结点。

在递归返回时，算法还进行了路径压缩的优化。也就是将路径上所有结点的父结点都设置为根结点，避免了后续查找时的重复递归。

路径压缩

路径压缩是一种优化技术，用于加速查找并查集中元素所在集合的过程。

在不进行路径压缩的情况下，每次查找一个元素的根结点时，需要从该元素一直向上遍历到根结点，并将路径上所有结点的父结点都设置为根结点，这样才能保证以后查找该元素所在集合时的效率。

而路径压缩技术的思想是：在递归返回的过程中，将路径上所有结点的父点都设置为根结点。假设要查找元素 X 所在的集合，从 X 开始向上查找其父结点，直到找到集合的根结点，然后将路径上所有节点的父结点都设置为根结点。这样就可以将路径上的所有结点都直接连接到根结点上，从而压缩树的高度，提高查找效率。

并运算

在进行并运算时，要注意：

元素所在集合的根结点的 S 值为负数不仅仅单纯为-1，而是用负数大小来表示集合的大小。（例如-7则表示集合中有7个元素）。

void Union( SetType S, SetName Root1, SetName Root2 )
{     /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] )  /* 如果集合2比较大 */
    { 
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else                        /* 如果集合1比较大 */
    {                         
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}

在合并两个集合时，根据两个集合的大小来判断将哪个集合并入另一个集合。这样能使得并起来之后的树的高度尽可能小一点。

如果集合 1 的大小（S[Root1]）比集合 2 的大小（S[Root2]）小，就将集合 1 并入集合 2 中。

此时，需要将集合 1 的根结点的父结点设置为集合 2 的根结点，并将集合 2 的大小增加集合 1 的大小。