1.题目来源

链表中的入口节点

2.题目描述

给定一个链表，返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

3.解题思路

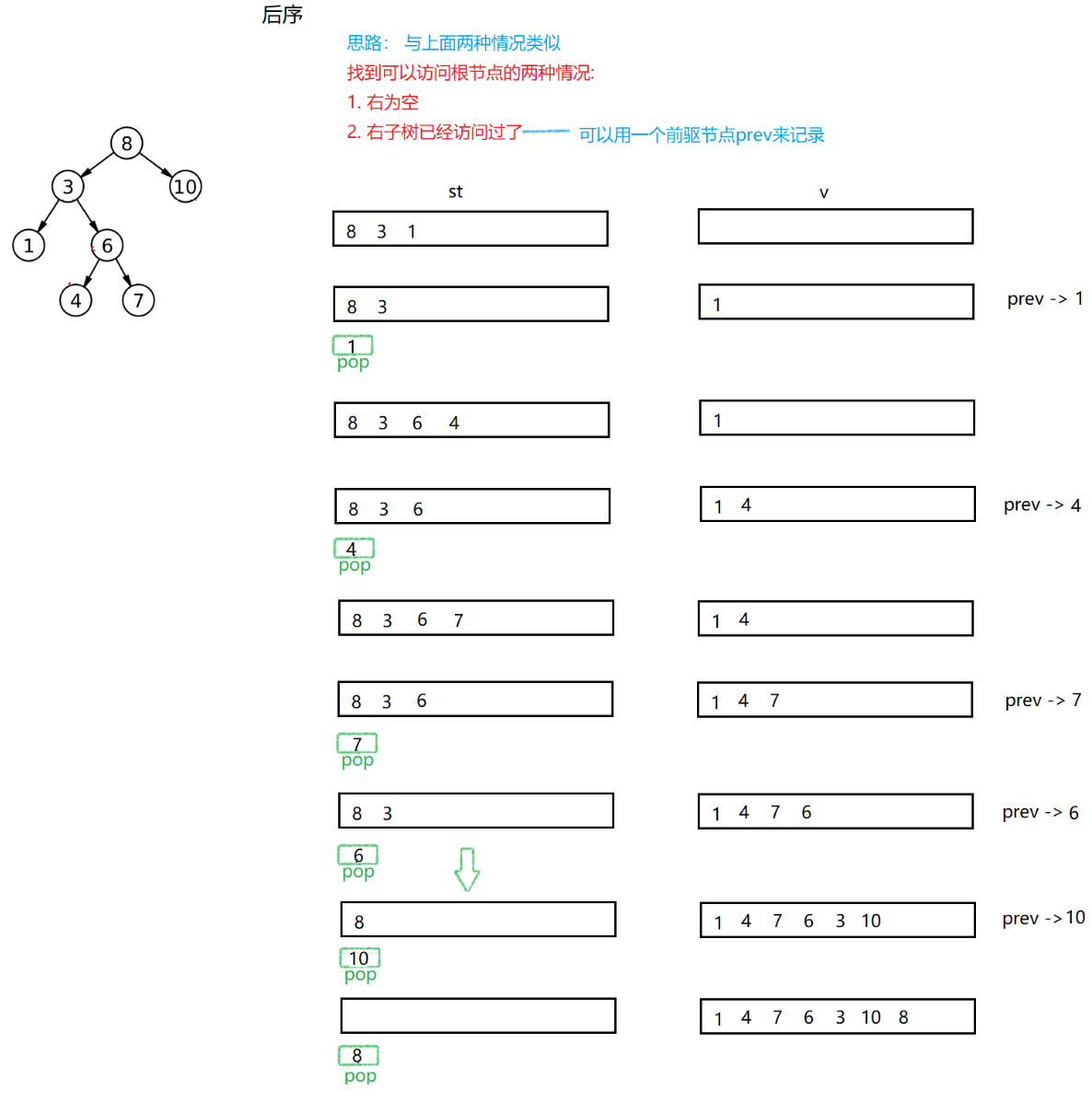
• 这里判断环的节点，我们用到了我们用到了数学上的追击问题，就是在一个圆中，两个质点同时出发，但是速度不一样，问什么时候能追上。
• 我们先讲解题思路，后讲原理。

1. 首先是证明他们存在环。我们的解题思路就是用快慢指针，慢指low针走一步，快指针fast走两步，一但他们相等了就说明他们存在环。
2. 再就是找到环的接口。这个时候我们head和low同时遍历，当head==low时就找到了环的接口。

原理：
这个时候就有人会问了为什么时选low走一步，而fast走两步，不可以是其他的比例吗？
我们先证明我们的给的这个思路是正确的。

我们先把我们的链表抽象成如图所示。


一旦他们相遇了，也就是说fast走的路程是low走到两倍。
于是我们就有一个数学表达式：2*（L+x） = L+nS+x。注意：这里为什么要用nS，是因为可能S很小，在low开始进入圆的时候fast已经走了很多圈了。化简之后就得到了：L=nS-x。

所以我们就可以从head和low同时遍历，知道相同了就是相交点。

现在来讲为什么不用其他的比例而用1比2的比例。
假如我们的比例变成了1比3，我们来探讨一下。
拿到刚才的图：

这里比例变成了1比3之后，每秒low和fast的路程之差就变成了2。
第一秒：两点距离：x-2
第二秒：两点距离：x-4
……
第n秒：两点距离：x-2^n
如果我们的x是偶数的话那么他们就会相遇。
但是如果他们x是奇数的话就不一定会相遇了。
理由：

假如我们的y是偶数的话那他们就会相遇，因为他们每一秒的差值都是2，总是会相遇的。
但是如果y是奇数的话那他们永远都不会在相遇了。因为我们知道他们每一秒的差值都是2，二我们的y又是奇数，也就是说他们在快要相遇的时候fast总是会在low的前一个单位之处，也就是又会回到上图的那种结构，往往反反总是会回到上图的样子，那他们就永远也不会相遇了。
其他比例也有类似的情况，所以我们就选用1比2的速度来判断。

4.代码展示

struct ListNode *detectCycle(struct ListNode *head) 
{
    //先判断有没有环
    //使用快慢指针
    struct ListNode *fast,*low;
    fast=low=head;
    while(fast && fast->next)
    {
        low=low->next;
        fast=fast->next->next;

        if(fast == low)
        {
            struct ListNode* meet=low;
                //在判断入环的第一个接节点
            while(meet != head)
            {
                meet=meet->next;
                head=head->next;
            }
            return meet;
        }
    }
    return NULL;

}