MATLAB实现二维稳态导热
- 一、理论基础
- 二、代码实现
一、理论基础
步骤:
Step.1 二维模型传热控制微分方程的确定,具体推导可以在任何一本传热学的书中找到。
d
2
T
d
x
2
+
d
2
T
d
y
2
=
0
\frac{d^{2}T}{dx^{2}}+\frac{d^{2}T}{dy^{2}}=0
dx2d2T+dy2d2T=0
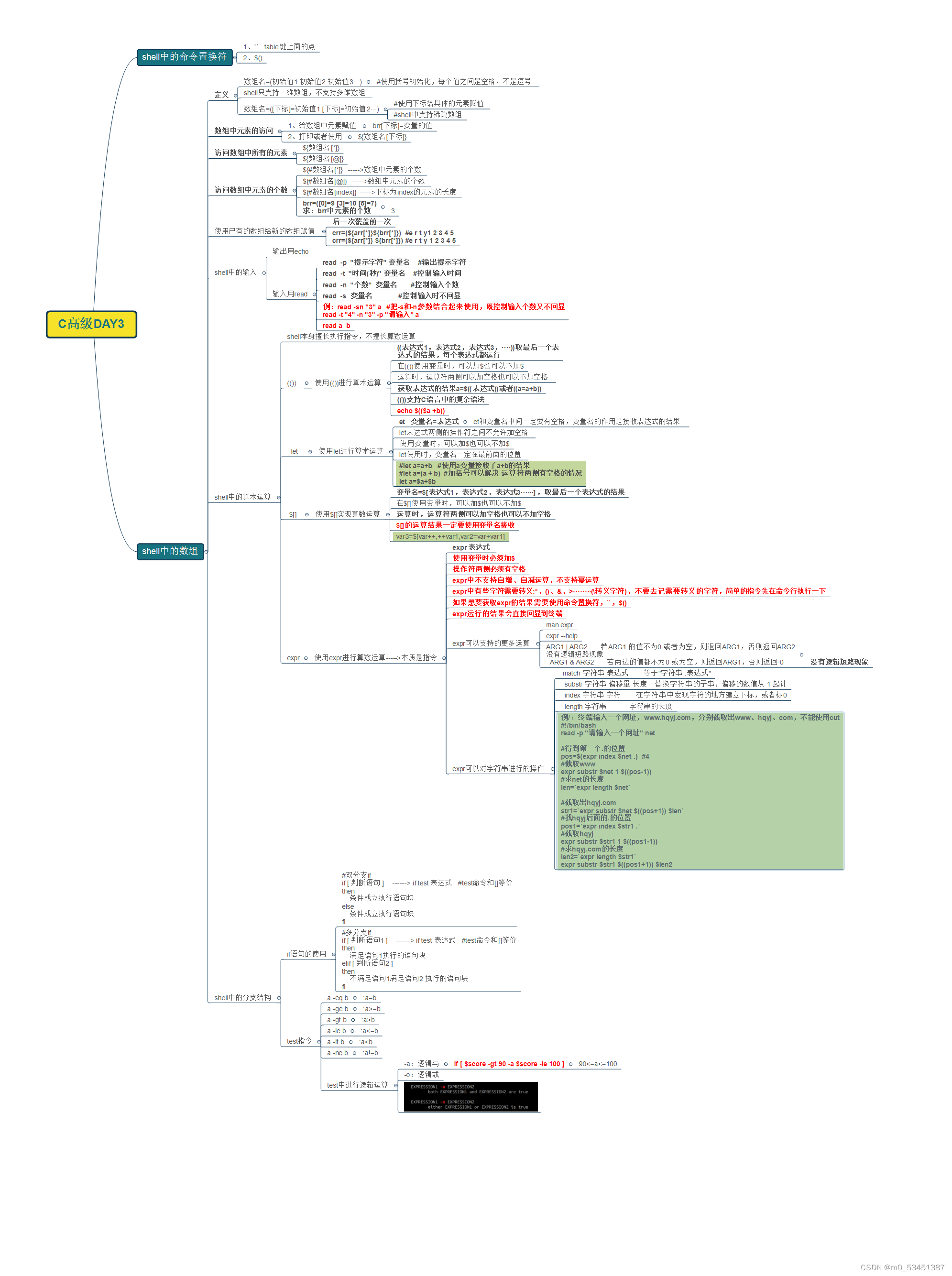
Step.2 区域离散化
绿色点: 内域网格点
红色:左侧高温边界网格点
蓝色:低温边界网格点

Step.3 微分方程转换为代数方程
T
(
i
,
j
)
=
T
(
i
+
1
,
j
)
+
T
(
i
−
1
,
j
)
+
T
(
i
,
j
+
1
)
+
T
(
i
,
j
−
1
)
4
T\left ( i,j \right )=\frac{T\left ( i+1,j \right )+T\left ( i-1,j \right )+T\left ( i,j+1 \right )+T\left ( i,j-1 \right )}{4}
T(i,j)=4T(i+1,j)+T(i−1,j)+T(i,j+1)+T(i,j−1)
Step.4 代数方程求解收敛
二、代码实现

边界条件: 左侧边界为120℃,右侧边界以及上下边界为40℃。
初始化: 中间区域初始温度为25℃。
求解方法: 采用有限差分法,误差小于1e-5时认为收敛。
% 2-D Conduction Steady state heat transfer
% finite difference method
clc; clear all;
% Geometric parameters of domin
W = 1;
H = 1;
Nx = 101;
Ny = 101;
dx = W/(Nx-1);
dy = H/(Ny-1);
% Boundary and Initial conditions
Ti = 25; % Initial temperature of domin
T = Ti * ones(Nx,Ny); % Temperature array
TL = 120; % Left wall temperature
TB = 40; % Bottom wall temperature
TR = 40; % Right wall temperature
TT = 40; % Top wall temperature
T(1,2:Ny-1) = TL;
T(2:Nx-1,1) = TB;
T(Nx,2:Ny-1) = TR;
T(2:Nx-1,Ny) = TT;
T(1,1) = (TL+TB)/2;
T(1,Ny) = (TL+TT)/2;
T(Ny,1) = (TR+TB)/2;
T(Ny,Ny) = (TR+TT)/2;
Epsilon = 1e-5;
error = 5;
% computing temperature of interior domain grid points
Iter = 0;
while (error > Epsilon)
Iter = Iter + 1;
disp(Iter);
Told = T;
for j = 2 : Ny-1
for i = 2 : Nx-1
T(i,j) = (T(i+1,j) + T(i-1,j) + T(i,j+1) + T(i,j-1))/4;
end
end
error = sqrt(sumsqr(T - Told));
disp(error);
end
% Plotting the results
x = 0 : dx : W;
y = 0 : dy : H;
colormap(jet);
contourf(x,y,T',5);
colorbar;
title('Temperature distribution','FontSize',12,'FontWeight','Bold')
xlabel('X direction[m]','FontSize',12,'FontWeight','Bold')
ylabel('Y direction[m]','FontSize',12,'FontWeight','Bold')