[蓝桥杯 2023 省 A] 填空问题

比赛的时候，脑袋要清晰一点，当时写 幸运数 这道题都感觉没在用脑子思考，花了特别多时间

A. 幸运数

小蓝认为如果一个数含有偶数个数位，并且前面一半的数位之和等于后面一半的数位之和，则这个数是他的幸运数字。例如 $2314$ 是一个幸运数字，因为它有 $4$ 个数位，并且 $2 + 3 = 1 + 4$ 。现在请你帮他计算从 $1$ 至 $100000000$ 之间共有多少个不同的幸运数字。

思路

首先，确定只有偶数位的数字满足条件；
接着，知道 $1000——10000$ 、 $100000——1000000$ 、 $10000000——100000000$ 这些范围。直接暴力由题意，取后面一半位数的数字的和与前面一半位数的数字的和作比较，相等就++ans

题解

$4430091$

B. 有奖问答

小蓝正在参与一个现场问答的节目。活动中一共有 $30$ 道题目，每题只有答对和答错两种情况，每答对一题得 $10$ 分，答错一题分数归零。

小蓝可以在任意时刻结束答题并获得目前分数对应的奖项，之后不能再答任何题目。最高奖项需要 $100$ 分，所以到达 $100$ 分时小蓝会直接停止答题。

已知小蓝最终实际获得了 $70$ 分对应的奖项，请问小蓝所有可能的答题情况有多少种？

思路

我最开始想的是至少要答 $7$ 道题，并且当有8道题及以上时，最后8道题的情况是错 对*7。除去最后8道题，剩下的题用状压枚举，并限制不能出现100分的情况
但是我一开始写的代码错了，考试的时候错了😥

题解
$8335366$

#include<bits/stdc++.h>
using namespace std;
int ans;
int main() {
	for (int i = 3; i <= 22; ++i) {
		long long t = static_cast<long long>(1) << i ;
		t -= 1;
		for (long long i1 = 0; i1 <= t; ++i1) {
			bool flag = true;
			int right = 0;
			long long t1 = i1;
			while (t1) {
				if (t1 & 1) ++right;
				else right = 0;
				if (right > 9) {
					flag = false;
					break;
				}
				t1 >>= 1;
			}
			if (flag) ++ans;
		}
	}
	printf("%d\n", ans);
}

然后加上只有 $7 、 8 、 9 、 10$ 位数时的个数，分别是 $1 、 1 、 2 、 4$ ，即可得到结果

代码原来的问题在：遇到错（也就是0），right没有变为0；if(right>9)这一句代码原来写的是if(right>=9) 😥

[蓝桥杯 2023 省 A] 平方差

给定 $L, R$ ，问 $\leq x \leq R$ 中有多少个数 $x$ 满足存在整数 $y, z$ 使得 $x=y^2-z^2$ 。

输入格式

输入一行包含两个整数 $L, R$ ，用一个空格分隔。

输出格式

输出一行包含一个整数满足题目给定条件的 $x$ 的数量。

样例输入 #1

1 5

样例输出 #1

提示

【样例说明】

$1=1^2-0^2$
$3=2^2-1^2$
$4=2^2-0^2$
$5=3^2-2^2$

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 5000$ ；

对于所有评测用例， $\leq L \leq R \leq 10^9$ 。

思路

首先肯定往数论方面靠——奇数满足 $x={(x/2+1)}^2-{(x/2)}^2$ ；
偶数：
1. ~~如果本身是平方数，那么会满足类似4=2^2-02这种~~ 第2点会覆盖这一点，所以没必要，而且加上了连40%都过不了现在发现原因了，因为我用sqrt(n)*sqrt(n)，很可能会出现数据超限。所以以后可能要尽量避免这样的代码
2. 根据自己大量的列举，发现4的倍数也满足条件
但是数据量达到10⁹，会TLE
别人的思路：转化为求[left, right]之间，是2的倍数不是4的倍数的个数ans(wer)，也就是2倍数的个数 - 4倍数的个数再用[l, r]的个数(r - l + 1)减去ans即可O(1)，也就不用遍历了🐂🍺

#include<iostream>
using namespace std;
int main(){
    int l, r, ans = 0; 
    cin>>l>>r; 
    int x = r / 2 - (l-1) / 2; 
    int y = r / 4 - (l-1) / 4; 
    ans = x - y; 
    cout<<(r - l + 1) - ans; 
}

int x = r / 2 - (l-1) / 2;
int y = r / 4 - (l-1) / 4;
这2行代码真的学习了
$r / x - (l - 1) / x = [L, R]$ 中能整除以x的数的个数

[蓝桥杯 2023 省 A] 更小的数

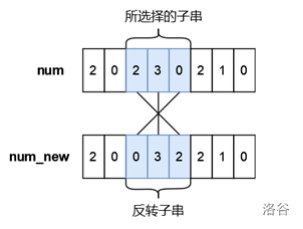
小蓝有一个长度均为 $n$ 且仅由数字字符 $\sim 9$ 组成的字符串，下标从 $0$ 到 $n - 1$ ，你可以将其视作是一个具有 $n$ 位的十进制数字 $n u m$ ，小蓝可以从 $n u m$ 中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 $num_{new}$ 满足条件 $num_{new}<num$ ，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 $n u m$ 中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是 $0$ ，这是合法的。

输入格式

输入一行包含一个长度为 $n$ 的字符串表示 $n u m$ （仅包含数字字符 $\sim 9$ ），从左至右下标依次为 $\sim n-1$ 。

输出格式

输出一行包含一个整数表示答案。

样例输入 #1

样例输出 #1

提示

【样例说明】

一共有 $8$ 种不同的方案：

所选择的子串下标为 $0\sim1$ ，反转后的 $num_{new} = 120102 < 210102$ ；
所选择的子串下标为 $0\sim2$ ，反转后的 $num_{new} = 012102 < 210102$ ；
所选择的子串下标为 $0\sim3$ ，反转后的 $num_{new} = 101202 < 210102$ ；
所选择的子串下标为 $0\sim4$ ，反转后的 $num_{new} = 010122 < 210102$ ；
所选择的子串下标为 $0\sim5$ ，反转后的 $num_{new} = 201012 < 210102$ ；
所选择的子串下标为 $1\sim2$ ，反转后的 $num_{new} = 201102 < 210102$ ；
所选择的子串下标为 $1\sim4$ ，反转后的 $num_{new} = 201012 < 210102$ ；
所选择的子串下标为 $3\sim4$ ，反转后的 $num_{new} = 210012 < 210102$ 。

【评测用例规模与约定】

对于 $20\%$ 的评测用例， $\le n \le 100$ ；

对于 $40\%$ 的评测用例， $\le n \le 1000$ ；

对于所有评测用例， $\le n \le 5000$ 。

思路

比赛的时候，真的去把字符串反转了，结果面临大量的数组越界问题，花了很多时间，估计最后也没对😥😥😥
自己重新写了一遍：尺取法——当L指向的数字比R指向的数字大时，就满足条件此时，不需要真的交换；当L指向的数字=R指向的数字时，比较此时 $[L, R]$ 区间内的数字 （比较方式同）；大于就不满足条件但是我自己写的代码过不了（在dotcpp上只过了一个测试点），自己也没找出来错误，希望有人能解答吧
别人的思路：由于题目范围是 $n \leq 5000$ ，所以可以使用 $O(n^2)$ 的做法。但是在判断大小时需要用 $O (1)$ 的方法。我们考虑用 $D P$ 。令 $f_{i,j}$ 是从 $i$ 到 $j$ 反转后是否满足要求，满足为 $1$ ，不满足为 $0$
- 若 $a_i>a_j$ ，满足要求， $f_{i,j}=1$
- 若 $a_i<a_j$ ， $f_{i,j}=0$
- 若 $a_i=a_j$ ， $f_{i,j}=f_{i+1,j-1}$

我自己的错误的代码

#include<bits/stdc++.h>
using namespace std;
int L, R;
string n;
int ans;
int main() {
	cin >> n;
	L = 0;
	R = 1;
	while (L < n.length() - 1) {
		if (R > n.length() - 1) ++L, R = L + 1;
		if (L >= n.length() - 1) break;
		if (n[L] - '0' > n[R] - '0') {
			++ans;
		}
		else if (n[L] - '0' == n[R] - '0') {
			int L1 = L + 1, R1 = R - 1;
			while (L1 < R1) {
				if (n[L1] == n[R1]) ++L1, --R1;
				else {
					if (n[L1] > n[R1]) ++ans;
					break;
				}
			}
		}
		++R;
	}
	printf("%d\n", ans);
}

正确的题解

#include <iostream>
#include <string>
using namespace std;
string a;
bool f[5010][5010];
int s=0;
int main(){
	cin>>a;
	for(int i=a.length()-1;i>=0;i--){
		for(int j=i;j<a.length();j++){
			if(a[i]>a[j]) f[i][j]=1;
			else if(a[i]<a[j]) f[i][j]=0;
			else f[i][j]=f[i+1][j-1];
			if(f[i][j]==1) s++;
		}
	}
	cout<<s;
}

[蓝桥杯 2023 省 A] 颜色平衡树

给定一棵树，结点由 $1$ 至 $n$ 编号，其中结点 $1$ 是树根。树的每个点有一个颜色 $C_i$ 。

如果一棵树中存在的每种颜色的结点个数都相同，则我们称它是一棵颜色平衡树。

求出这棵树中有多少个子树是颜色平衡树。

输入格式

输入的第一行包含一个整数 $n$ ，表示树的结点数。

接下来 $n$ 行，每行包含两个整数 $C_i,F_i$ ，用一个空格分隔，表示第 $i$ 个结点的颜色和父亲结点编号。

特别地，输入数据保证 $F_1$ 为 $0$ ，也即 $1$ 号点没有父亲结点。保证输入数据是一棵树。

输出格式

输出一行包含一个整数表示答案。

样例输入 #1

样例输出 #1

【样例说明】

编号为 $1, 3, 5, 6$ 的 $4$ 个结点对应的子树为颜色平衡树。

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 200$ ， $C_i \leq 200$ ；

对于 $\%$ 的评测用例， $\leq 5000$ ， $C_i \leq 5000$ ；

对于所有评测用例， $\leq n \leq 200000$ ， $\leq C_i \leq 200000$ ， $\leq F_i<i$ 。

思路

一开始想用链表存储树结构，再从树底向上深搜，维护每个子树需要的颜色数但碍于实力问题，我无法实现
看别人的思路 （是我没有学过的知识点）：题解

[蓝桥杯 2023 省 A] 买瓜

小蓝正在一个瓜推上买瓜。瓜推上共有 $n$ 个瓜，每个瓜的重量为 $A_i$ 。小蓝刀功了得，他可以把任何瓜劈成完全等重的两份，不过每个瓜只能劈一刀。

小蓝希望买到的瓜的重量的和恰好为 $m$ 。

请问小蓝至少要劈多少个瓜才能买到重量恰好为 $m$ 的瓜。如果无论怎样小蓝都无法得到总重恰好为 $m$ 的瓜，请输出 $- 1$ 。

输入格式

输入的第一行包含两个整数 $n, m$ ，用一个空格分隔，分别表示瓜的个数和小蓝想买到的瓜的总重量。

第二行包含 $n$ 个整数 $A_i$ ，相邻整数之间使用一个空格分隔，分别表示每个瓜的重量。

输出格式

输出一行包含一个整数表示答案。

样例输入 #1

3 10
1 3 13

样例输出 #1

提示

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 10$ ;

对于 $\%$ 的评测用例， $\leq 20$ ;

对于所有评测用例， $\leq n \leq 30$ ， $\leq A_i \leq 10^9$ ， $\leq m \leq 10^9$ 。

思路

这道题，虽然看上去就跟背包有关，但是比赛的时候想到背包也真的一点具体的思路都没有
自己下来仔细思考了一下，感觉应该要用搜索写，因为背包dp可能无法满足题目所说的把背包中的瓜刚好 $= m$ ，背包dp更多的是获取能装入的最大价值
全网暂时没找到一个能完全对的答案（很多是一个OJ能过，放到另一个OJ过不了的情况）

[蓝桥杯 2023 省 A] 网络稳定性

有一个局域网，由 $n$ 个设备和 $m$ 条物理连接组成，第 $i$ 条连接的稳定性为 $w_i$ 。

对于从设备 $A$ 到设备 $B$ 的一条经过了若干个物理连接的路径，我们记这条路径的稳定性为其经过所有连接中稳定性最低的那个。

我们记设备 $A$ 到设备 $B$ 之间通信的稳定性为 $A$ 至 $B$ 的所有可行路径的稳定性中最高的那一条。

给定局域网中的设备的物理连接情况，求出若干组设备 $x_i$ 和 $y_i$ 之间的通信稳定性。如果两台设备之间不存在任何路径，请输出 $- 1$ 。

输入格式

输入的第一行包含三个整数 $n, m, q$ ，分别表示设备数、物理连接数和询问数。

接下来 $m$ 行，每行包含三个整数 $u_i,v_i,w_i$ ，分别表示 $u_i$ 和 $v_i$ 之间有一条稳定性为 $w_i$ 的物理连接。

接下来 $q$ 行，每行包含两个整数 $x_i,y_i$ ，表示查询 $x_i$ 和 $y_i$ 之间的通信稳定性。

输出格式

输出 $q$ 行，每行包含一个整数依次表示每个询问的答案。

样例输入 #1

样例输出 #1

-1
3
5

提示

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 500$ ， $\leq 1000$ ；

对于 $\%$ 的评测用例， $\leq 5000$ ， $\leq 10000$ ；

对于所有评测用例， $\leq n,q \leq 10^5$ ， $\leq m \leq 3 \times 10^5$ ， $\leq u_i,v_i,x_i,y_i \leq n$ ， $\leq w_i \leq 10^6$ ， $u_i \neq v_i$ ， $x_i \neq y_i$ 。

思路

比赛的时候，想到的是用FLOYD算法，将 $d i s t [i] [j] = min (d i s t [i] [j], d i s t [i] [k] + d i s t [k] [j]);$ ，变成 $d i s t [i] [j] = min (d i s t [i] [j], min (d i s t [i] [k], d i s t [k] [j]));$
但是 $n≤10^5$ ，表明这个方法是错的骗分应该行，但是比赛的时候也没写对
AC思路： kruskal重构树（kruskal算法 ）

题解

#include<bits/stdc++.h>
using namespace std;

typedef long long ll; // 定义long long类型
const int N=4e5+10,M=3e5+10,K=20; // 定义常量
int n,m,q,u,v,par[N],a[N],f[N][K],dep[N]; // 定义全局变量
bool vis[N];
vector<int>E[N]; // 定义邻接表存储图
struct edge{
    int u,v,w;
}e[M]; // 定义边的结构体

int find(int x){ // 并查集
    return par[x]==x?x:par[x]=find(par[x]);
}

bool cmp(edge a,edge b){ // 边按照权值从大到小排列
    return a.w>b.w;
}

void dfs(int u,int fa){ // 用DFS求出父节点和深度
    vis[u]=1;
    f[u][0]=fa;
    dep[u]=dep[fa]+1;
    for(auto &v:E[u]){ // 遍历子节点
        if(v==fa) continue;
        dfs(v,u); // 递归调用DFS
    }
}

int lca(int u,int v){ // 求两个节点的最近公共祖先(LCA)
    if(dep[u]<dep[v]) swap(u,v); // 交换u,v的顺序使得dep[u]>=dep[v]
    int d=dep[u]-dep[v];
    for(int i=K-1;i>=0;--i){ // 用倍增预处理f数组
        if(d>>i&1)
            u=f[u][i];
    }
    if(u==v) return u;
    for(int i=K-1;i>=0;--i){ // 用倍增预处理f数组
        if(f[u][i]!=f[v][i])
            u=f[u][i],v=f[v][i];
    }
    return f[u][0];
}

int main(){
    scanf("%d%d%d",&n,&m,&q); // 读入节点数、边数和查询次数
    for(int i=1;i<=n+m;++i) par[i]=i; // 并查集的初始化
    for(int i=1;i<=m;++i) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w); // 读入边的信息
    sort(e+1,e+m+1,cmp); // 对边按照权值从大到小进行排序，便于后面的Kruskal算法
    int cur=n;
    for(int i=1;i<=m;++i){ // Kruskal重构树
        int u=e[i].u,v=e[i].v,w=e[i].w;
        u=find(u),v=find(v);
        if(u==v) continue;
        ++cur; // 新建一个点
        par[u]=par[v]=cur; // 合并两个连通块
        E[cur].push_back(u); // 新节点与原有节点建立连接
        E[cur].push_back(v);
        a[cur]=w; // 该点边权取原边的边权
    }

    for(int i=cur;i>=1;--i){ // DFS求树的深度、父节点等信息
        if(!vis[i]) dfs(i,0); // 从没有遍历的节点开始遍历
    }

    for(int j=1;j<K;++j){ // 倍增预处理f数组
        for(int i=1;i<=cur;++i) f[i][j]=f[f[i][j-1]][j-1];
    }

    while(q--){ // 处理查询
        scanf("%d%d",&u,&v);
        if(find(u)!=find(v)){ // 判断u,v是否在一个连通块中
            puts("-1"); // 不在同一个连通块中，直接输出-1
            continue;
        }
        printf("%d\n",a[lca(u,v)]); // 输出LCA的边权
    }
}

[蓝桥杯 2023 省 A] 异或和之和

给定一个数组 $A_i$ ，分别求其每个子段的异或和，并求出它们的和。或者说，对于每组满足 $\leq L \leq R \leq n$ 的 $L, R$ ，求出数组中第 $L$ 至第 $R$ 个元素的异或和。然后输出每组 $L, R$ 得到的结果加起来的值。

输入格式

输入的第一行包含一个整数 $n$ 。

第二行包含 $n$ 个整数 $A_i$ ，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

样例输入 #1

5
1 2 3 4 5

样例输出 #1

提示

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 300$ ；

对于 $\%$ 的评测用例， $\leq 5000$ ;

对于所有评测用例， $\leq n \leq 10^5$ ， $\leq A_i \leq 2^{20}$ 。

思路

我在比赛的时候，想得非常直接：异或前缀和+双指针
别人的思路：计算每一位对结果的贡献

不满分的题解

#include <iostream>
using namespace std;
int main() {
    int n;
    cin >> n;
    int a[n + 1];
    for (int i = 1; i <= n; i++) cin >> a[i];
    int preXOR[n + 1] = {0}; 
    for (int i = 1; i <= n; i++) preXOR[i] = preXOR[i - 1] ^ a[i]; 
    long long ans = 0;
    for (int i = 1; i <= n; i++) 
        for (int j = i; j <= n; j++) 
        	ans += (preXOR[j] ^ preXOR[i - 1]);
    cout << ans << endl;
}

过了一部分数据，但时间复杂度 $O(n^2)$ 过不了全部

题解

#include <bits/stdc++.h> // 引入万能头文件
#define int long long // 宏定义long long类型
using namespace std;
const int maxn = 1e5 + 10; // 定义数组最大长度
int n, ans; // 声明变量n和ans
int a[maxn]; // 声明数组a
int main() { // 主函数
    cin >> n; // 输入n
    for (int i = 1; i <= n; i++) // 循环读入数组a
        cin >> a[i], a[i] ^= a[i - 1]; // 按位异或前缀和
    for (int d = 0; d < 31; d++) { // 枚举每一位的二进制数
        int c[2] = {0, 0}; // 定义数组c，统计每种数字的个数
        for (int i = 0; i <= n; i++) // 循环遍历数组a
            ++c[a[i] >> d & 1]; // 统计当前第d位为0或1的数字个数
        ans += (1 << d) * c[0] * c[1]; // 计算当前第d位的贡献，并加入到答案中
    }
    cout << ans; 
}