【教程】用 HTML JavaScript 制作 2.5D 迷宫游戏地图

我写了一个能够随机生成迷宫的算法，得到了用户很好的反响，对大家有所帮助。我现在想将这个迷宫以2.5D游戏地图的方式呈现出来。最初我考虑使用CSS来实现这个目标，但效果并不太理想，因为我无法只将它渲染成背景，而不对整个网站进行重新排版。因此，虽然我不打算继续使用CSS来达到这个目标，但我想与大家分享如何使用CSS来按比例渲染迷宫的方法。后来，我决定使用HTML5画布功能和地图块的坐标变换来生成2.5D游戏地图。为此，我在JavaScript脚本中添加了坐标变换的脚本，分享出来希望能对大家能有所帮助。在文章的最后将把实现的地图的代码分享出来。
在这里插入图片描述

CSS 生成2.5D

使用css脚本样式将html中的div元素转换成2.5D效果，主要是通过css中的属性
在这里插入图片描述

<html>
<style>
.wrapper {
  position: fixed;
  width: 100%; height: 100%;
  left: 0; top: 0;
  text-align: center;
}
.wrapper:before {
  content: "";
  display: inline-block; vertical-align: middle;
  width: 0; height: 100%;
}
.wrapper > .grid {
  display: inline-block;
  vertical-align: middle;
}
.grid > .row {
  font-size: 0;
  width: 100px;
  white-space: nowrap;
}
.grid > .row > .cell {
  position: relative;
  display: inline-block;
  width: 10px; height: 10px;
  outline: 1px solid rgba(0, 0, 0, 0.3);
}
.grid > .row > .cell:hover {
  background-color: red;
}
.grid {
  transform: rotateX(40deg) rotateZ(45deg);
}
</style>
<body>
<div class="wrapper">
  <div class="grid">
    <div class="row">
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
    </div>
    <div class="row">
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
    </div>
    <div class="row">
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
    </div>
    <div class="row">
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
    </div>
    <div class="row">
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
      <div class="cell"></div>
    </div>
  </div>
</div>
<script>
</script>
</body>
</html>

这段代码中使用了 CSS transform 属性，它在一些较旧的浏览器（如 IE9 及更早版本）中可能不被支持。这意味着在这些浏览器中，等角视图可能无法正常显示。但是CSS又无法处理复杂交互代码中如果需要为你的网格添加更复杂的交互（如拖拽、缩放等），需要使用 JavaScript 或其他技术实现这些功能。而你的地图块的坐标的样式是写在 CSS 中的，如果你需要在运行时动态修改这些样式，可能需要使用 JavaScript 来操作 DOM，这会导致代码的复杂程度太高，最后导致无法增加其他的元素和功能到地图中来。

脚本生成地图迷宫

本文将介绍如何使用HTML5 Canvas和JavaScript来制作一个2.5D迷宫游戏地图。HTML和CSS准备工作我们需要在HTML文件中添加一个canvas元素来作为画布，然后使用CSS样式对其进行一些简单的样式设置。因为我们要在画布上绘制2.5D效果的地图，所以需要使用坐标变换函数将等角坐标系转换为屏幕坐标系和迷宫地图的生成算法。

<html>
<head>
</head>
<body>
   <style>
	canvas {
	  display: block;
	  margin: 0 auto;
	}
   </style>
  <div style="text-align: center;" id="maindiv">
     行数<input type="text" id="rowv" value="10"><button onclick="oncreate()" >生成</button>

	 <br>
    <!-- 创建一个画布，宽度为 640 像素，高度为 360 像素 -->
    <canvas width="800" height="500" id="canvas" ></canvas>
    <br>


  </div>
  <script type="text/javascript">

	// 获取画布元素
    var canvas = document.getElementById("canvas");

    // 获取画布宽度和高度
    var width = canvas.width;
    var height = canvas.height;
    // 获取画布上下文
    var context = canvas.getContext("2d");
    // 初始化格子
    var tile = [];
    var cols = 9;
    var rows = cols;

    // 等角变换的变量和辅助函数
    var IsoW = 40; // 格子宽度
    var IsoH = 20; // 格子高度
    var IsoX = width / 2; // 等角网格的中心 x 坐标
    var IsoY = 20; // 等角网格的顶部 y 坐标

    function IsoToScreenX(localX, localY) {
      // 将等角坐标转换为屏幕坐标的 x 坐标
      return IsoX + (localX - localY) * IsoW;
    }
    function IsoToScreenY(localX, localY) {
      // 将等角坐标转换为屏幕坐标的 y 坐标
      return IsoY + (localX + localY) * IsoH;
    }
    function ScreenToIsoX(globalX, globalY) {
      // 将屏幕坐标转换为等角坐标的 x 坐标
      return ((globalX - IsoX) / IsoW + (globalY - IsoY) / IsoH) / 2;
    }
    function ScreenToIsoY(globalX, globalY) {
      // 将屏幕坐标转换为等角坐标的 y 坐标
      return ((globalY - IsoY) / IsoH - (globalX - IsoX) / IsoW) / 2;
    }
	// 在给定的坐标处绘制变形倾斜45度
	function DrawIsoTile(x, y, color) {
	  // 设置填充颜色
	  context.fillStyle = color;
	  // 开始路径
	  context.beginPath();
	  // 绘制倾斜45度矩形
	  context.moveTo(x, y);
	  context.lineTo(x - IsoW, y + IsoH);
	  context.lineTo(x, y + IsoH * 2);
	  context.lineTo(x + IsoW, y + IsoH);
	  context.closePath();
	  // 填充矩形
	  context.fill();
	}

// 绘制事件
function onshow(ary) {
     canvas = document.getElementById("canvas");

    context.clearRect(0,0, canvas.width, canvas.height);
  // 循环遍历每个格子
	  for (var y = 0; y < rows; y++){
		for (var x = 0; x < cols; x++) {
		  // 获取该格子的图块和对象类型
		  var t = ary[y][x];
		  // 将等角坐标转换为屏幕坐标
		  var rx = IsoToScreenX(x, y);
		  var ry = IsoToScreenY(x, y);
		  // 绘制图块（如果有）
		  switch (t) {
		    //方格子上色，与变形倾斜45度
			case 0: DrawIsoTile(rx, ry, "#C59E77"); break;
			case 1: DrawIsoTile(rx, ry, "#94BA57"); break;
			case 2: DrawIsoTile(rx, ry, "#9DD5E2"); break;
		  }
		}
	}
}

function recursiveBacktrackingMaze(rows, cols) {
  let grid = new Array(rows);
  for (let i = 0; i < rows; i++) {
    grid[i] = new Array(cols).fill(1);
  }
  let stack = [{ row: 1, col: 1 }];
  while (stack.length > 0) {
    let current = stack[stack.length - 1];
    let neighbors = [];
    if (current.row > 2 && grid[current.row - 2][current.col] === 1) {
      neighbors.push({ row: current.row - 2, col: current.col });
    }
    if (current.col > 2 && grid[current.row][current.col - 2] === 1) {
      neighbors.push({ row: current.row, col: current.col - 2 });
    }
    if (current.row < rows - 3 && grid[current.row + 2][current.col] === 1) {
      neighbors.push({ row: current.row + 2, col: current.col });
    }
    if (current.col < cols - 3 && grid[current.row][current.col + 2] === 1) {
      neighbors.push({ row: current.row, col: current.col + 2 });
    }
    if (neighbors.length > 0) {
      let next = neighbors[Math.floor(Math.random() * neighbors.length)];
      let wallRow = (current.row + next.row) / 2;
      let wallCol = (current.col + next.col) / 2;
      grid[next.row][next.col] = 0;
      grid[wallRow][wallCol] = 0;
      stack.push(next);
    } else {
      stack.pop();
    }
  }
  // 设置入口和出口
  grid[1][0] = 0; // 入口
  grid[rows - 2][cols - 1] = 0; // 出口
  return grid;
}
function oncreate(){
    canvas = document.getElementById("canvas");
    cols = parseInt(document.getElementById("rowv").value);
	if(cols<=5){
		cols=5;
	}
	if(cols%2==0){
		cols=cols-1;
	}
    rows = cols;
    // 获取画布宽度和高度
	console.log(context);
	if(cols>12){
		canvas.width=740+(cols*45);
		canvas.height=500+(cols*30);
	}else{
		canvas.width=740;
		canvas.height=600
	}
     width = canvas.width;
     height = canvas.height;
	 IsoX = width / 2;
	 var ar=recursiveBacktrackingMaze(rows,cols);
	onshow(ar);
}
</script>
</body>
</html>

地图块坐标变化

为了将迷宫地图调整为2.5D效果，我们需要定义四个函数，它们用于将等角坐标系（isometric）与笛卡尔坐标系（screen）之间进行转换。等角坐标系常用于制作类似于 2.5D 的视觉效果。以下是各个函数的解释及示例：

// 初始化地图参数
var IsoW = 40; // 格子宽度
var IsoH = 20; // 格子高度
var IsoX = width / 2; // 等角网格的中心 x 坐标
var IsoY = 20; // 等角网格的顶部 y 坐标

function IsoToScreenX(localX, localY) {
    // 将等角坐标转换为屏幕坐标的 x 坐标
    return IsoX + (localX - localY) * IsoW;
}
function IsoToScreenY(localX, localY) {
    // 将等角坐标转换为屏幕坐标的 y 坐标
    return IsoY + (localX + localY) * IsoH;
}
function ScreenToIsoX(globalX, globalY) {
    // 将屏幕坐标转换为等角坐标的 x 坐标
    return ((globalX - IsoX) / IsoW + (globalY - IsoY) / IsoH) / 2;
}
function ScreenToIsoY(globalX, globalY) {
    // 将屏幕坐标转换为等角坐标的 y 坐标
    return ((globalY - IsoY) / IsoH - (globalX - IsoX) / IsoW) / 2;
}
// 在给定的坐标处绘制变形倾斜45度
function DrawIsoTile(x, y, color) {
    // 设置填充颜色
    context.fillStyle = color;
    // 开始路径
    context.beginPath();
	// 绘制倾斜45度矩形
    context.moveTo(x, y);
    context.lineTo(x - IsoW, y + IsoH);
    context.lineTo(x, y + IsoH * 2);
    context.lineTo(x + IsoW, y + IsoH);
    context.closePath();
    // 填充矩形
    context.fill();
}

IsoToScreenX(localX, localY)：将等角坐标转换为屏幕坐标的 x 坐标。
- 输入：等角坐标的 localX 和 localY。
- 输出：屏幕坐标的 x 坐标。
- 示例：IsoToScreenX(2, 1) 可能返回 70（具体值取决于 IsoX 和 IsoW）。
IsoToScreenY(localX, localY)：将等角坐标转换为屏幕坐标的 y 坐标。
- 输入：等角坐标的 localX 和 localY。
- 输出：屏幕坐标的 y 坐标。
- 示例：IsoToScreenY(2, 1) 可能返回 35（具体值取决于 IsoY 和 IsoH）。
ScreenToIsoX(globalX, globalY)：将屏幕坐标转换为等角坐标的 x 坐标。
- 输入：屏幕坐标的 globalX 和 globalY。
- 输出：等角坐标的 x 坐标。
- 示例：ScreenToIsoX(70, 35) 可能返回 2（具体值取决于 IsoX 和 IsoW）。
ScreenToIsoY(globalX, globalY)：将屏幕坐标转换为等角坐标的 y 坐标。
- 输入：屏幕坐标的 globalX 和 globalY。
- 输出：等角坐标的 y 坐标。
- 示例：ScreenToIsoY(70, 35) 可能返回 1（具体值取决于 IsoY 和 IsoH）。

最后，DrawIsoTile(x, y, color) 函数用于在给定坐标处绘制倾斜 45 度的矩形。这个函数接受三个参数：x 坐标、y 坐标和填充颜色。示例：DrawIsoTile(70, 35, '#FF0000') 会在屏幕坐标 (70, 35) 处绘制一个红色的等角矩形。

这里有一些关于等角投影和笛卡尔坐标系之间的转换的例子：假设 IsoX = 0, IsoY = 0, IsoW = 30, IsoH = 15。

将等角坐标 (2, 1) 转换为屏幕坐标：
- X 坐标：IsoToScreenX(2, 1) = 0 + (2 - 1) * 30 = 30
- Y 坐标：IsoToScreenY(2, 1) = 0 + (2 + 1) * 15 = 45
所以，等角坐标 (2, 1) 对应的屏幕坐标是 (30, 45)。

另外，你也可以使用 ScreenToIsoX 和 ScreenToIsoY 函数将屏幕坐标转换回等角坐标。例如，假设屏幕坐标是 (30, 45)：
- X 坐标：ScreenToIsoX(30, 45) = ((30 - 0) / 30 + (45 - 0) / 15) / 2 = (1 + 3) / 2 = 2
- Y 坐标：ScreenToIsoY(30, 45) = ((45 - 0) / 15 - (30 - 0) / 30) / 2 = (3 - 1) / 2 = 1

所以，屏幕坐标 (30, 45) 对应的等角坐标是 (2, 1)。

迷宫算法DFS

我优化了一下迷宫地图的生成方法，在原来的基础上使用了递归回溯算法的迷宫生成方式。在javascript脚本中创建一个recursiveBacktrackingMaze函数。这个算法的名称是“递归回溯法生成迷宫”（Recursive Backtracking Maze Generation）。它是一种基于深度优先搜索（Depth-First Search，DFS）的迷宫生成算法。递归回溯法通过从起点开始，随机选择一个方向移动，并创建迷宫的路径。当无法继续前进时，它会回溯到先前的路径点，直到找到新的未访问的邻居或回到起点。这个过程持续进行，直到所有可访问的单元格都被访问过。

function recursiveBacktrackingMaze(rows, cols) {
  // 创建一个空白网格，所有单元格都填充为1（墙壁）
  let grid = new Array(rows);
  for (let i = 0; i < rows; i++) {
    grid[i] = new Array(cols).fill(1);
  }
  // 初始化栈，并将起始单元格放入栈中
  let stack = [{ row: 1, col: 1 }];
  // 当栈不为空时，继续循环
  while (stack.length > 0) {
    // 获取当前单元格（栈顶元素）
    let current = stack[stack.length - 1];
    // 查找当前单元格的邻居
    let neighbors = [];
    // 检查上方邻居
    if (current.row > 2 && grid[current.row - 2][current.col] === 1) {
      neighbors.push({ row: current.row - 2, col: current.col });
    }
    // 检查左侧邻居
    if (current.col > 2 && grid[current.row][current.col - 2] === 1) {
      neighbors.push({ row: current.row, col: current.col - 2 });
    }
    // 检查下方邻居
    if (current.row < rows - 3 && grid[current.row + 2][current.col] === 1) {
      neighbors.push({ row: current.row + 2, col: current.col });
    }
    // 检查右侧邻居
    if (current.col < cols - 3 && grid[current.row][current.col + 2] === 1) {
      neighbors.push({ row: current.row, col: current.col + 2 });
    }

    // 如果有未访问的邻居
    if (neighbors.length > 0) {
      // 随机选择一个邻居
      let next = neighbors[Math.floor(Math.random() * neighbors.length)];
      // 移除墙壁（将邻居和中间单元格设为0）
      let wallRow = (current.row + next.row) / 2;
      let wallCol = (current.col + next.col) / 2;
      grid[next.row][next.col] = 0;
      grid[wallRow][wallCol] = 0;
      // 将选择的邻居添加到栈中
      stack.push(next);
    } else {
      // 如果没有未访问的邻居，从栈中弹出当前单元格
      stack.pop();
    }
  }

  // 返回生成的迷宫网格
  return grid;
}

递归回溯算法是一种深度优先搜索（DFS）算法，它从一个起始单元格开始，沿着未访问过的邻居单元格随机移动，并创建一个路径。当没有未访问的邻居时，它会回溯到先前的单元格，寻找其他未访问的邻居。这个过程将持续进行，直到回溯到起始单元格并且所有可访问的单元格都被访问过。我们需要先了解一下网格的结构和单元格的坐标。在这个算法中，网格是由奇数行和奇数列组成的，每个奇数行和奇数列上的单元格都是墙壁。这样，相邻的两个房间（即0值单元格）之间总是有一个墙壁（即1值单元格）。
让我们使用一个5x5网格来演示该算法的运行过程，并提供一些代码示例。

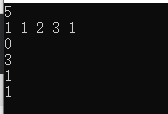
初始状态，5x5网格：

1 设置起始单元格（1,1）为0，并将其添加到栈中。

javascriptCopy codelet stack = [{ row: 1, col: 1 }];
grid[1][1] = 0;
-----------------------------------
1 1 1 1 1
1 0 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1

2 可访问的邻居生成
在递归回溯迷宫生成算法中，可访问的邻居是从当前单元格开始，沿上、下、左、右四个方向，跳过一个单元格的位置。这意味着邻居之间始终有一个单元格的距离，这个单元格是它们之间的墙壁。这就是为什么算法中的行和列索引增量是2，而不是1。
在算法中，我们首先创建一个空的邻居列表。然后，我们检查当前单元格的上、下、左、右四个方向的邻居，以确保它们在网格范围内并且尚未访问（即其值为1）。如果满足条件，我们将邻居添加到列表中。

let neighbors = [];
// 检查上方邻居
if (current.row > 2 && grid[current.row - 2][current.col] === 1) {
  neighbors.push({ row: current.row - 2, col: current.col });
}
// 检查左侧邻居
if (current.col > 2 && grid[current.row][current.col - 2] === 1) {
  neighbors.push({ row: current.row, col: current.col - 2 });
}
// 检查下方邻居
if (current.row < rows - 3 && grid[current.row + 2][current.col] === 1) {
  neighbors.push({ row: current.row + 2, col: current.col });
}
// 检查右侧邻居
if (current.col < cols - 3 && grid[current.row][current.col + 2] === 1) {
  neighbors.push({ row: current.row, col: current.col + 2 });
}
-----------------------------------
假设我们有一个5x5网格，并且当前单元格位于（1,1）
1 1 1 1 1
1 0 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1

那么可访问的邻居计算如下：

上方邻居：没有，因为它超出了网格范围。
左侧邻居：没有，因为它超出了网格范围。
下方邻居：没有，因为它是墙壁（值为1）。
右侧邻居：(1,3)，因为它在网格范围内并且尚未访问（值为1）。

所以在这个例子中，可访问的邻居列表只包含一个元素：[{ row: 1, col: 3 }]。

3 当前单元格（1,1）有一个可访问的邻居：（1,3）。选择（1,3）并移除（1,1）和（1,3）之间的墙壁。

这段代码的目的是移除两个相邻单元格之间的墙壁。为了理解这段代码，我们需要先了解一下网格的结构和单元格的坐标。在这个算法中，网格是由奇数行和奇数列组成的，每个奇数行和奇数列上的单元格都是墙壁。这样，相邻的两个房间（即0值单元格）之间总是有一个墙壁（即1值单元格）。
这里，current 是当前单元格，next 是选择的邻居单元格。由于我们在处理奇数行和奇数列，所以这两个单元格之间的距离始终是2。
因此，我们可以通过对它们的行和列分别求平均值来找到它们之间的墙壁单元格。这就是 wallRow 和 wallCol 的计算方法。接下来，我们将 next 单元格（邻居单元格）的值设为0，表示这个单元格已被访问并且成为通路。同时，我们也将 wallRow 和 wallCol 对应的单元格设为0，表示移除了墙壁，连接了 current 和 next 两个房间。

javascriptCopy codelet current = stack[stack.length - 1]; // { row: 1, col: 1 }
let neighbors = [{ row: 1, col: 3 }];
let next = neighbors[0];
let wallRow = (current.row + next.row) / 2;
let wallCol = (current.col + next.col) / 2;
grid[next.row][next.col] = 0;
grid[wallRow][wallCol] = 0;
stack.push(next);
-----------------------------------
1 1 1 1 1
1 0 0 0 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1

4 当前位置：(1,3)，向下移动，移动到(3,3) 并移除墙壁（(1,3) 和 (3,3) 之间）。
当前位置在(1,3)，接下来我们要向下移动，即沿列方向移动。首先，我们要找到下一个可移动的邻居位置。在算法中，这部分由以下代码实现：

// 查找当前单元格的邻居
let neighbors = [];
...
// 检查下方邻居
if (current.row < rows - 3 && grid[current.row + 2][current.col] === 1) {
  neighbors.push({ row: current.row + 2, col: current.col });
}

这段代码检查了下方邻居是否可达。current.row < rows - 3 确保我们不会超出网格的边界。grid[current.row + 2][current.col] === 1 确保下方邻居（距离2个单位的位置）还没有被访问过（值为1表示墙壁，也表示未访问）。如果满足条件，我们将这个邻居添加到邻居列表中。
接下来，我们从邻居列表中随机选择一个邻居作为下一个要访问的位置。这个过程由以下代码实现：

// 随机选择一个邻居
let next = neighbors[Math.floor(Math.random() * neighbors.length)];

这个例子中，我们选择了下方邻居，即(3,3)。接下来，我们需要移除当前位置(1,3)和目标位置(3,3)之间的墙壁。墙壁位于这两个位置的中间，即(2,3)。以下代码实现了墙壁的移除：

javascriptCopy code// 移除墙壁（将邻居和中间单元格设为0）
let wallRow = (current.row + next.row) / 2;
let wallCol = (current.col + next.col) / 2;
grid[next.row][next.col] = 0;
grid[wallRow][wallCol] = 0;

wallRow 和 wallCol 计算了墙壁的位置。grid[next.row][next.col] = 0; 将目标位置(3,3)设置为0，表示这是一个通路。grid[wallRow][wallCol] = 0; 将墙壁位置(2,3)设置为0，表示墙壁已经移除。
最后，将目标位置(3,3)添加到栈中，表示我们已经访问过这个位置。这由以下代码实现：

// 将选择的邻居添加到栈中
stack.push(next);

现在，我们已经从(1,3)移动到了(3,3)，并移除了它们之间的墙壁。这就是向下移动的生成过程。在迭代过程中，这个过程会不断重复，直到所有可访问的单元格都被访问。

5 当前位置：(3,3)，向左移动，移动到(3,1) 并移除墙壁（(3,3) 和 (3,1) 之间）

这些数据表示了迷宫生成过程中每个步骤的网格状态。请注意，由于算法的随机性，实际生成的迷宫可能有所不同。
如果大家有兴趣，可以改成我前面的文章中的迷宫生成算法，来生产自己的2.5D地图迷宫。