一、* 与.*
a、向量
>> a=[1 2 4];
>> b=[2 4 6];a.*b=[1*2 2*4 4*6]=[2 8 24];
注意:a 和b 的长度是一样的。
dot=1*2 + 2*4 +4*6=34 ==a*b'=34
>> a=[1 2 4];
>> b=[2 4 6];
>> a.*b
ans =
2 8 24
>> dot(a,b)
ans =
34
>> a*b'
ans =
34
矩阵
A=[1 2 3;4 5 6; 7 8 9];
B=[10 11 12;13 14 15;16 17 18];
A*B
A*B就是矩阵的乘法
Amn*Bnu=Cmu
>> A*B
ans =
84 90 96
201 216 231
318 342 366A.*B
= 1*10 2*11 3*12 =10 22 36
4*13 5*14 6*15 =52 70 90
7*16 8*17 9*18 =112 136 162
>> A.*B
ans =
10 22 36
52 70 90
112 136 162dot(A,B)

>> dot(A,B)
ans =
174 228 288* :矩阵乘法or数与数相乘
.*:点乘,用于矩阵间对应元素的相乘,或数与数之间,数与矩阵之间的相乘。
二 、\ 和/
\ 解方程

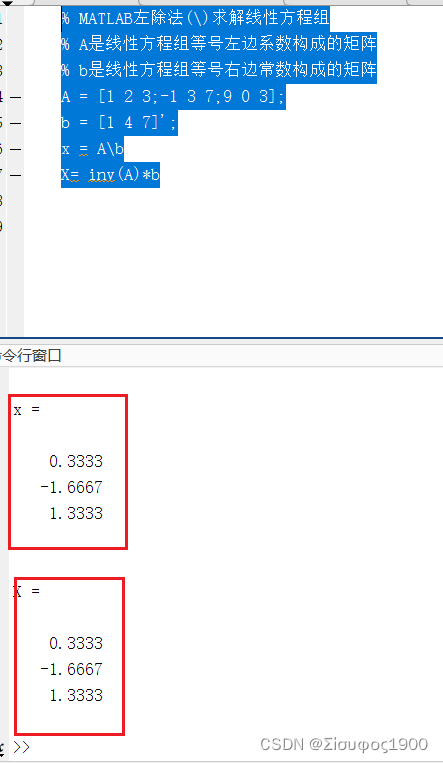
% MATLAB左除法(\)求解线性方程组
% A是线性方程组等号左边系数构成的矩阵
% b是线性方程组等号右边常数构成的矩阵
A = [1 2 3;-1 3 7;9 0 3];
b = [1 4 7]';
x = A\b
X= inv(A)*beg:
A\B=inv(A)*B;
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
b=[13,-9,6,0]';
x=A\b
C=inv(A)
X=C*b
x =
-66.5556
25.6667
-18.7778
26.5556
C =
-1.7222 1.2778 -5.4444 3.1667
0.6667 -0.3333 2.3333 -1.0000
-0.6111 0.3889 -1.2222 0.8333
0.7222 -0.2778 2.4444 -1.1667
X =
-66.5556
25.6667
-18.7778
26.5556
>> eg2
A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
B=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-1];
x=A\B
x =
1.0000 0.0000 0 9.5000
0 1.0000 0 -3.0000
0 0.0000 1.0000 2.5000
0 -0.0000 0 -2.5000/除法
向量
>> A=[ 1 2 3];
B=[2 4 6];
X=A/B
X =
0.5000
A/B =norm(A)/norm(B) *cos<A,B>矩阵
A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
B=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-1];
x=A/B
x =
1.0000 0 0 0
0 1.0000 0 0
0 0 1.0000 0
0.8667 -0.3333 2.9333 -0.4000
>>
A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
B=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-1];
x=A/B
C=inv(B)
X=A*C 
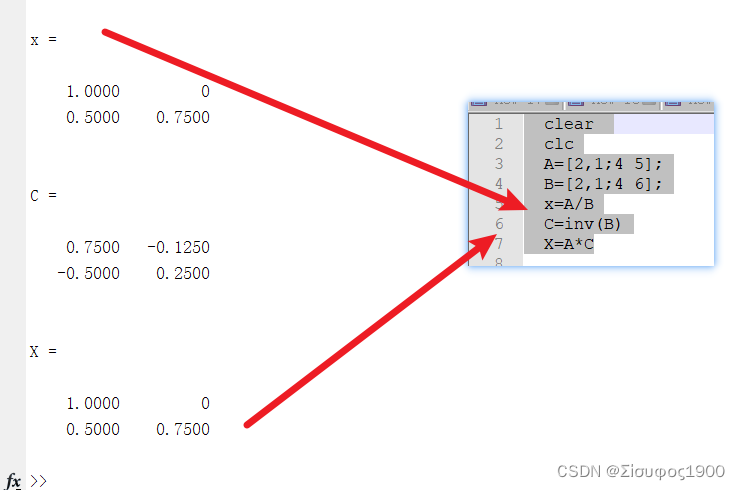
eg2:
clear
clc
A=[2,1;4 5];
B=[2,1;4 6];
x=A/B
C=inv(B)
X=A*C
/ :右除。a/b表示矩阵a乘以矩阵b的逆
\ :左除。a\b表示矩阵a的逆乘以b。
三、./ 和.\
矩阵和向量都是一样的
clear
clc
A=[1,1;2 5];
B=[2,1;4 6];
x=A./B
X=A.\B
x =
0.5000 1.0000
0.5000 0.8333
X =
2.0000 1.0000
2.0000 1.2000
>> ./ :右除。a./b表示矩阵a中的每个元素除以矩阵b的对应的元素。
.\ :左除。a.\b表示矩阵b中的每个元素除以矩阵a的对应的元素。