DP
- 一、经典问题
- 1、编辑距离
- 2、扔鸡蛋问题
- 3、整数背包
- 4、最大独立集
- 5、最长公共子序列
- 6、最长公共递增子序列
- 7、最长公共子串(ing)
- 8、最长上升子序列
- 9、最长回文子序列
- 10、最长回文子串(ing)
- 11、最长不重复子字符串(ing)
- 12、矩阵链乘(ing)
- 13、最大正方形子矩阵(ing)
- 14、最长链对(ing)
- 15、最大递增子序列和(ing)
- 16、最优二叉搜索树(ing)
- 17、回文分割(ing)
- 18、最大两段子段和(ing)
- 19、最大M子段和(ing)
- 20、最长有序子序列(ing)
- 二、高级DP技术
- 三、练习例题
- 1、POJ 1222 EXTENDED LIGHTS OUT(开关灯)
- 2、POJ 3624 Charm Bracelet(01背包)
- 3、POJ 1088 滑雪
- 4、Leetcode 剑指 Offer 49. 丑数
- 5、POJ 1661 Help Jimmy (往下跳)
- 6、
一、经典问题
1、编辑距离
————————————————— 知识点 —————————————————
字符串 a 和 b 的编辑距离是指:将 a 最少经过 x 次操作就转变为 b,而这个 x 就是 a 和 b 的编辑距离。
其中允许的操作有:在任意位置增加 / 删除 / 替换 一个字符。
(当然,将 a 变成 b 和将 b 变成 a 所需要的最少操作次数是相同的)
举例:
kitten 和 sitting 的编辑距离就是 3,因为最少需要以下操作:
1.kitten → sitten (substitution of ‘s’ for ‘k’)
2.sitten → sittin (substitution of ‘i’ for ‘e’)
3.sittin → sitting (insertion of ‘g’ at the end).
——————————下面以 HDU 4323 Magic Number 为例 ——————————
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=4323
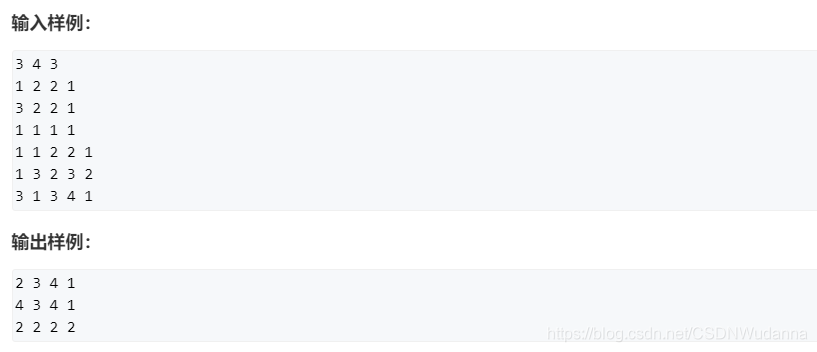
题目大意
对于 t 组测试中,每一次测试,都有 n 个纯数字字符串和 m 个查询,其中每个查询又包括一个字符串 s 和一个阈值 threshold 。问 n 个字符串中有多少个和 s 的编辑距离不超过 threshold。
(n不超过1500,m 不超过1000,threshold不超过 3 ,n个字符串的长度都小于 10,s的长度不超过10)
输入格式
t
n m
ni
mi : s threshold
输入
1
5 2
656
67
9313
1178
38
87 1
9509 1
输出
Case #1:
1
0
思路
首先,设两个字符串为 s 和 ss,我们需要明确一点的是,无论是选择 s 转变成 ss,还是 ss 转变成 s ,编辑距离是相同的,因为它们两是在相同位置做出了改变,只不过可能替换的字符不一样,但是我们只关注操作次数,对于具体怎么操作并不关心。
那么现在我们先设出dp的含义,对于 dp [ i ] [ j ],意义在于要想将 ss 的前 j 个字符转变成和 s 的前 i 个字符一样需要的最少操作次数。
那么现在就可以分类讨论啦:
- s [ i - 1 ] == ss [ j - 1 ],dp [ i ] [ j ] = dp [ i - 1 ] [ j - 1 ]
- s [ i - 1 ] != ss [ j - 1 ],则有:
dp [ i ] [ j ] = min {dp [ i - 1 ] [ j ] + 1, dp [ i ] [ j - 1 ] + 1, dp [ i - 1 ] [ j - 1 ] + 1 }
min 里面依次代表增加、删除、修改操作。
当然,我们需要处理一下边界情况才能开始dp,不难写出边界为:
dp [ i ] [ 0 ] = i
dp [ 0 ] [ j ] = j
(i、j 都是从 0 开始,当然需要注意的是,这里的 i 和 j 是指字符串前几个字符,所以字符串索引需要对 i 和 j 减一)
走的弯路
一开始我想岔了,在不超过threshold那里写状态转移,觉得操作 i 次就是在操作 i - 1 次的基础上再操作 1 次,但问题就在于操作的方式虽然只有增删改 3 种,但是操作的位置需要不断枚举,而且这样的话还需要开一个哈希存下每一轮操作后各个字符串是否被用过,再开一个队列去存下上一次操作留下的字符串,况且threshold最大也就只有 3 而已,吃力不讨好,这样下来感觉不太像是经典dp的样子hhhhhhhh
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
char book[1600][15];
char s[15];
int dp[20][20];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t;
rit;
for (int i = 1; i <= t; ++ i) {
int n, m;
sc("%d %d",&n, &m);
getchar();
//读入 n 个字符串
for (int j = 0; j < n; ++ j) {
sc("%s", book[j]);
getchar();
}
pr("Case #%d:\n", i);
//对于 m 个查询,依次给出结果
while (m --) {
memset(s, 0, sizeof(s));
int threshold;
sc("%s %d", s, &threshold);
getchar();
int cnt = 0, length_k = strlen(s);
for (int i = 0; i < n; ++ i) {
memset(dp, 0, sizeof(dp));
int length_j = strlen(book[i]);
//处理边界
for (int j = 0; j <= length_j; ++ j) dp[j][0] = j;
for (int k = 0; k <= length_k; ++ k) dp[0][k] = k;
//开始dp
for (int j = 1; j <= length_j; ++ j) {
for (int k = 1; k <= length_k; ++ k) {
if (book[i][j - 1] == s[k - 1]) dp[j][k] = dp[j - 1][k - 1];
else {
dp[j][k] = min(min(dp[j - 1][k - 1] + 1, dp[j - 1][k] + 1), dp[j][k - 1] + 1);
}
}
}
//判断是否满足要求
if (dp[length_j][length_k] <= threshold) ++ cnt;
}
//输出
pr("%d\n", cnt);
}
}
return 0;
}
2、扔鸡蛋问题
—————————————————— 知识点 ——————————————————
有这么一个极为经典的问题:有一栋 100 层的楼和 2 个完全一致的鸡蛋,现在要测试鸡蛋的硬度,问最少的测试次数。
所谓的硬度就是假如这颗鸡蛋从第 i 层楼丢下去没碎,但是从第 i + 1 层楼丢下去碎了,那么 i 就是其硬度。
一开始我很想当然的那就二分呀,每一次对楼层区间取半就好了呀,但问题就在于,最坏的情况下,我们需要 log 100(2为底) 颗鸡蛋 ,因为这和在区间二分求值不一样,鸡蛋碎了就不能再用了。
所以对于最坏的情况,借用二分,我们也只是能做到先在第 50 层扔一颗碎了以后,从第 1 层到第 49 层依次用最后一颗鸡蛋进行测试,假如在第 38 层碎了,那么它的硬度就是 37。
那么可以计算到我们最坏情况下,至少需要测试 1 + 49 = 50 次。那么有没有什么方法可以在同样最坏的情况下,拥有更少的测试次数呢?
在这里我们可以反向思考:设在最坏情况下,我们只拥有 2 颗鸡蛋情况下,最少只需要测试 x 次。
那么现在我们可以在第 x 层先扔下第一颗鸡蛋,有两种可能:
① 鸡蛋碎了
那么这个时候我们只需要从第 1 层到第 x - 1层逐层测试剩下的最后一颗鸡蛋即可,所以该情况下,我们总共只需要测试 1 + (x - 1) = x次,这和我们对于 x 的设定完全一致。
② 鸡蛋没碎
鸡蛋如果没碎,那么我们就只剩下 x - 1次测试机会和 2 颗完好的鸡蛋,这一次我们选择在第 x 层上方的第 x - 1层扔鸡蛋,即在第 2 * x - 1层扔鸡蛋。为什么呢?
因为这时候如果在 2 * x - 1层扔下去:
鸡蛋碎了,就只需要在第 x + 1 层到第 2 * x - 2 层之间逐层测试,最坏情况下总共的测试次数 = 1 + 1 + (2 * x - 2) - x = x 次,与假设一致;
鸡蛋没碎,那么就还有 x - 2 测试机会和 2 颗完好的鸡蛋,下次就再往高 x - 2 层楼的地方扔下去,以此类推。
综上,我们最坏情况下,满足 x + (x - 1) + (x - 2) + …… + 2 + 1 = 100,对 x 向上取整得到 x = 14。
(当然,要能明白此处的 x 是指最坏情况下的最少操作次数,不考虑运气好刚好投在 i 层没摔坏投在 i + 1层坏了这种情况)
那么这里还有一个推广问题,那就是假如现在是问在 M 层楼、拥有 N 颗鸡蛋,最坏情况下的最少操作次数。
显然,在 N 不为 2 的时候,上面推出来的方程就不适用了,但是分类讨论的思想是可以借鉴学习的。
————————————— 下面以 POJ 3783 Balls 为例 ————————————
原题链接:http://poj.org/problem?id=3783
题目大意
问在 M 层楼、拥有 B 颗玻璃球,测试玻璃球硬度的最坏情况下的最少操作次数。
输入格式
测试组数 t
第几个测试 B M
输出格式
第几个测试 最少操作次数
输入
4
1 2 10
2 2 100
3 2 300
4 25 900
输出
1 4
2 14
3 24
4 10
思路
这道题和经典的 100 层楼 2 个鸡蛋的本质区别在于,鸡蛋数目不唯一了(楼的层数影响不大),对应的 x 不一定是以 x 、x - 1 、x - 2……变化。
这里和钓鱼那道题暴力枚举可能停留的湖一样,这里我们也可以通过枚举 x 得到结果。
首先 dp [ i ] [ j ] 的意义在于:有 i 层楼、 j 个玻璃球,最坏情况下的最少操作次数。
那么首先,我们需要假设在已知 x 的前提下,最坏情况的最少操作次数 maxx = max(dp[ i - x ] [ j ], dp [ x - 1 ] [ j - 1 ] ) + 1。
但是这里得到的 maxx 只是在当前 x 取值下得到的,x 的取值范围为 [ 1,i ],我们还需要从 1 开始枚举 x,将每一次得到的 maxx 都和 dp [ i ] [ j ] 取最小值 ,即:dp [ i ] [ j ] = min (dp [ i ] [ j ] , maxx)。
综上,dp [ i ] [ j ] = min ( dp [ i ] [ j ] , max ( dp [ i - x ] [ j ], dp [ x - 1 ] [ j - 1 ] ) + 1) ; (x ∈ [ 1,i ])
(通俗一点来说,max 是因为要考虑到最坏情况,min 是因为要考虑到最优策略,所以才需要 “ 所有的最大里面的最小 ” )
当然,下面的代码空间复杂度是 O(M * B),实际上可以降到更少,因为每一次 dp 只需要遇到上一行的数据,但为了方便后面回顾(偷懒 √ ) ,这里就不再优化。
代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
int dp[1010][60];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t;
rit;
while (t --) {
//输入
int num, B, M;
sc("%d %d %d", &num, &B, &M);
//初始化 + 定义边界
memset(dp, INF, sizeof(dp));
for (int i = 1; i <= B; ++ i)
dp[1][i] = 1, dp[0][i] = 0;
for (int i = 1; i <= M; ++ i)
dp[i][1] = i, dp[i][0] = 0;
// dp过程
for (int i = 2; i <= M; ++ i) {
for (int j = 2; j <= B; ++ j) {
int maxx;
for (int x = 1; x <= i; ++ x){
maxx = max(dp[i - x][j], dp[x- 1][j - 1]) + 1;
dp[i][j] = min(dp[i][j], maxx);
}
}
}
//输出
pr("%d %d\n", num, dp[M][B]);
}
return 0;
}
3、整数背包
—————————— 下面以 HDU 2602 Bone Collector 为例 ——————————
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2602
题目大意
有 n 块骨头,一个容积为 v 的背包, 已知每一块骨头各自的体积和价值,问在不超过背包能容纳的范围内,背包内能承载的最大价值。
输入格式
测试样例组数 t
n v
每一块骨头的价值
每一块骨头的体积
输出格式
最大价值
输入
1
5 10
1 2 3 4 5
5 4 3 2 1
输出
14
思路
dp [ i ] [ j ] 的含义是在前 j 块骨头中拿不超过容积 i 的最大价值。
首先,对于第 i 块骨头,我们可以选择拿或者不拿,如果不拿,那么 dp [ i ] [ j ] = dp [ i ] [ j - 1 ];假如将这块骨头拿下(不超过v为前提),那么 dp [ i ] [ j ] = max(dp[ i ] [ j ], dp[i - 这块骨头的体积 ] [ j - 1] + 这块骨头的价值)。
很悬的是,这道题需要考虑骨头重量为 0 的情况……
代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
int dp[1010];
int value[1010];
int V[1010];
int main() {
// freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t;
rit;
while (t --) {
int n, v;
sc("%d %d", &n, &v);
for (int i = 1; i <= n; ++ i) {
sc("%d", &value[i]);
}
for (int i = 1; i <= n; ++ i) {
sc("%d", &V[i]);
}
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; ++ i) {
//必须是大于等于 0 (虽然我也搞不懂为什么需要考虑骨头重量 == 0)
for (int j = v; j >= 0; -- j) {
if (V[i] <= j) {
dp[j] = max(dp[j], dp[j - V[i]] + value[i]);
}
}
}
pr("%d\n", dp[v]);
}
return 0;
}
4、最大独立集
(悄咪咪说一句 好像不是dp, 但是是目前学最久收获挺多的一道题了,一开始hhhh一直列不出来dp[ G ] [ B ] 怎么转移,后面犟太久了顶不住看了题解,发现需要学二分图、最大匹配、匈牙利算法,听都没听过……我两行清泪流下来,为什么当初要犟那么久才看题解)
————————————————— 知识点 —————————————————
这道题我主要是学了下面这篇博客,真的写的超级好,每一步都很细致,通俗易懂又深入浅出 nice~
夜深人静写算法(八)- 二分图最大匹配:https://blog.csdn.net/WhereIsHeroFrom/article/details/112479644
下面贴一些和这道题有关的概念和结论:
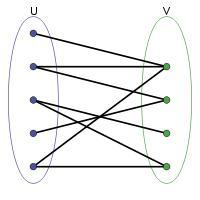
1、二分图:
二分图简单来说就是一个图的所有点可以分成两个独立的集合U、V,这里所谓的独立是指集合 U 所有点之间都没有边相连,V 也同理。但是 U 和 V 之间可能会有边相连。
比如下图:
2、匹配
定义:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 E 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
简单来说就是假如 M 中有 a 到 b 的关系,那么 M 中就不能有任何其它以 a 或者 b 为端点的边。
从匹配的定义可以看出,匹配也是一个图,并且图中的 点数 是 边数 的 2 倍;
3、最大匹配
定义:最大匹配就是找到一个子图,满足是匹配,并且边数(点数)最多。
(一般用匈牙利算法求出)
4、匈牙利算法
(后面的例题是该算法的一个模板)
简单来说,这就是一个讲究时间顺序、对渣男横刀夺爱、对好男人忍痛割爱的爱情故事。
在一个美丽的小镇上,有一群单身男女,他们碍于当时落后的思想,不敢积极主动追求爱情,但是随着新思想不断涌进,他们也日渐开放起来(这里默认是只有男生追女孩子),敢于对平时有好感的异性展开追求(都说了是美好的小镇了,所以我们默认追了就能追到手)。
但我们也知道,爱情是分先来后到的,总会有人比你先勇敢一步,也就是最前面所说的 “ 讲究时间顺序 ”,那么我们假设这个小镇有 4 个男生 5 个女生,对他们分别编号b1、b2、……,g1、g2……(boy 和 girl 的意思),其中 b1、b2……是按照谁先勇敢谁就排在前面的规则排序。
虽然小镇美好,但是人不一定都是好人,一个男生他可能同时对多个女生有好感,现在我们将男女的好感关系列出来(有连线即彼此互相有感觉):

现在有一个 “ 好朋友 ” 聚会,顾名思义,参加聚会的人不能有超过朋友以上的情感,换句话说,参加聚会的人在上面的关系图中不能存在边相连。现在想问,这个小镇最多有多少人能参加?
问题的答案就是男生数量 + 女生数量 - 该二分图的最大匹配数。因为对二分图去掉最大匹配中每一个匹配的一个端点,最终得到的二分图就是最多顶点且没有任何边相连的子图,而这个子图我们称之为最大独立集。
为什么是“ 男生数量 + 女生数量 - 该二分图的最大匹配数 ” 呢?我们可以反证:假如我们现在已经得到了最大匹配数,根据最大匹配数的定义,此时但凡再多加一条边,都会使得最大匹配不成立,而且增加的边必定有一个端点包含于原先的最大匹配中,那么这条新加的边完全可以靠去除那个相同的端点而一同去除,没有必要再多加一条边进来。
好,那么现在我们再解决一个为什么是只减去该二分图的最大匹配数,而不用 * 2 呢?一条边的两个端点一起去除不是更保证没关系吗? 这是因为要想消除最大匹配里面的所有边,只需要把一个端点去掉,那么两个端点之间的边也会跟着消除,不必要两个端点同时消失,因为我们要求的是最大独立集,当然是想要满足要求的点最多。
用上面那个故事来说就是,我们把最大数量能参加好朋友聚会的男男女女当成那个最大独立集,因为该集合下,没有任何一个人对另一个有好感。而上面所谓的最大匹配就对应于这个小镇最多能有几对终成眷属,对应那个二分图,就是 b1 - g3、b2 - g5、b3 - g1,此时最划算,因为能凑成最多对情侣,那么我们也由此可以发现,只要去除了 b1、b3、g5 这 3 个人,那么剩下的就是最多人参加聚会的人。(不一定是全去除左端点或者全去除右端点,就像这个例子一样。不过这不影响,因为每条匹配只需要去掉一个端点就行了,至于去掉的是哪个端点,并不影响结论)。
好,罗里吧嗦讲完了,那么在代码上这个集合怎么求呢?
还记得我们一开始说这是一个讲究时间顺序、对渣男横刀夺爱、对好男人忍痛割爱的爱情故事吗?横刀夺爱和忍痛割爱我个人感觉hhhhhh就是匈牙利算法的精髓hhhhhhh。(把上面的图再放一遍)

是这样子的,男生 b1,是男生中最先主动的人,那么现在他追到 g1 了,两个人谈起了甜甜的恋爱;
第二个主动的是 b2 ,刚刚好,他主动的也还算早,g5 还单身,所以他也追到了,b2 也和 g5 谈起了恋爱;
但是 b3 就太闹心了,喜欢也不主动点,他发现 g1 已经和 b1谈起了恋爱,但是他又只喜欢 g1, 所以没有办法劝自己下一个更乖悄然离去,而且很重要的一点是,他发现 b1 很渣,虽然和 g1 谈恋爱,但是同时和 g3、g4 搞暧昧,g1 已经因为这些事和他吵了很多次了,于是 b3 就觉得,哎呀机会来了!趁着两个人冷战 b1 去找 g3 诉苦,b3 也去听 g1 诉苦,一来二往,b3 就横刀夺爱和 g1 在一起了,而渣男 b1 也和 g3 在一起了,至此男生 1 2 3号都有了对象啦;
接下来就到最后一颗独苗了, 可是 b4 刚想迈出那一步,结果发现已经被 b2 捷足先登了!而且 b2 是个专一的人,他并没有机会下手,于是就忍痛割爱,为自己的慢一步买单去了。
到这里我们可以发现,为什么 b3 能得手,b4 不能?因为假如 b3 和 g1 在一起了,b1 可以找别人,换句话说,这样做能增加情侣的对数。而就算 b4 最终从 b2 手中抢下 g5,也没有其他女生能和 b2 匹配,总的情侣对数并不会增加,倒不如退一步成人之美是吧。
而这里得到的最多情侣对数就对应于我们想求的最大匹配数,有了最大匹配数,最小顶点覆盖、最大独立集就套公式可以求出。
5、最小顶点覆盖
定义:选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖整张图所有的边。
结论:二分图最小顶点覆盖 = 二分图最大匹配
6、最大独立集
定义:选取最多的点,使得选中的点在图中任意两点都没有关系。
结论:二分图的最大独立集 = 顶点总数 - 最小顶点覆盖 = 顶点总数 - 二分图最大匹配。
——————————下面以 HDU 2458 Kindergarten 为例 ——————————
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2458
题目大意
幼儿园有一个班,班上有 G 个女生、B 个男生,其中女生两两之间互相认识,男生也是两两认识。男生编号 1 、2、……,女生同理。现在存在 M 对关系,关系 1 - 2 指女生1 和男生2认识。问该班上最多有几个人两两之间互为认识。
G、B、M 皆不超过 200。
输入格式
G B M
M行……
0 0 0 输入结束
输出格式
Case 1: 答案
……
输入
2 3 3
1 1
1 2
2 3
2 3 5
1 1
1 2
2 1
2 2
2 3
0 0 0
输出
Case 1: 3
Case 2: 4
思路
显然,a 和 b 认识,b 和 c 认识并不能推出 a 和 c 认识,所以这道题不能用并查集。但是 女女、男男之间互相认识,如果把女生男生各自当成一个点集,显然不能构成二分图。但是因为我们是要求两两认识的最大数,那么我们就是要把不认识的最大匹配数求出来,那么 男 + 女 - 不认识的最大匹配数 = 认识的最大独立集。
所以基于上面对最大独立集求法的分析,我们按照建图 - 匈牙利算法求最大匹配 - 输出顺序完成。
代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
bool graph[210][210]; //图
int pre[210]; //匹配
bool book[210]; //判断当前的男生是否遍历过
int g, b, m;
//找看看能不能增加匹配数,能 - true,不能 - false
bool findMatch(int k) {
for (int i = 1; i <= b; ++ i) {
// if(两个人认识 && 当次还没遍历过的男生)
if (graph[k][i] == false && book[i] == false) {
book[i] = true; //true表示当次不必再在i号男生查询
//if(直接匹配 || 让原先和i号男生匹配的女生找别的男生匹配)
if (pre[i] == 0 || findMatch(pre[i])) {
pre[i] = k; //更新和i男生匹配的女生
return true; //能增加匹配数
}
}
}
return false; //不能增加匹配数
}
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t = 1;
while (sc("%d %d %d", &g, &b, &m) != -1 && g + b + m > 0) {
//置零
MEM(graph, false);
MEM(pre, 0);
//建图
int x, y;
for (int i = 0; i < m; ++ i) {
sc("%d %d", &x, &y);
graph[x][y] = true;
}
///计算最大匹配
int cnt = 0;
for (int i = 1; i <= g; ++ i) {
//每一次匹配,都应当对男生重置,因为从头到尾把男生走一遍才能确保不会漏
MEM(book, false);
if (findMatch(i))
++ cnt;
}
//输出
pr("Case %d: %d\n", t ++, g + b - cnt);
}
return 0;
}
5、最长公共子序列
————————————————— 知识点 —————————————————
最长公共子序列(LCS)通常指两个字符串在各自去掉一些字符(可以不连续,但仍保持有序)后完全一致且长度最长。
——————————下面以 HDU 1243 反恐训练营 为例 ——————————

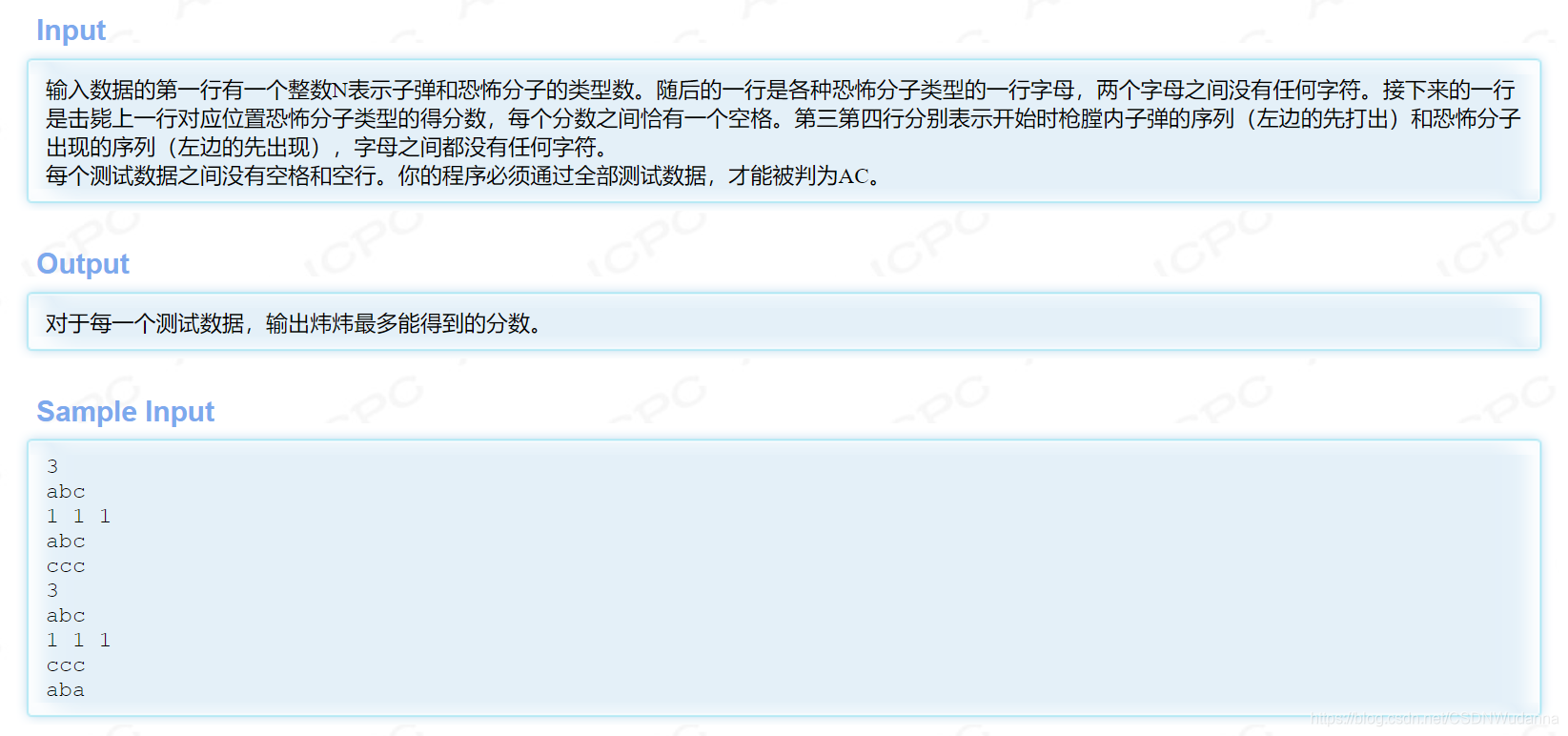
思路
dp[ i ] [ j ] 指:前 i 枚子弹在遇到前 j 名恐怖分子时能获得的最高分。
那么假如现在第 i 枚子弹能击毙第 j 名恐怖分子,那么:
dp [ i ] [ j ] = max(dp[ i - 1 ] [ j - 1 ] + value[ zi [ i - 1 ] - ‘a’ ], dp [ i - 1 ] [ j ] )
即:max(开这一枪,不开这一枪);
反之,dp [ i ] [ j ] = max(dp[ i - 1 ] [ j ], dp [ i ] [ j - 1 ])
即:max(留着子弹,放空枪)。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
int value[26];
char arr[30], zi[2010], people[2010];
int dp[2010][2010];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int n;
while (sc("%d", &n) != -1) {
getchar();
sc("%s", arr);
getchar();
int length = strlen(arr);
for (int i = 0; i < length; ++ i) {
sc("%d", &value[arr[i] - 'a']);
}
sc("%s", zi);
getchar();
sc("%s", people);
getchar();
int i_length = strlen(zi), j_length = strlen(people);
for (int i = 0; i <= i_length; ++ i) dp[i][0] = 0;
for (int i = 0; i <= j_length; ++ i) dp[0][i] = 0;
for (int i = 1; i <= i_length; ++ i) {
for (int j = 1; j <= j_length; ++ j) {
if (zi[i - 1] == people[j - 1]) {
dp[i][j] = max(dp[i - 1][j - 1] + value[zi[i - 1] - 'a'], dp[i - 1][j]);
// dp[i][j] = dp[i - 1][j - 1] + value[zi[i - 1] - 'a'];
}
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
pr("%d\n", dp[i_length][j_length]);
}
return 0;
}
6、最长公共递增子序列
顾名思义,求两个序列能递增的最长相同子序列,比如说序列 s 是 -1 5 7 -2 8 9,序列 ss 是 -8 -1 7 10 9,那么他们的最长公共递增子序列是 -1 7 9,既要递增,又要保持原来的相对顺序不变。
—————下面以 HDU 1423 Greatest Common Increasing Subsequence 为例 —————
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=1423
题目大意
给定 t 组数据,每一组都给出两个序列,求最长公共递增子序列。
样例
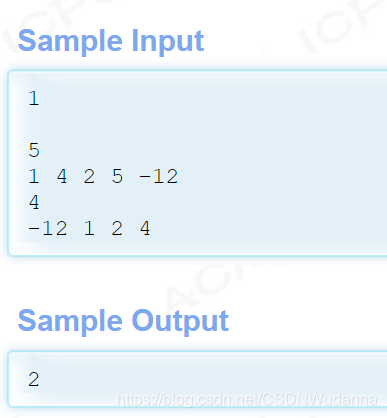
代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
//dp[j] 表示此时和第二个序列的前j个数所能构成的最长公共子序列长度
int arr1[510], arr2[510], dp[510];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t;
rit;
while (t --) {
int n, m;
rin;
for (int i = 1; i <= n; ++ i) {
sc("%d", &arr1[i]);
// pr("%d")
}
sc("%d", &m);
for (int i = 1; i <= m; ++ i) sc("%d", &arr2[i]);
MEM(dp, 0);
for (int i = 1; i <= n; ++ i ) { //代表序列arr1
int flag = 0;
for (int j = 1; j <= m; ++ j) { //代表序列arr2
if (arr2[j] < arr1[i] && dp[j] > dp[flag])
flag = j; //寻找小于arr1[i]的子序列最长的arr2[j]
else if (arr1[i] == arr2[j])
dp[j] = dp[flag] + 1;
}
}
int ans = 0;
for (int i = 0; i <= m; ++ i)
ans = max(ans, dp[i]);
pr("%d\n", ans);
if (t) pr("\n"); //题目没说明,但是需要用空行隔开
}
return 0;
}
7、最长公共子串(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
8、最长上升子序列
————————————————— 知识点 —————————————————
——————————下面以 HDU 1257 最少拦截系统 为例 ——————————
题目
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=1257

解法一:dp
1、思路
先说结论:这道题可以用最长上升子序列反求最长不增子序列的最大数目,因为最长上升子序列中的任意两个导弹都不可能会存在同一个系统中,而不在这个序列中的其他导弹都至少能和序列中的一个导弹存在于同一个系统中。
简单证明一下(如有错漏 欢迎指出):
假设这个最长上升子序列为 a1、b1、c1,那么所有在 a 前面的值必定都大于等于 a (因为如果存在的话子序列的长度就不止 3 个),且在 a 前面的这些值所构成的新序列中,新的最长上升子序列必定不会大于 3,假设为 a2、b2、c2,那么类推下去 a2前面所有值构成的新序列中,新的最长上升子序列也同样不会大于 3,循环往复到 an 前面不足三个的时候,我们会发现,都不足三个值了,再怎么不济,都能接在an、bn、cn 前面,此时可以证明, an 前面并不需要增加新的系统。
同理,在 c 1后面的值也都一定小于等于 c1,和上面一样类推下去,cn 后面,不需要增加新的系统的数,因为都一定可以接在 an、bn、cn 后面。
最后就只剩下夹在 a1、b1、c1 (设为64、65、78)之间的数了。
先看 a1 和 b1 之间夹的数,对此我们可以分类讨论:
①首先夹的这些数的值不可能在 a1 ~ b1 之间,否则最长上升子序列长度不止 3;
②假如夹的数比 a1 小,那么把它们抽离出来,看成一个新序列,这个新序列的最长上升子序列不可能大于 1,不然它们可以代替 a1 从而增加最终最长上升子序列的长度。
打个比方,不可能是 64、7、15、65、78,不然完全可以是7、15、65、78 从而使得最终长度为 4。
换句话数,夹在其中的数单调不增,所以必然可以接在 a1 后面,不用增加新的系统。
③ 假如夹的数比 b1 大,和上面一样可以推出能接在 b1 前面或者可能在c1前面,不用增加新的系统。
④假如夹的数等于 a1 或者等于 b1,那直接接在 a1 后面 b1前面就好啦,不用增加新的系统。
同理,b1 和 c1 之间夹的数也可以推出不需要增加系统。
综上,一个序列中,最长上升子序列长度 == 最长不增子序列的最大数目
2、代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
//dp[i]:以第 i 个值为终点的最长上升子序列的长度
int nums[1010], dp[1010];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int n;
while (sc("%d", &n) != -1) {
MEM(dp, 0);
for (int i = 1; i <= n; ++ i) sc("%d", &nums[i]);
int ans = 0;
for (int i = 1; i <= n; ++ i) {
dp[i] = 1;
for (int j = 1; j < i; ++ j) {
if (nums[j] < nums[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
ans = max(ans, dp[i]);
}
pr("%d\n", ans);
}
return 0;
}
解法二:贪心 - 优先队列
1、思路
对于 155、389、207、300、170、64、65、7、14、78 这个例子,我们可以构建出历程如下的 3 个系统:
155、64、7
389、207、170、14、
300、78
在一开始构建出 155 的时候,389不能接在他后面,所以开了第二个系统,207只能接在 389 后面,遇到 300 又开了一个新的,依次类推。
需要注意的是,64 虽然看起来 155 和 170 后面都能接,但是为了以防后面出现一个在156 到 170 的数导致可能会增加新的不必要的系统,所以应该把 64 接在所有能接的且末尾最小的系统后面。
代码实现方面,可以开一个小根堆,堆内元素为每个系统当前末尾的那个值。
2、代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
//系统
struct sys {
int height;
bool operator < (const sys &a) const { //重载小于号
return height > a.height;
}
};
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int n;
while (sc("%d", &n) != -1) {
sys s;
sc("%d", &s.height);
priority_queue<sys> pq;
pq.push(s);
for (int i = 1; i < n; ++ i){
sc("%d", &s.height);
stack<sys> stack; //储存堆内不能接下当前导弹的系统
while (!pq.empty() && pq.top().height < s.height) {
sys temp = pq.top();
stack.push(temp);
pq.pop();
}
if (!pq.empty()) {
pq.pop();
}
pq.push(s);
//将拿出的系统放回去
while (!stack.empty()) {
pq.push(stack.top());
stack.pop();
}
}
//计算一共有多少个系统
int cnt = 0;
while (! pq.empty()) {
++ cnt;
pq.pop();
}
pr("%d\n", cnt);
}
return 0;
}
9、最长回文子序列
——————————下面以 HDU 4745 Two Rabbits 为例 ——————————
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=4745
题目大意
一个由 n 堆石头圈起来的圆,每一颗石头都有它的权值,兔子a、b在石头上面走,要求同一时刻a、b站的石头必须权值相等,问她两最多能一起走多少颗石头?
(当他们相遇了就不能再走了;可以跳着走;可以同一时刻站在同一颗石头上面;a走顺时针,b走逆时针)
样例
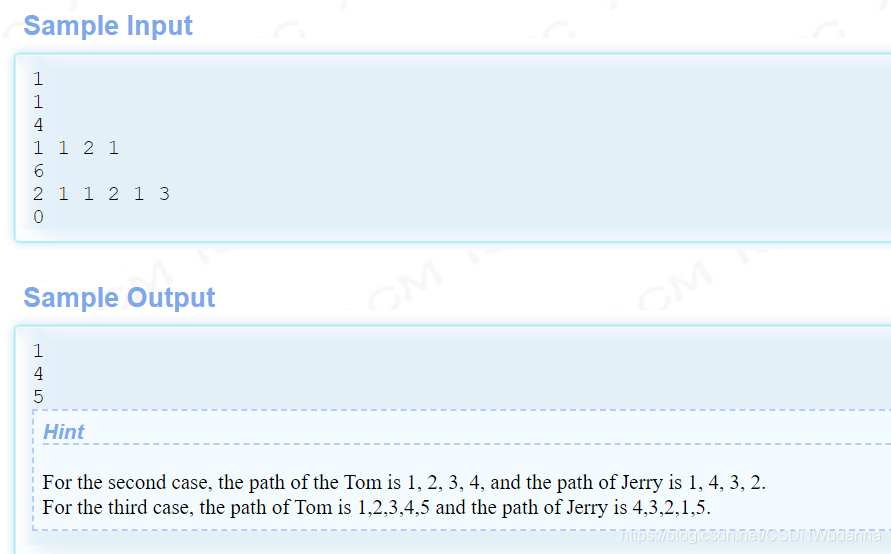
思路
首先,两只兔子走反方向,又要求石头权值相同,那么相当于是一个回文序列,这样能走的石头才能最多。
当然,设这个回文序列最少在区间 [ l ,r ] 内能找到,那么假如 r - l + 1 < n,即区间内能包含的石头(不一定全是回文序列的石头)少于 n 颗,那么也就是说,如果两只兔子在回文序列的中间开始往两边走,直到走到区间端点后,还能一起跳到一颗不属于回文序列的石头上,此时需要 + 1。
(用上面 1 1 2 1 的例子,就是 1 2 1 是最长回文序列,但是两只兔子可以都在 2 出发,都可以走 2 1 1 的路线)
即:ans = max (max(ans, dp[ i ][ i + n - 1 ]), dp[ i ][ i + n - 2 ] + 1);
代码
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 2010; //两倍长,方便表示环
//(val & 1) == 0偶, == 1奇。
int nums[N], dp[N][N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
rin;
while (n != 0) {
MEM(dp, 0);
for (int i = 1; i <= n; ++ i ) {
sc("%d", &nums[i]);
nums[i + n] = nums[i];
dp[i][i] = 1; //一颗石头本身也是回文序列
dp[i + n][i + n] = 1;
}
for (int len = 2; len <= n; ++ len) { //枚举能走的石堆的长度
for (int i = 1; i + len - 1 <= 2 * n; ++ i) { // i - 起始位置
int j = i + len - 1; // j - 终点位置
if (nums[i] == nums[j]) {
//若 i+1 > j-1,那么dp[i + 1][j - 1] = 0
dp[i][j] = dp[i + 1][j - 1] + 2;
}
else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
int ans = 0;
//回文序列囊括了整个环
for (int i = 1; i <= n; ++ i) {
ans = max(ans, dp[i][i + n - 1]);
}
// 回文序列没有囊括整个环
for (int i = 1; i <= n; ++ i) {
ans = max(ans, dp[i][i + n - 2] + 1);
}
pr("%d\n", ans);
sc("%d", &n);
}
return 0;
}
10、最长回文子串(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
11、最长不重复子字符串(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
12、矩阵链乘(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
13、最大正方形子矩阵(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
14、最长链对(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
15、最大递增子序列和(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
16、最优二叉搜索树(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
17、回文分割(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
18、最大两段子段和(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
19、最大M子段和(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
20、最长有序子序列(ing)
————————————————— 知识点 —————————————————
——————————下面以 为例 ——————————
二、高级DP技术
三、练习例题
1、POJ 1222 EXTENDED LIGHTS OUT(开关灯)
原题链接:http://poj.org/problem?id=1222
题目大意
0 表示灯暗,1 表示灯亮。
先给出 5 行 6 列 一共30 盏灯的暗灭情况,问是否存在一种开关灯的方案使得操作后所有灯都关了。
对灯的开关操作一次,该灯及其上下左右一共五盏灯的亮灭情况取反。
思路
因为一共30栈,每一盏灯都可以操作任意次,看起来像是需要 2 ^ n ^ 30,但是通过观察我们可以发现,同一盏灯,操作2次和操作4次是一样的结果,所以其实每一盏灯只有操作0次和1次的讨论必要。
但是呢,2 ^ 30 依旧会超时,我们就要想是否有更优的方法。
先看第一行,第一行一共有6盏,那么第一行其实也就 2 ^ 6 = 64 种开关方式,而无论哪一种方式,得到的第一行的亮灭情况是唯一的,而如果此时第一行还有灯亮着,那么它就只能通过下一行相同列来使得该灯灭了。所以换句话说,假如第一行情况确定,那么第二行的操作方案也是唯一确定的。进而可以推出,第三行、第四行、第五行也是唯一确定的。
所以该方案是否可行,就转换成了看第五行在一系列操作后,是否全灭了(因为1 - 4 行必定全部已灭)。
所以在先确定第一行的前提下,我们可以在最多尝试 64 次的情况下确定正确的操作方案。
在代码实现方面:
可以用 0 ~ 63 的二进制数表示第一行的操作方式,而且为了方便,我是直接用奇数代表 0、偶数代表 1。
走的弯路
1:0 1 1 0 1 0
2:1 0 0 1 1 1
3:0 0 1 0 0 1
4:1 0 0 1 0 1
5:0 1 1 1 0 0
这一道题一开始我就没考虑好全部的情况,2 ^ 30必定会超时,那么我就很想当然的觉得,对于第一行的 0 1 1 0 1 0,只有第2、3、5盏灯是亮的,那么我们就操作第二行的第2、3、5盏灯,这样就可以让第一行全部灭了。同理再让第三行操作第二行,第四行操作第三行……
但这里有一个漏洞就是,其实第一行的第2、3、5盏灯,除了让第二行的相同列去处理,还可以让第一行去处理。
比如说,对于第一行第 2 盏灯,它完全可以通过操作第一行第 1 盏灯变暗。而虽然第一行第 1 盏灯会因此亮起来,但是它可以通过第二行去调整。
所以是不可以简单粗暴按照我一开始的方式去做,应当对第一行 6 盏灯都进行 开 / 关 的讨论。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEM(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
int light[10][10];
int ways[10][10];
int nows[10][10];
//num第i位二进制数是0还是1 (i从1开始)
int get_BitNum(int num, int i) {
return (num & (1 << (i - 1))) > 0 ? 1 : 0;
}
//从0 ~ 63先对第一行进行处理
void get_firstLine(int num) {
for (int i = 1; i <= 6; ++ i) {
ways[1][7 - i] = get_BitNum(num, i);
}
for (int i = 1; i <= 6; ++ i) {
if (ways[1][i] > 0) {
++ nows[1][i];
++ nows[1][i - 1];
++ nows[1][i + 1];
++ nows[2][i];
}
}
}
//根据第line - 1行的情况,决定第 line 行的位置是否开灯
void only_oneWay(int line) {
for (int i = 1; i <= 6; ++ i ){
if (nows[line - 1][i] % 2 == 1) {
ways[line][i] = 1;
++ nows[line - 1][i];
++ nows[line + 1][i];
++ nows[line][i - 1];
++ nows[line][i + 1];
++ nows[line][i];
}
}
}
//因为 1 ~ 4 行必定都全部关上了,直接判断第五行是否也都关上
bool judge() {
for (int i = 1; i <= 6; ++ i) {
if (nows[5][i] % 2 == 1) return false;
}
return true;
}
//输出关灯的方案
void printf_way(int k) {
pr("PUZZLE #%d\n", k);
for (int i = 1; i <= 5; ++ i) {
pr("%d", ways[i][1]);
for (int j = 2; j <= 6; ++ j) {
pr(" %d", ways[i][j]);
}
pr("\n");
}
}
//调试程序用的--用于输出某个数组的情况
void test(int arr[10][10]) {
pr("--------------------------\n");
for (int i = 1; i <= 5; ++ i) {
for (int j = 1; j <= 6; ++ j) {
pr("%d ", arr[i][j]);
}
pr("\n");
}
}
//对nows数组重置
void copy_light_to_nows() {
for (int i = 1; i <= 5; ++ i ) {
for (int j = 1; j <= 6; ++ j) {
nows[i][j] = light[i][j];
}
}
}
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int n;
rin;
for (int k = 1; k <= n; ++ k) {
//读入灯的初始状态
for (int i = 1; i <= 5; ++ i) {
for (int j = 1; j <= 6; ++ j) {
sc("%d", &light[i][j]);
}
}
//第一行从 0 ~ 63 去分情况讨论
int length = (int)pow(2, 6) - 1;
for (int i = 0; i <= length; ++ i) {
//重置nows、ways数组
copy_light_to_nows();
MEM(ways, 0);
//分行处理
get_firstLine(i);
only_oneWay(2);
only_oneWay(3);
only_oneWay(4);
only_oneWay(5);
//判断该方案是否合理
if (judge()) {
printf_way(k);
break;
}
}
}
return 0;
}
2、POJ 3624 Charm Bracelet(01背包)
原题链接:http://poj.org/problem?id=3624
题目大意
类似01背包,一个容积为M的袋子,有N件珠宝,每一件珠宝重量为w [ i ],价值为 d [ i ],问在不超过容积的前提下,能得到的最大价值数。
思路
dp [ n ] [ m ] 表示在第 1 到第 n 件珠宝中挑选出重量不超过m的最大价值数。
则有:dp [ n ] [ m ] = max (dp [ n - 1] [ m ] , dp [ n - 1 ] [ m - w [ i ] ] + d [ i ])
(分:第 n 件不选 和 选第 n 件,所以对两者求max即可)
但是因为N * M 会超内存,根据状态转移方程,我们会发现,dp 数组每一项只和上一行有关系,所以开一个一维的滚动数组即可。
但需要注意,应当从 m 遍历到 1 ,不然会把第 n 行的状态赋给第 n 行。
//POJ 3624
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 3500, M = 13000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
int dp[M];
int w[N], d[N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int n, m;
sc("%d %d", &n, &m);
for (int i = 1; i <= n; ++ i) {
sc("%d %d", &w[i], &d[i]);
}
for (int i = 1; i <= n; ++ i) {
for (int j = m; j >= 1; -- j) {
if (j - w[i] >= 0)
dp[j] = max(dp[j], dp[j - w[i]] + d[i]);
}
}
pr("%d\n", dp[m]);
return 0;
}
3、POJ 1088 滑雪
原题链接:http://poj.org/problem?id=1088


思路
因为只能从高的滑向低的,那么最高的那个位置的最长长度只能是 1,也就是它自己。
而次高的,只能从最高的滑向它,而且还得是它们两个相邻的前提下,否则也只能是1。
进而我们可以推出,假如现在有一个高度 h,它的上下左右四个位置分别为 h1 > h、 h2 > h、 h3< h 、 h4 = h,那么很明显,只能由h1和h2滑向h,且为了最终滑行长度最长,h应该选择h1和h2中已经积累的长度中最长的。
而且还有一点就是,因为我们需要从高的位置遍历到低的位置,所以还需要对不同位置的高度进行排序,从高到低去动态规划。
//1088
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 10000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
struct height {
int num, x, y;
};
int dp[200][200]; //计算每个位置能达到的最长长度
int mapp[200][200]; //原先的高度
height hh[10010]; //存下每个高度及其坐标
bool cmp (height a, height b) {
return a.num > b.num;
}
int main() {
int r, c;
sc("%d %d", &r, &c);
int k = 0;
for (int i = 1; i <= r; ++ i) {
for (int j = 1; j <= c; ++ j) {
dp[i][j] = 1;
sc("%d", &mapp[i][j]);
hh[k].num = mapp[i][j];
hh[k].x = i;
hh[k].y = j;
++ k;
}
}
sort(hh, hh + k, cmp);
for (int i = 0; i < k; ++ i) {
int x = hh[i].x, y = hh[i].y;
if (mapp[x - 1][y] > mapp[x][y]) dp[x][y] = max(dp[x][y], dp[x - 1][y] + 1);
if (mapp[x + 1][y] > mapp[x][y]) dp[x][y] = max(dp[x][y], dp[x + 1][y] + 1);
if (mapp[x][y - 1] > mapp[x][y]) dp[x][y] = max(dp[x][y], dp[x][y - 1] + 1);
if (mapp[x][y + 1] > mapp[x][y]) dp[x][y] = max(dp[x][y], dp[x][y + 1] + 1);
}
int maxx = 0;
for (int i = 1; i <= r; ++ i) {
for (int j = 1; j <= c; ++ j) {
// pr("%d ", dp[i][j]);
maxx = max (maxx, dp[i][j]);
}
// pr("\n");
}
pr("%d\n", maxx);
return 0;
}
4、Leetcode 剑指 Offer 49. 丑数
题目
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明
1 是丑数。
n 不超过1690。
思路
设 dp [ n ] 为第 n + 1 个丑数,那么 dp [ n ] = min ( min ( dp [ a ] * 2, dp [ b ] * 3 ), dp [ c ] * 5 ),即当前的这个丑数,一定是由之前的某一个丑数得来的。
而无论哪一个丑数 * 2 / 3 / 5,最终也都能得到丑数,所以设置了a、b、c三个指针分别指向 2 、3 、5 当前走到哪个丑数,在计算当前的 dp[ n ] 的时候就取三个丑数 * 值以后的最小数,并且将指针后移。
class Solution {
public:
int dp[1700];
int nthUglyNumber(int n) {
dp[0] = 1;
int a = 0, b = 0, c = 0;
for (int i = 1; i < n; ++ i) {
dp[i] = min(min(dp[a] * 2, dp[b] * 3), dp[c] * 5);
if (dp[i] == dp[a] * 2) ++ a;
if (dp[i] == dp[b] * 3) ++ b;
if (dp[i] == dp[c] * 5) ++ c;
}
return dp[n - 1];
}
};
5、POJ 1661 Help Jimmy (往下跳)
原题链接:http://poj.org/problem?id=1661


思路
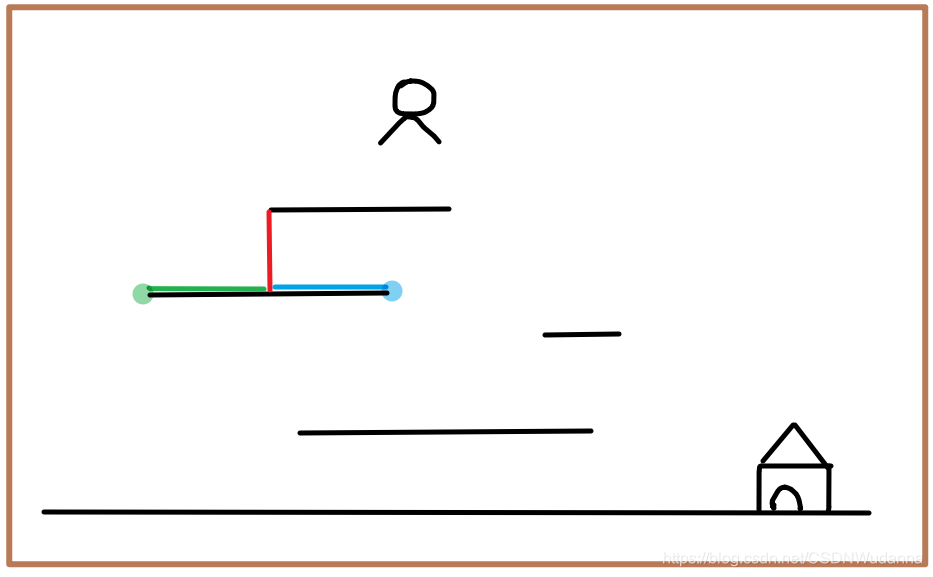
当老鼠掉到第一块板子上的时候,它有两种选择:向左走和向右走。
假如它向左走,那么在上图中, 从掉落到第一块板子的左端点到地面的最短距离 = 红色线段 + min(绿色线段 + 绿端点到地面的最短距离, 蓝色线段 + 蓝端点到地面的最短距离)。
进而从一块板子到地面的最短距离转移到另一块板子到地面的最短距离。
(因为速度是 1 米 / s,所以在数值上距离就是最终答案)
对于这道题,我们可以自定义一个结构体LR表示每一块板子的数据,l、r、h、min_l、min_r 分别表示板子的左端点横坐标、右端点横坐标、距离地面高度、左端点到地面的最短距离、右端点到地面的最短距离。
然后,这道题就可以通过这样的顺序求解:对每一块板子按高度 h 从低到高排序、从0到n - 1遍历板子求每块板的min_l和min_r、求小鼠最先掉落的板子、求最终最短路径。
//1661
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <sstream>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <vector>
#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <climits>
using namespace std;
#define ll long long
#define MEN(x, y) memset(x, y, sizeof x)
#define rin scanf("%d", &n)
#define rln scanf("%lld", &n)
#define rit scanf("%d", &t)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 1020;
const int MAXH = 30000;
//(val & 1) == 0偶, == 1奇。
#define getlength(array,len) {len = (sizeof(array) / sizeof(array[0]));}
struct LR {
int l, r, h;
int min_l, min_r;
};
LR arr[N];
bool cmp(LR & a, LR & b) {
return a.h < b.h;
}
int main() {
//freopen("D:\\in.txt", "r", stdin);
//freopen("D:\\out.txt", "w", stdout);
int t;
rit;
while (t --) {
int n, X, Y, Max;
sc("%d %d %d %d", &n, &X, &Y, &Max);
for (int i = 0; i < n; ++ i) {
sc("%d %d %d", &arr[i].l, &arr[i].r, &arr[i].h);
}
//按高度从低到高排序
sort(arr, arr + n, cmp);
//遍历板子得min_l和min_r
for (int i = 0; i < n; ++ i) {
//走左边
int flag = -10;
for (int j = i - 1; j >= 0; -- j) {
if (arr[j].l <= arr[i].l && arr[j].r >= arr[i].l) {
flag = j;
break;
}
}
//只能直接到地面
if (flag < 0) {
if (arr[i].h <= Max) arr[i].min_l = arr[i].h;
else arr[i].min_l = MAXH;
}
//有板子能跳
else {
if (arr[i].h - arr[flag].h <= Max) {
arr[i].min_l = min(arr[i].l - arr[flag].l + arr[flag].min_l,
arr[flag].r - arr[i].l + arr[flag].min_r)
+ arr[i].h - arr[flag].h;
}
else arr[i].min_l = MAXH;
}
//走右边
flag = -10;
for (int j = i - 1; j >= 0; -- j) {
if (arr[j].l <= arr[i].r && arr[i].r <= arr[j].r) {
flag = j;
break;
}
}
if (flag < 0) {
if (arr[i].h <= Max) arr[i].min_r = arr[i].h;
else arr[i].min_r = MAXH;
}
else {
if (arr[i].h - arr[flag].h <= Max) {
arr[i].min_r = min(arr[i].r - arr[flag].l + arr[flag].min_l,
arr[flag].r - arr[i].r + arr[flag].min_r) +
arr[i].h - arr[flag].h;
}
else arr[i].min_r = MAXH;
}
}
//从初始高处往下跳
int flag = -10;
for (int j = n - 1; j >= 0; -- j) {
if (arr[j].l <= X && X <= arr[j].r) {
flag = j;
break;
}
}
int ans;
if (flag < 0) ans = Y;
else {
ans = min(X - arr[flag].l + arr[flag].min_l,
arr[flag].r - X + arr[flag].min_r) + Y - arr[flag].h;
}
//debug
// for (int i = 0; i < n; ++ i) {
// pr("i == %d l == %d r == %d h == %d min_l == %d min_r == %d\n",
// i, arr[i].l, arr[i].r, arr[i].h, arr[i].min_l, arr[i].min_r );
// }
//输出
pr("%d\n", ans);
}
return 0;
}