DP 类型题二
- 【跳转DP 类型题一 (模型:数字三角形+最长上升子序列+背包】
- 一、状态机模型
- 1、AcWing 1057. 股票买卖 IV :两个状态转换
- 2、AcWing 1058. 股票买卖 V :三个状态转换
- 3、AcWing 1052. 设计密码 :T 维状态转换
- 二、状态压缩DP
- 1、AcWing 1064. 小国王 :九宫格限制
- 2、AcWing 292. 炮兵阵地 :十字限制
- 3、
- 三、区间DP
- 四、树形DP
- 五、数位DP
- 六、单调队列优化DP
- 七、斜率优化DP
【跳转DP 类型题一 (模型:数字三角形+最长上升子序列+背包】
!!!传送门~~~~~~~~~~~~~~~~
一、状态机模型
1、AcWing 1057. 股票买卖 IV :两个状态转换
原题链接:https://www.acwing.com/problem/content/description/1059/

/*
dp[i][j][0] 表示在前 i 天中,恰好使用 j 次交易机会,且目前没有持有股票的最大收益。
dp[i][j][1] 表示在前 i 天中,恰好使用 j 次交易机会,且目前持有股票的最大收益。
*/
#include<iostream>
#include<cstring>
using namespace std;
int dp[100010][110][2];
int main() {
int n, k;
cin >> n >> k;
//除了dp[i][0][0], 其他诸如dp[x][0][1]、dp[0][x][0/1]是不合法的
memset(dp, -0x3f, sizeof dp);
for (int i = 0; i <= n; ++ i) dp[i][0][0] = 0;
int ans = 0;
for (int i = 1; i <= n; ++ i) {
int a;
cin >> a;
for (int j = 1; j <= k; ++ j) {
// dp[i][j][0] = max(前一天也没有持股,前一天持股今天抛售);
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + a);
// dp[i][j][0] = max(前一天也持股,前一天没有持股今天买入);
dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - a);
//因为不一定要把k次机会全部用完,所以需要对过程取max
ans = max(ans, dp[i][j][0]);
}
}
cout << ans;
return 0;
}
2、AcWing 1058. 股票买卖 V :三个状态转换
原题链接:https://www.acwing.com/problem/content/1060/

【图解】
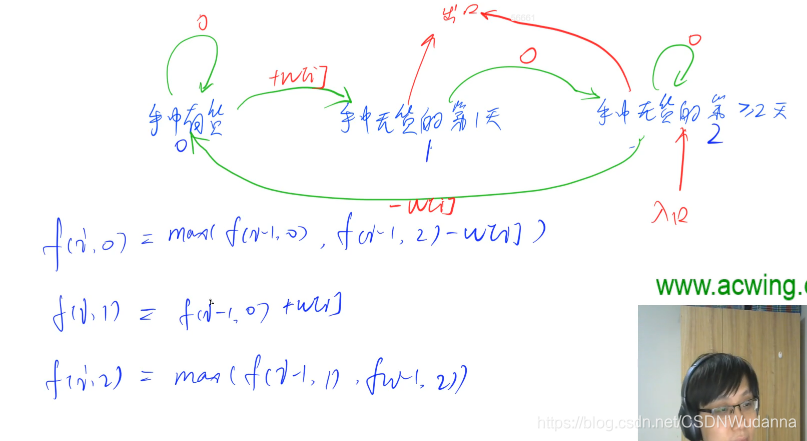
【代码】
#include<iostream>
#include<cstring>
using namespace std;
// dp[i][0] 表示前 i 天中,第 i 天持股的最大收益
// dp[i][1] 表示前 i 天中,第 i 天是冷却期的最大收益
// dp[i][2] 表示前 i 天中,第 i 天是非冷却期却没有持股的最大收益
int dp[100010][3];
int main() {
int n;
cin >> n;
dp[0][0] = dp[0][1] = -0x3f3f3f3f;
for (int i = 1; i <= n; ++ i) {
int a;
cin >> a;
// dp[i][0] = max(继续持股,第i天买入);
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - a);
// dp[i][1] = 第 i 天卖出
dp[i][1] = dp[i - 1][0] + a;
// dp[i][0] = max(前一天不是冷却期不持股保持今天不持股,前一天是冷却期保持今天不持股,);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1]);
}
cout << max(dp[n][1], dp[n][2]);
return 0;
}
3、AcWing 1052. 设计密码 :T 维状态转换
原题链接:https://www.acwing.com/problem/content/description/1054/


#include<iostream>
#include<cstring>
using namespace std;
const int N = 60;
const int modd = 1e9 + 7;
// dp[i][j] 表示密码后 i 个字符和子串 t 前 j 个字符相等的最大方案数
// 此时第 i + 1 位若与 j + 1 位相等,那么明显 dp[i + 1][j + 1] += dp[i][j];
// 若不相等,则按照kmp匹配那样找到能将两个字符对齐的 j
//其中dp[i][j] 中,若 i < j 是不合法的,但不必特判
//例如dp[2][5],一定有dp[2][5] = dp[0][3] = 0。
int dp[N][N], ne[N];
char s[N];
int main() {
int n;
cin >> n >> s + 1;
int m = strlen(s + 1);
for (int i = 2, j = 0; i <= m; ++ i) {
while (j && s[i] != s[j + 1]) j = ne[j];
if (s[i] == s[j + 1]) ++ j;
ne[i] = j;
}
dp[0][0] = 1;
//密码已经配备了前i个字母
for (int i = 0; i < n; ++ i) {
//密码前i个字母中长度为j的后缀 == 子串t中长度为j的前缀
for (int j = 0; j < m; ++ j) {
//此时密码要配对的下一位字母是k
for (int k = 'a'; k <= 'z'; ++ k) {
int jj = j; //因为看漏了这一步 卡了一周才明白……
while (jj && k != s[jj + 1]) jj = ne[jj];
if (k == s[jj + 1]) ++ jj;
if (jj < m) dp[i + 1][jj] = (dp[i + 1][jj] + dp[i][j]) % modd;
}
}
}
long long ans = 0;
for (int i = 0; i < m; ++ i) ans = (ans + dp[n][i]) % modd;
cout << ans << endl;
return 0;
}
二、状态压缩DP
1、AcWing 1064. 小国王 :九宫格限制
原题链接:https://www.acwing.com/problem/content/description/1066/
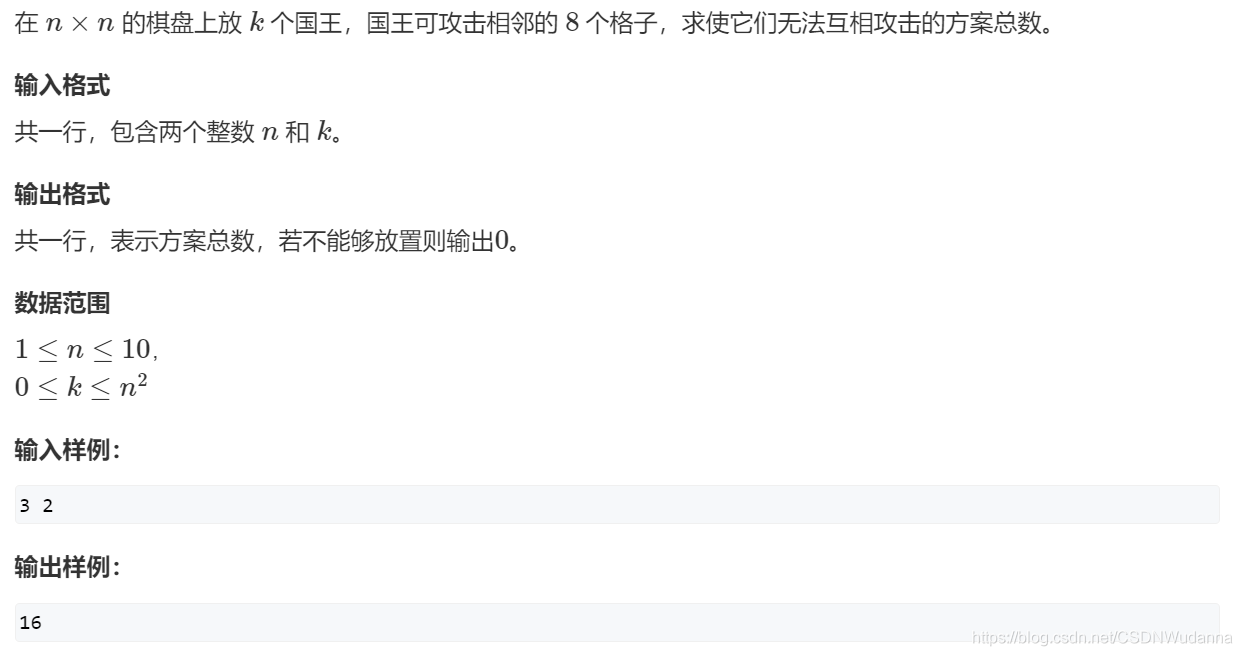
思路
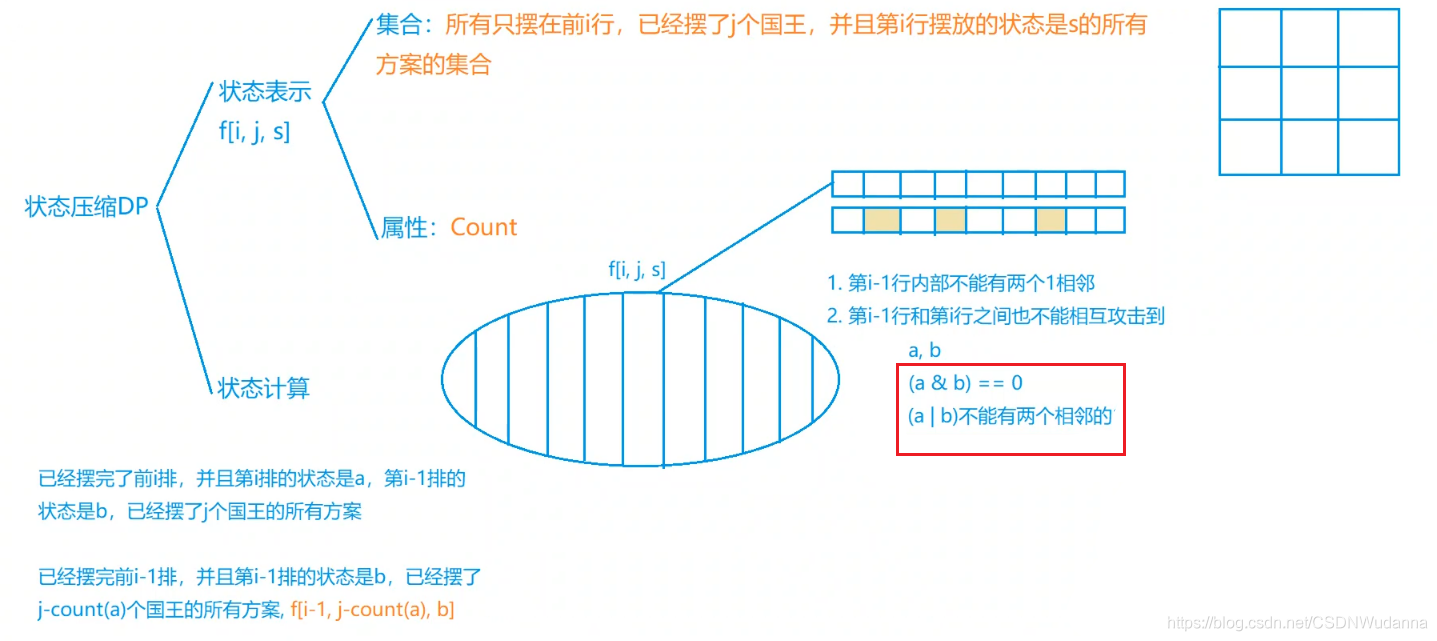
代码
#include<iostream>
#include<vector>
using namespace std;
const int N = 15, M = 110;
//dp[i][j][u] 表示前 i 行中一共安排了 j 个国王,同时最后一行的摆放方式是二进制的state[u](1-有国王,0-无国王)
long long dp[N][M][300];
//state存下所有不存在相邻1的数
//cnt[i] = state[i]二进制中 1 的个数
vector<int> state, cnt;
int n, m;
//判断a是否合法:存在相邻的1 - false
bool check(int a) {
for (int i = 0; i < n; ++ i) {
if ((a >> i) & 1 && (a >> (i + 1)) & 1)
return false;
}
return true;
}
//计算 a 的二进制中有多少个 1
int count(int a) {
int ans = 0;
for (int i = 0; i < n; ++ i) {
if ((a >> i) & 1) ++ ans;
}
return ans;
}
int main() {
cin >> n >> m;
//预处理
for (int i = 0; i < 1 << n; ++ i) {
if (check(i)) {
state.push_back(i);
cnt.push_back(count(i));
}
}
//初始化
dp[0][0][0] = 1;
//前 i 行棋盘(多处理1行方便后面输出答案)
for (int i = 1; i <= n + 1; ++ i) {
// 前 i 行棋盘一共用了多少个国王
for (int j = 0; j <= m; ++ j) {
// 第 i - 1 行国王摆放情况
for (int k = 0; k < state.size(); ++ k) {
// 第 i 行国王摆放情况
for (int u = 0; u < state.size(); ++ u) {
int a = state[k], b = state[u];
// 数量合法
if (cnt[u] <= j) {
// if ( a[i]和b[i]不同时为1 && a[i]和b[i-1]、b[i+1]不同时为1 )
if (!(a & b) && check(a | b)) {
dp[i][j][u] += dp[i - 1][j - cnt[u]][k];
}
}
}
}
}
}
cout << dp[n + 1][m][0];
return 0;
}
2、AcWing 292. 炮兵阵地 :十字限制
原题链接:https://www.acwing.com/problem/content/description/294/

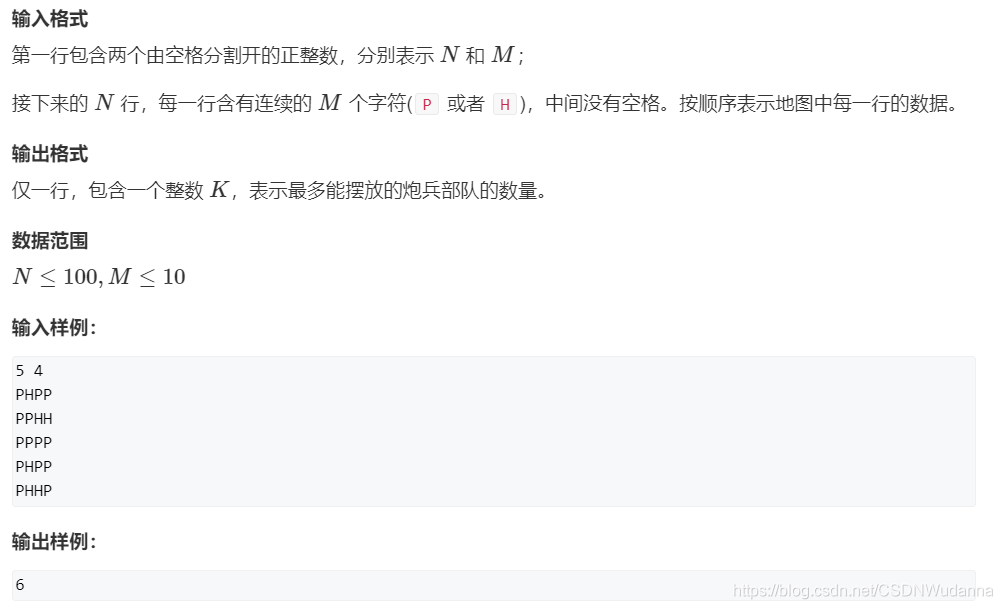
// 这道题主要是一开始只用了两维去表示,dp[i][j]表示处理前 i 行且最后一行状态时state[j].
// 但很明显在状态转移时,dp[i - 1][k] 和 dp[i - 2][u] 即便j、k、u这三行是合法的,
// 但是对于 dp[i - 1][k] 所表示方案中的第 i - 3 行不一定不会和 dp[i - 2][u] 中的第 i - 3 行矛盾。
// 所以需要再增加一维,使得状态转移时所表示的方案是一一对应的。
#include<iostream>
#include<vector>
using namespace std;
const int N = 110, M = 70;
// dp[i][j][k]表示处理前 i 行,第i - 1行状态是state[j]、第 i 行状态是state[k]
int dp[2][M][M];
vector<int> state, cnt;
int book[N]; //二进制表示地图,1 - H,0 - P
int n, m;
//判断状态是否合法:两个1之间距离小于2 - false
bool check(int a) {
for (int i = 0; i < m; ++ i) {
if (((a >> i) & 1) && (((a >> (i + 1)) & 1) || ((a >> (i + 2)) & 1))) return false;
}
return true;
}
//计算a中有多少个1
int count(int a) {
int res = 0;
for (int i = 0; i < m; ++ i) {
if ((a >> i) & 1) ++ res;
}
return res;
}
int main() {
cin >> n >> m;
char c;
//预处理地图
for (int i = 1; i <= n; ++ i) {
for (int j = m - 1; j >= 0; -- j) {
cin >> c;
if (c == 'H') book[i] += 1 << j;
}
}
//预处理出在水平方向上合法的状态
for (int i = 0; i < 1 << m; ++ i) {
if (check(i)) {
state.push_back(i);
cnt.push_back(count(i));
}
}
//处理前 i 行
for (int i = 1; i <= n + 2; ++ i) {
// 第 i - 2 行的状态
for (int j = 0; j < state.size(); ++ j) {
// 第 i - 1 行的状态
for (int k = 0; k < state.size(); ++ k) {
//第 i 行的状态
for (int u = 0; u < state.size(); ++ u) {
int a = state[j], b = state[k], c = state[u];
// 垂直方向有两个1及以上:continue
if ((c & b) || (c & a) || (b & a)) continue;
// 方案和地图有矛盾:continue
if ((c & book[i]) || (b & book[i - 1])) continue;
// 因为 i 是奇偶交替,所以直接 & 1 可以有滚动数组的效果
dp[i & 1][k][u] = max(dp[i & 1][k][u], dp[i - 1 & 1][j][k] + cnt[u]);
}
}
}
}
cout << dp[n + 2 & 1][0][0]; //需要加2,因为dp[n+1][0][0]中,第n行不一定要是state[0]
return 0;
}