1.问题

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。
返回 nums 构建的最大二叉树。

示例 1

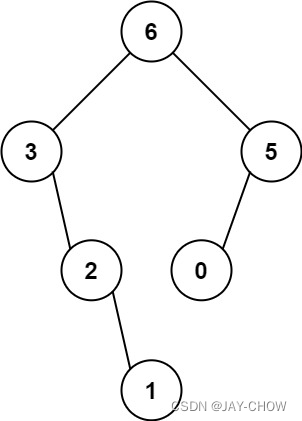
在这里插入图片描述

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1] 解释：递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
[3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
空数组，无子节点。
[2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
空数组，无子节点。
只有一个元素，所以子节点是一个值为 1 的节点。

[0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
只有一个元素，所以子节点是一个值为 0 的节点。
空数组，无子节点。

示例 2

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数互不相同

2.解题思路

2.1 递归

确定最大值位置，假定为 index
构造节点root，则root.left可以递归构造，范围为[start, index-1]
root.right递归构造，范围为[index+1, end]
终止条件 start>end

详见代码。

2.2 单调栈

以 [3,2,1,6,0,5] 为例：

构造节点 3，入栈；
构造节点 2，它比栈顶元素 3 小，所以，它是 3 的右子节点，直接入栈；
构造节点 1，它比栈顶元素 2 小，所以，它是 2 的右子节点，直接入栈；
构造节点 6，它比栈顶元素 1 大，所以，1 是它的左子节点，弹出 1；同样地，栈- 顶元素 2 也比它小，弹出 2 并做为它的左子节点；把栈顶所有比它小的元素都弹出，最后弹出的是 3，所以，最终是 3 做为 6 的左子节点，并把 6 入栈；
构造节点 0，它比栈顶元素 6 小，所以，它是 6 的右子节点，直接入栈；
构造节点 5，它比栈顶元素 0 大，所以，0 是它的左子节点，弹出 0；接着比较，它比栈顶元素 6 小，所以，它是 6 的右子节点，入栈；
最后，栈中元素为 [6,5]，栈底元素为 6，是最终的根节点；

动态图最直观，可参见B站大神录制的视频。

3.代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //递归构造
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length-1);
    }

    private TreeNode build(int[] nums, int start, int end){
        if(end<start){
            return null;
        }
        //1.找到最大值
        int max=Integer.MIN_VALUE;
        //最大值索引
        int index=start;
        for(int i=start;i<=end;i++){
            if(max<nums[i]){
                max=nums[i];
                index=i;
            }
        }
        //2.构造节点
        TreeNode root=new TreeNode(max);
        //3.左子树
        root.left=build(nums, start, index-1);
        //4.右子树
        root.right=build(nums, index+1, end);
        return root;
    }

    //单调栈
    public TreeNode constructMaximumBinaryTree2(int[] nums) {
        //单调栈
        Deque<TreeNode> stack=new ArrayDeque<>();
        //遍历
        for(int num: nums){
            //构造节点
            TreeNode root=new TreeNode(num);
            //比较当前栈顶元素，若大于num，则其为栈顶元素的右节点；
            //否则，遍历到栈底，将栈底节点置为root的左节点
            while(!stack.isEmpty() && num>stack.peek().val){
                root.left=stack.pop();
            }
            //比栈顶元素小的情况
            if(!stack.isEmpty()){
                stack.peek().right=root;
            }
            //入栈
            stack.push(root);
        }
        return stack.peekLast();
    }
}