参考博客：
1 解析图示最清楚
动态卷积之CondConv思想和代码实现_&永恒的星河&的博客-CSDN博客
2 知乎的解释，简洁明了
CondConv代码解析 - 知乎
知乎提供code：External-Attention-pytorch/CondConv.py at master · xmu-xiaoma666/External-Attention-pytorch · GitHub
2 中知乎的评论给出的更好的代码
CondConv-pytorch/condconv.py at master · nibuiro/CondConv-pytorch · GitHub

论文题目: CondConv: Conditionally Parameterized Convolutions for Efficient Inference

论文地址:  https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1904.04971

代码地址:  https://link.zhihu.com/?target=https%3A//github.com/tensorflow/tpu/tree/master/models/official/efficientnet/condconv

1 介绍

Cond conv： 是2019年发表在Google Brains上关于卷积CondConv的文章
即插即用的模块

常规卷积进行构建网络,有如下假设:所有的样本共享卷积网络中的卷积参数.
需求：
提升模型容量就需要增加网络的参数,深度,通道数,这将导致模型的计算量和参数量增加,模型部署难度大。若要模型的实时性高,这就需要模型拥有较低的参数量和计算量.
 

cond conv目的：提升模型的容量，同时保持实时性。
cond conv核心思想：为了打破传统卷积的特性,CondConv将卷积核参数化为多个专家知识的线性组合
公式： (a1*W1+a2*W2+...+an*Wn)*x
a1,a2,a3,...an是通过梯度下降法学习的权重系数
x是输入样本.可以通过提升专家的数量来提升模型的容量,这比提升卷积核的尺寸更有效,同时专家知识只需要一次线性组合,就可以提升模型容量的同时保持高效的推理.

Mixture of Experts（MoE）公式：α1*(W1∗x)+. . .+αn(Wn∗x)
Mixture of Experts（MoE）结构： 采用更细粒度的集成方式，每一个卷积层都拥有多套权重，卷积层的输入分别经过不同的权重卷积之后组合输出,缺点是但这计算量依旧很大.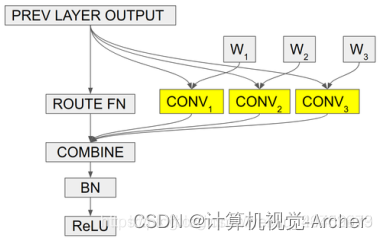


CondConv公式: (α1*W 1+ . . . + αn*Wn)∗x       =α1*(W1∗x)+. . .+αn(Wn∗x) 与MoE等同
Cond conv结构：可以解决MoE计算大问题，降低计算量。
既然输入相同，卷积是一种线性计算，COMBINE也是一个线性计算（比如加权求和）,作者将多套权重加权组合之后，只做一次卷积就能完成相当的效果！
2者区别： MoE是每个卷积核分别与x计算再组合，cond conv是先组合卷积核，在与x计算。

细致实现流程图（感谢这位博主的绘制，参考博客1）(tensorflow version)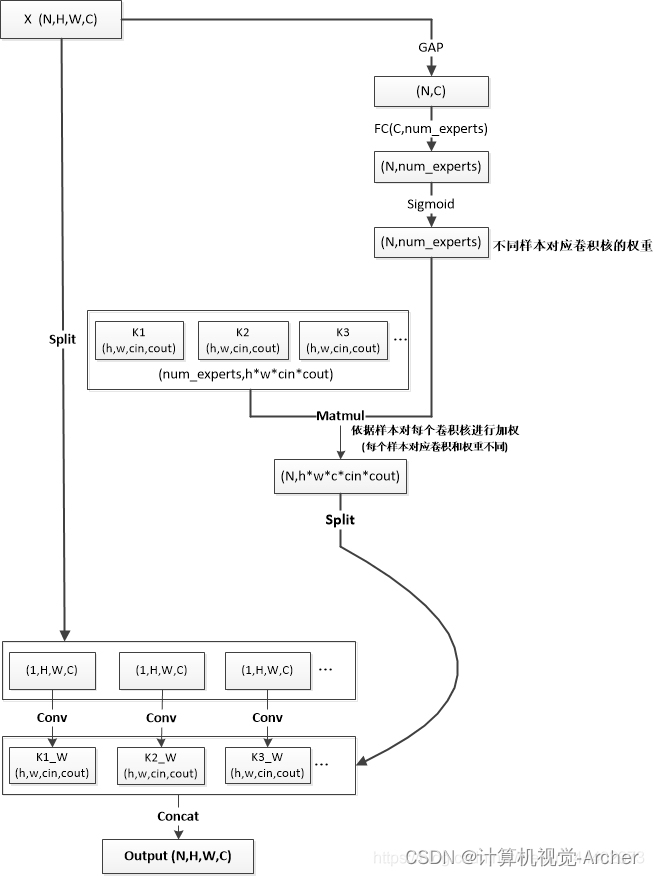

输入：X(N,H,W,C)
N：数据Batch的大小
H和W：输入图片的高和宽
C：输入图片的通道数
两条输出：右边输出，左边输出,最后对各自的输出进行整合.
(h,w,cin,cout)表示卷积核大小
h和w分别表示卷积核的高和宽
cin,cout分别表示卷积核的输入和输出通道数.

右边线路:由计算样本生成多个卷积核的各自权重
step1: 对输入X，进行GAP操作(GlobalAveragePooling2D)操作,具体在维度(H,W),
输出大小为(N,C)
step2: 之后经过FC层,学习不同输入样本对用num_experts个卷积的各自的权重系数,输出为(N,num_experts)
step3: 采用Sigmoid归一化到(0,1)之间,输出为(N,num_experts)
step4: 将step3输出权重系数和num_experts个卷积核权重通过矩阵的相乘,赋予到相应的卷积上,输出各个样本对应加权后的卷积核权重,输出大小为:(N,h*w*cin*cout)
step5: 将step4中的输出在N维度进行Split操作,得到各个样本对应加权后卷积核

左边线路:对输入X依次通过对应加权输出的卷积核权重,完成CondConv。
step1:将X在N维度进行split操作
step2:将step1中输出结果和右边线输出对应卷积权重进行卷积操作,之后进行Concat。

上面已经说的很细致了，下面介绍实验效果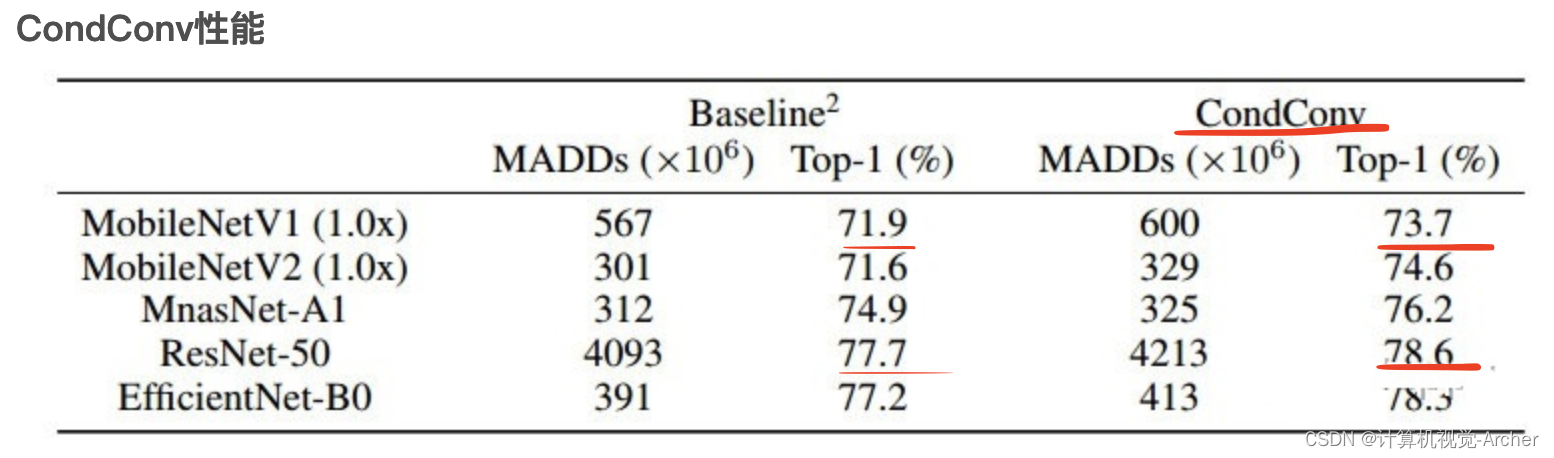


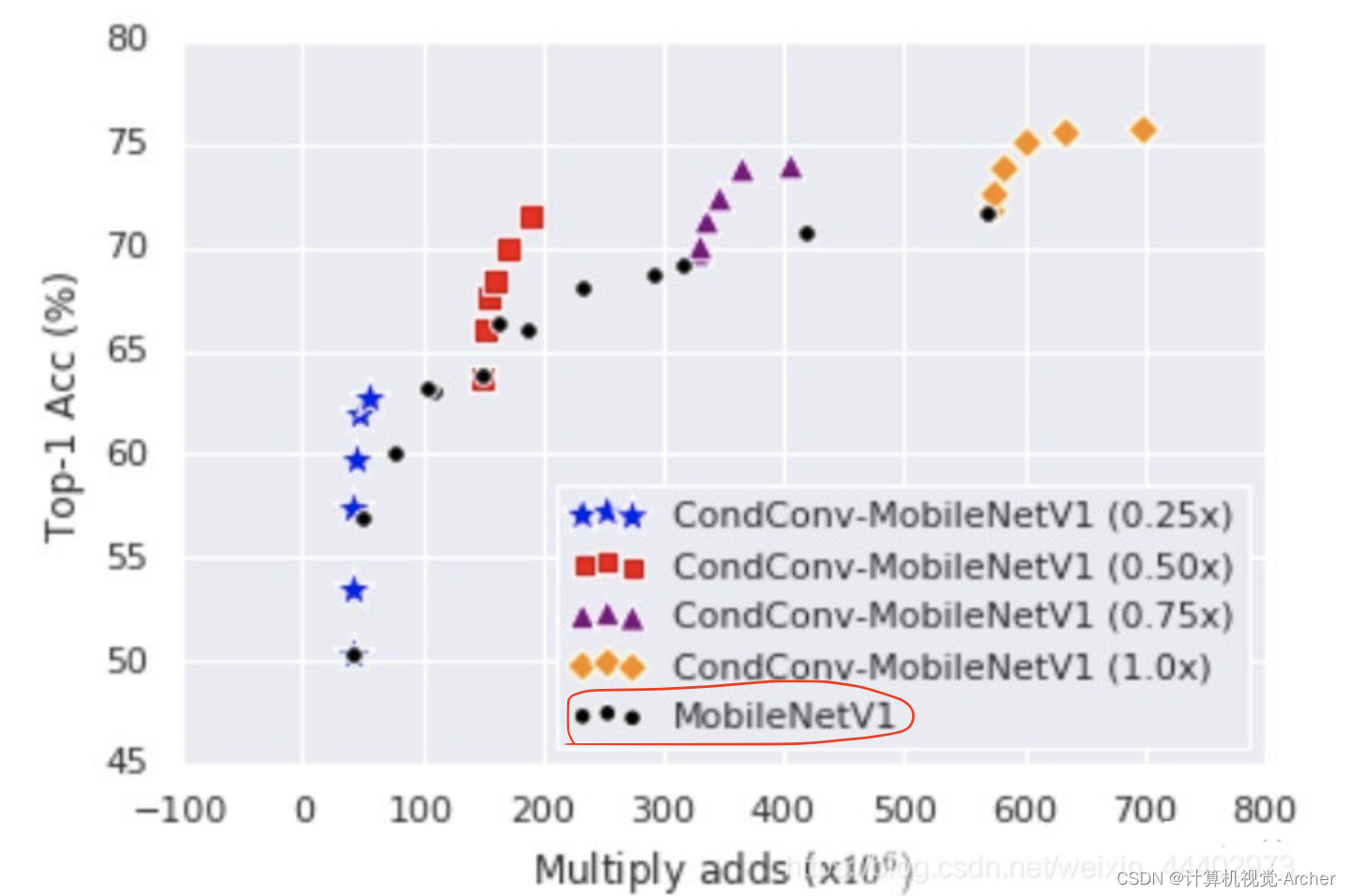
总结：
CondConv打破了静态卷积的假设：卷积核对所有输入“一视同仁”。
提升模型容量并保持高效推理：提升卷积核生成函数的尺寸与复杂度。
由于卷积核参数仅需计算一次，相比卷积计算，这些额外的计算量可以忽略。
即：提升卷积核生成的计算量>(优于)添加更多卷积或更多通道数。

2 代码详解torch(来自知乎条件参数化卷积（CondConv）)

为了方便理解 ，下面把原代码中的 initial_weights 和 bias 相关的部分删掉了。
rount_fn部分：是 attention 函数，输入为 [N, C, H, W]
需要两个参数，in_planes为输特征通道数，K为专家个数。
输出shape为[N, K]，即这里是针对N个批次的K个卷积核的权重。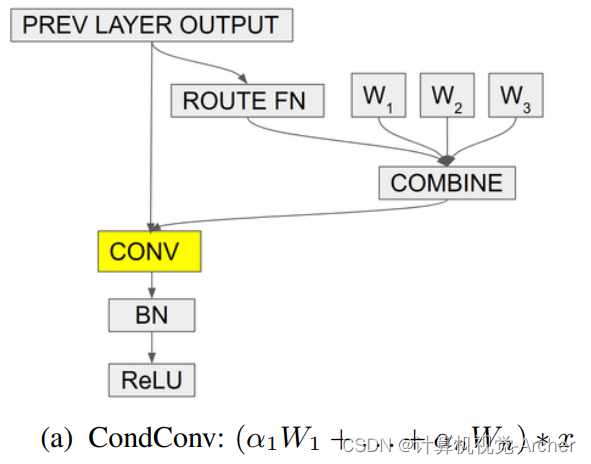

# 输入为 [N, C, H, W]，需要两个参数，Cin为输入特征通道数，K 为专家个数
class Attention(nn.Module):
    def __init__(self,Cin,K):
        super().__init__()
        self.avgpool=nn.AdaptiveAvgPool2d(1)  # 池化操作
        self.net=nn.Conv2d(Cin, K, kernel_size=1)  # Cin通道变为K
        self.sigmoid=nn.Sigmoid()  # 归一化

    def forward(self,x):
        # 将输入特征全局池化为 [N,Cin,H,W]->[N, Cin, 1, 1]
        att=self.avgpool(x)
        # 使用1*1卷积，转化为 [N, Cin, 1, 1]->[N, K, 1, 1]
        att=self.net(att)
        # 将特征转化为二维 [N, K, 1, 1]->[N, K]
        att=att.view(x.shape[0],-1) 
        # 使用 sigmoid 函数输出归一化到 [0,1] 区间
        return self.sigmoid(att)

CondConv 是一种特殊的动态卷积，增加卷积核生成函数的大小和复杂性（增加capacity容量）
CondConv还利用样本的特点来提高模型性能（权重是基于样本生成的类似SE block）
 

class CondConv(nn.Module):
    def __init__(self,Cin,Cout,kernel_size,stride,padding=0,
                 groups=1,K=4):
        super().__init__()
        self.Cin = Cin  # 输入通道
        self.Cout = Cout  # 输出通道
        self.K = K  # K个权重
        self.groups = groups
        self.kernel_size = kernel_size
        self.stride = stride
        self.padding = padding
        self.attention = Attention(Cin=Cin,K=K)
        # weight [K, Cout, Cin, kernelz_size, kernel_size]
        self.weight = nn.Parameter(torch.randn(K,Cout,Cin//groups,
                                             kernel_size,kernel_size),requires_grad=True)

    def forward(self,x):
        ### part1 weight
        # 调用 attention 函数得到归一化的权重 [N,Cin,H,W]->[N, K]
        N,Cins, H, W = x.shape
        softmax_att=self.attention(x)
        
        ### part2 x
        # [N, Cin, H, W]->[1, N*Cin, H, W]
        x=x.view(1, -1, H, W)
        
        ### part3 conv
        # 生成随机weight[K, Cout, C_in/groups, 3, 3] (卷积核一般为3*3)
        # 注意添加了 requires_grad=True，这样里面的参数是可以优化的
        weight = self.weight
        # 改变 weight 形状为 [K,Cout,Cin,3,3]->[K, C_out*(C_in/groups)*3*3]
        weight = weight.view(self.K, -1) 

        # part4: 新的wconv = weight*conv
        # 矩阵相乘：[N, K]*[K, Cout*(Cin/groups)*3*3] = [N, Cout*(Cin/groups)*3*3]
        aggregate_weight = torch.mm(softmax_att,weight)
        # 改变形状为：[N, Cout*Cin/groups*3*3]->[N*Cout, Cin/groups, 3, 3]，即新的卷积核权重
        aggregate_weight = aggregate_weight.view(
            N*self.Cout, self.Cin//self.groups,
            self.kernel_size, self.kernel_size)
        # 用新生成的卷积核进行卷积，[1, N*Cin, H, W] conv [N*Cout, Cin/groups, 3, 3]
        # 输出为 [1, N*Cout, H, W]
        output=F.conv2d(x,weight=aggregate_weight,
                        stride=self.stride, padding=self.padding,
                        groups=self.groups*N)
        # 形状恢复为 [N, C_out, H, W]        
        output=output.view(N, self.out_planes, H, W)
        return output