目录
什么是哈夫曼树
哈夫曼树的定义
哈夫曼树的构造
图解操作
代码实现
代码解析
哈夫曼树的特点
哈夫曼编码
不等长编码
二叉树用于编码
哈夫曼编码实例
什么是哈夫曼树
我们先举个例子:
要将百分制的考试成绩转化成五分制的成绩
if(score < 60)
grade = 1;
else if(score < 70)
grade = 2;
else if(score < 80)
grade = 3;
else if(score < 90)
grade = 4;
else
grade = 5;这种情况其实是一棵判定树:
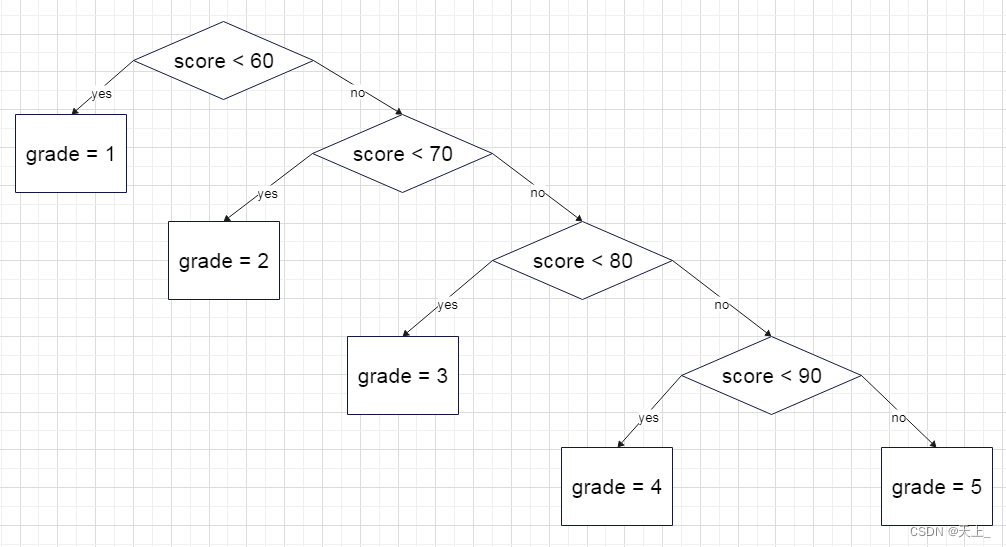
这种方式要看各成绩段的学生分布,如果60以下的同学比较多,那么判断的次数就会很少;但是如果90多的同学比较多的情况下,那么要判断4次的情况就会很多,整体的判断效率不高。
我们考虑学生成绩分布的概率:
| 分数段 | 0-59 | 60-69 | 70-79 | 80-89 | 90-100 |
|---|---|---|---|---|---|
| 比例 | 0.05 | 0.15 | 0.40 | 0.30 | 0.10 |
那么判断效率就为:
现在我们想要让判断的效率更高一点,修改一下判定树:
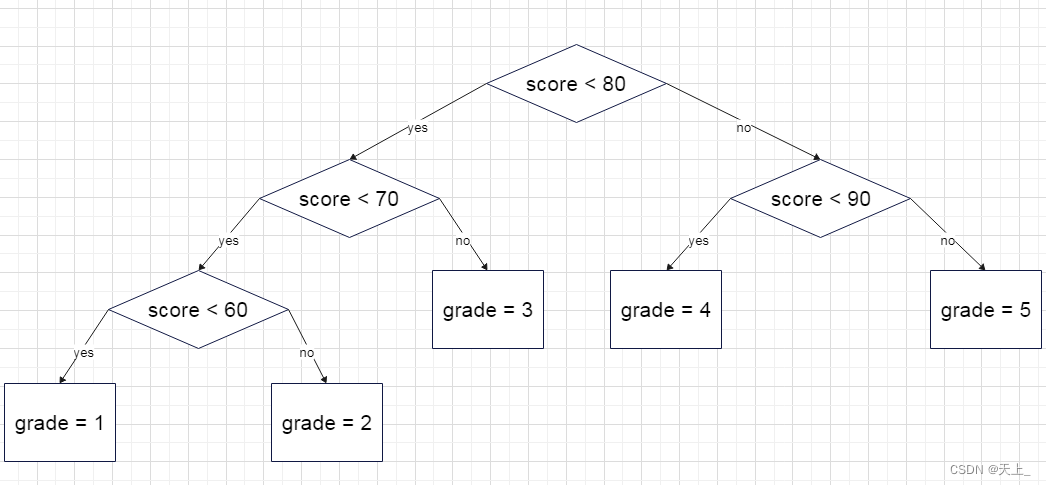
这样的判断效率就为:
写成代码就为:
if(score < 80)
{
if(score < 70)
{
if(score < 60)
{
grade = 1;
}
else
{
grade = 2;
}
}
else
{
grade = 3;
}
}
else if(score < 90)
{
grade = 4;
}
else
{
grade = 5;
}如何根据结点不同的查找频率构造更有效的搜索树?
就涉及到了我们要讲的哈夫曼树
哈夫曼树的定义
带权路径长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值
,从根结点到每个叶子结点的长度为
,则每个叶子结点的带权路径长度之和就为:
最优二叉树或哈夫曼树:WPL最小的二叉树。
例:有五个叶子结点,它们的权值为{1,2,3,4,5},用此权值序列可以构造出形状不同的多个二叉树。
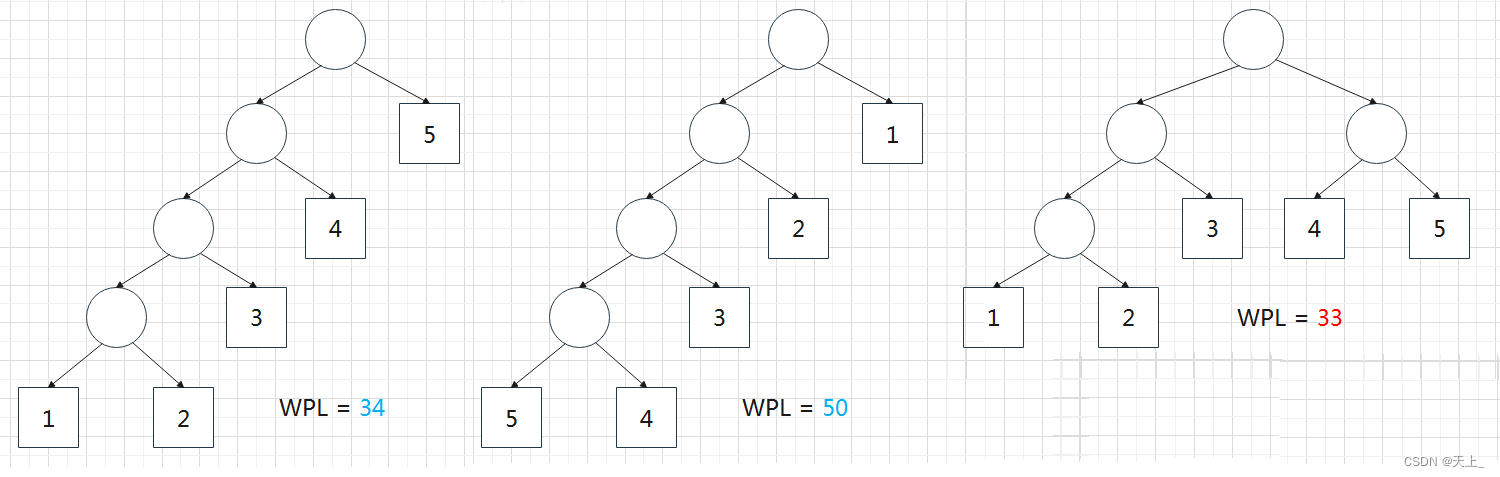
哈夫曼树的构造
给出一个权值序列,构造出一棵哈夫曼树。
例:{1,2,3,4,5}
每次把权值最小的两棵二叉树合并,具体:
图解操作
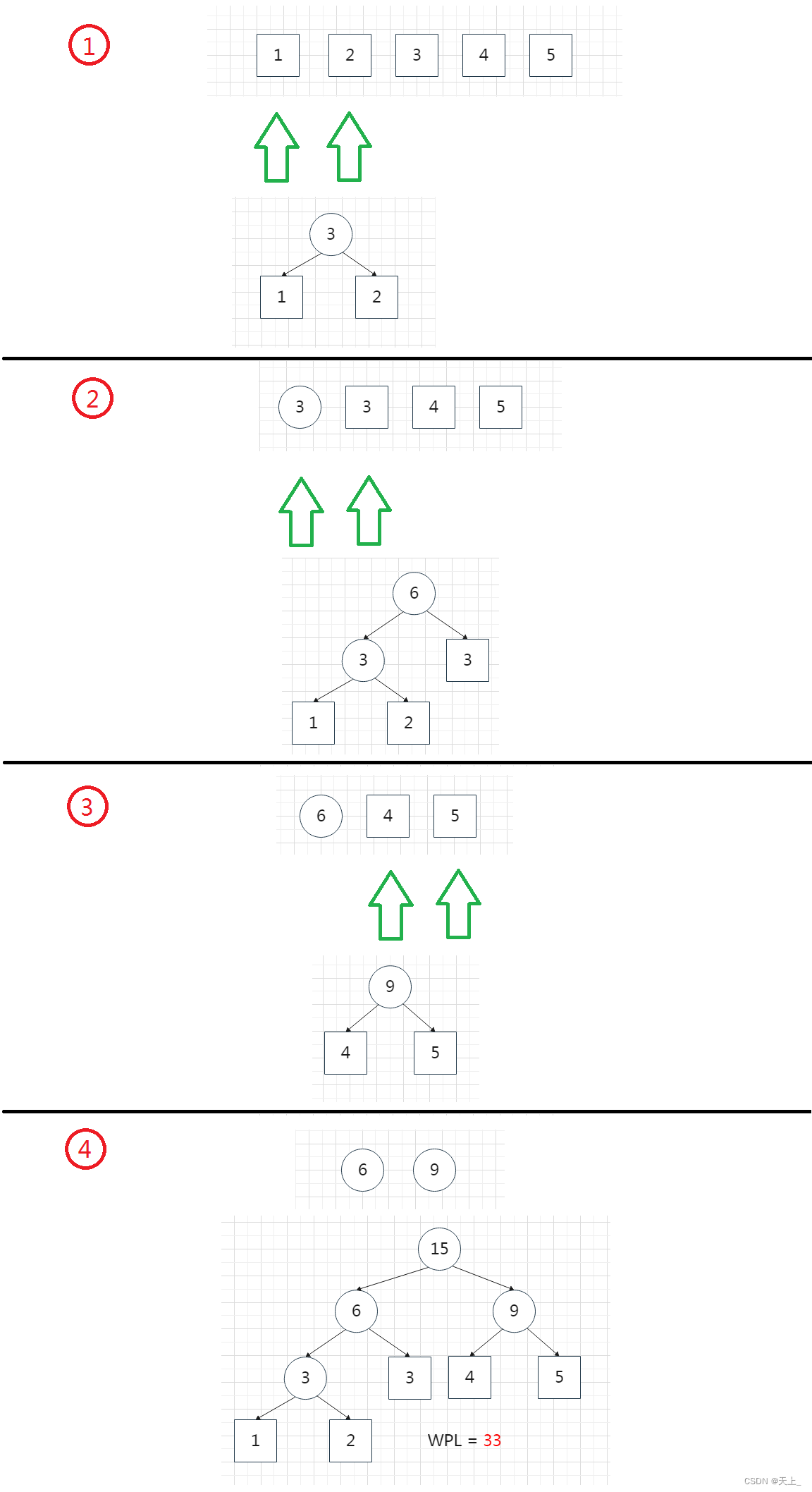
哈夫曼树的构造是比较简单的,要找出两个最小值,就可以运用我们前面学过的最小堆来找了,这比从小到大排好序的效率会更高。下面我们来看一下代码的实现。
代码实现
typedef struct TreeNode *HuffmanTree;
struct TreeNode
{
int Weight;
HuffmanTree Left,Right;
}
HuffmanTree Huffman(MinHeap H)
{ /*假设H->Size个权值已经存在H->Elements[]->Weight里*/
int i;
HuffmanTree T;
BuildMinHeap(H);/*将H->Elements[]按权值调整为最小堆*/
for (i=1;i<H->Size;i++)
{
/*做H->Size-1次合并*/
T=malloc( sizeof( struct TreeNode));/*建立新结点*/
T->Left=DeleteMin(H);
/*从最小堆中删除一个结点,作为新T的左子结点*/
T->Riqht=DeleteMin(H);
/*从最小堆中删除一个结点,作为新T的右子结点*/
T->Weight=T->Left->Weiqht + T->Right->Weight;
/*计算新权值*/
Insert(H,T);/*将新T插入最小堆*/
}
T=DeleteMin(H);
return T;
}代码解析

这段代码定义了一个结构体类型TreeNode和一个指向TreeNode类型的指针HuffmanTree。TreeNode结构体包含三个成员变量:Weight表示权值,Left表示左子树指针,Right表示右子树指针。
HuffmanTree指针类型可以指向TreeNode类型的对象,用于表示哈夫曼树的结点。
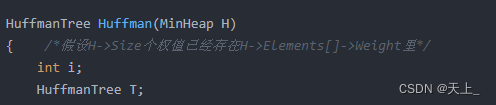
函数的输入参数是一个最小堆H,其中存储了每个字符出现的频率。
变量 i 的作用是用于循环合并最小堆中的结点,每次循环合并两个权值最小的结点,直到只剩下一个根结点。
T的作用是用于创建新的Huffman树结点,每次合并两个最小权值的结点时,都会创建一个新的结点T,并将两个最小权值结点作为T的左右子结点,然后将T插入到最小堆中。
最终,最小堆中只剩下一个根结点,即为Huffman树的根结点,返回该结点即可。
![]()
函数首先调用BuildMinHeap函数将H中的元素按照权值调整为最小堆。
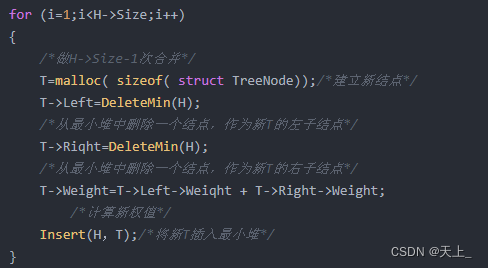
然后进入for循环,将最小堆中的所有结点合并成一棵哈夫曼树:
首先,建立一个新的结点T,作为合并后的新结点。
然后,从最小堆中删除两个权值最小的结点,分别作为新结点T的左子结点和右子结点。
接着,计算新结点T的权值,即左子结点和右子结点的权值之和。
最后,将新结点T插入最小堆中。
这个过程会重复执行H->Size-1次,因为最终的哈夫曼树只有一个根结点,所以需要将所有结点合并成一个。
![]()
最后,从最小堆中删除最后一个结点,即哈夫曼树的根结点,
并返回该结点作为哈夫曼树的根。
哈夫曼树构造完成。整体的时间复杂度为
哈夫曼树的特点
- 没有度为1的结点
哈夫曼树是一棵最优二叉树,每个叶子结点都对应着一个字符,
而每个非叶子结点都是两个子结点的父结点,表示两个字符的合并。
如果存在度为1的结点,那么这个结点只有一个子结点,就不能表示两个字符的合并,因此不符合哈夫曼树的定义。
- n个叶子结点的哈夫曼树共有2n-1个结点
我们最开始学二叉树时,在其中提到了二叉树的几个重要性质。
“对任何非空二叉树T,若n0表示叶节点的个数,n2是度为2的非叶节点个数,那么两者满足关系n0 = n2 +1。”
因为哈夫曼树没有度为1的结点,叶结点为n个,那么度为2的非叶结点个数就为n-1个;
故而总结点数就等于n + (n - 1) = 2n - 1。
- 哈夫曼树的任意非叶结点的左右子树交换之后仍是哈夫曼树
交换哈夫曼树中任意非叶结点的左右子树时,它的深度和权值并没有发生改变,因此仍然满足哈夫曼树的定义。
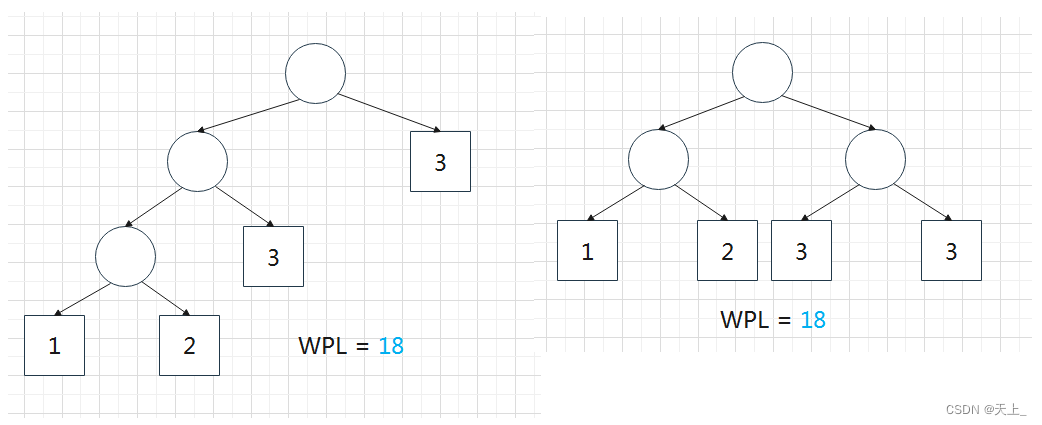
- 对同一组权值{
},存在不同构的两棵哈夫曼树
对一组权值{1,2,3,3},不同构的两棵哈夫曼树:
哈夫曼编码
不等长编码
抛出问题:给定一段字符串,如何对字符进行编码,可以使得该字符串的编码存储空间最少?
【例】假设有一段文本,包含58个字符,并由以下7个字符构成:a,e,i,s,t,空格(sp),换行(nl);这7个字符出现的次数不同。如何对这7个字符进行编码,使得总编码空间最少?
【分析】
(1)用等长ASCII编码(ASCII占1个字节,8个比特位):58 * 8 = 464位;
(2)用等长3位编码(因为只有7个字符,3位的编码足够表达8个对象):58 * 3 = 174位;
(3)不等长编码:出现频率高的字符用的编码短些,出现频率低的字符则可以编码长些
怎么进行不等长编码呢?
我们不妨假设:
a:0
e:0
s:10
t:11
......
那么在这样的不等长编码下,1011是什么字符串的编码?
a e a a:1 0 1 1
a e t:1 0 1 1
s t:1 0 1 1
这样就出现了同一个编码,却译出不同的几个字符串了,即存在二义性。
要避免二义性,就要满足一个条件:前缀码
前缀码prefix code:任何字符的编码都不是另一字符编码的前缀
例如,s的前缀为1,而1就可以理解为a,这就不符合前缀码的条件了。
二叉树用于编码
为了保证我们的编码不出现二义性,我们可以用二叉树来编码。
用二叉树编码:
(1)左分支:0
(2)右分支:1
(3)字符只在叶结点上
【例】现有四个字符的频率:a:4,u:1,x:2,z:1。
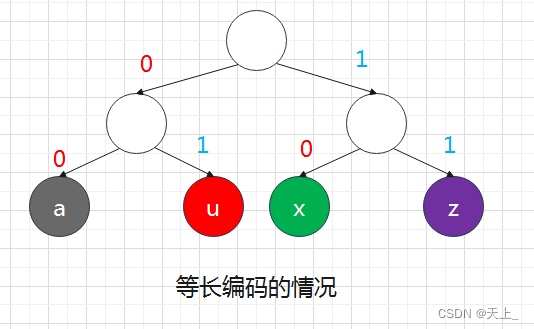
前面说过的前缀码,是当字符出现在叶结点时;如果字符出现在非叶结点上,就说明它不满足前缀码的条件:

所以这就是为什么用二叉树来编码时,字符只在叶结点上。
接下来的问题是,怎么样构造才能使得付出的代价最小?
看到刚才举的例子:
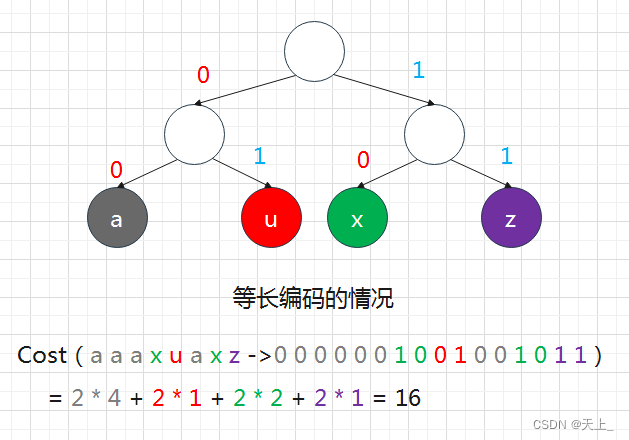
这就和我们讲哈夫曼树时是差不多的情况,我们根据频率来把二叉树重构一下:
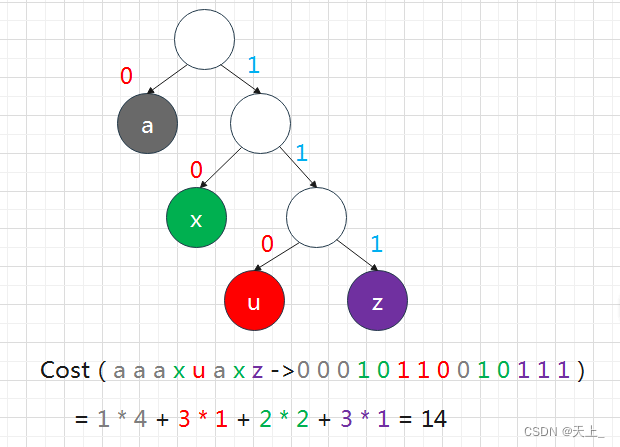
这样不存在二义性,代价也最小。
哈夫曼编码实例
【例】
| a | e | i | s | t | sp | nl | |
| 10 | 15 | 12 | 3 | 4 | 13 | 1 |
用上面学过的构造哈夫曼树的方法,每次选取最小的两个值构造二叉树,整个过程如下
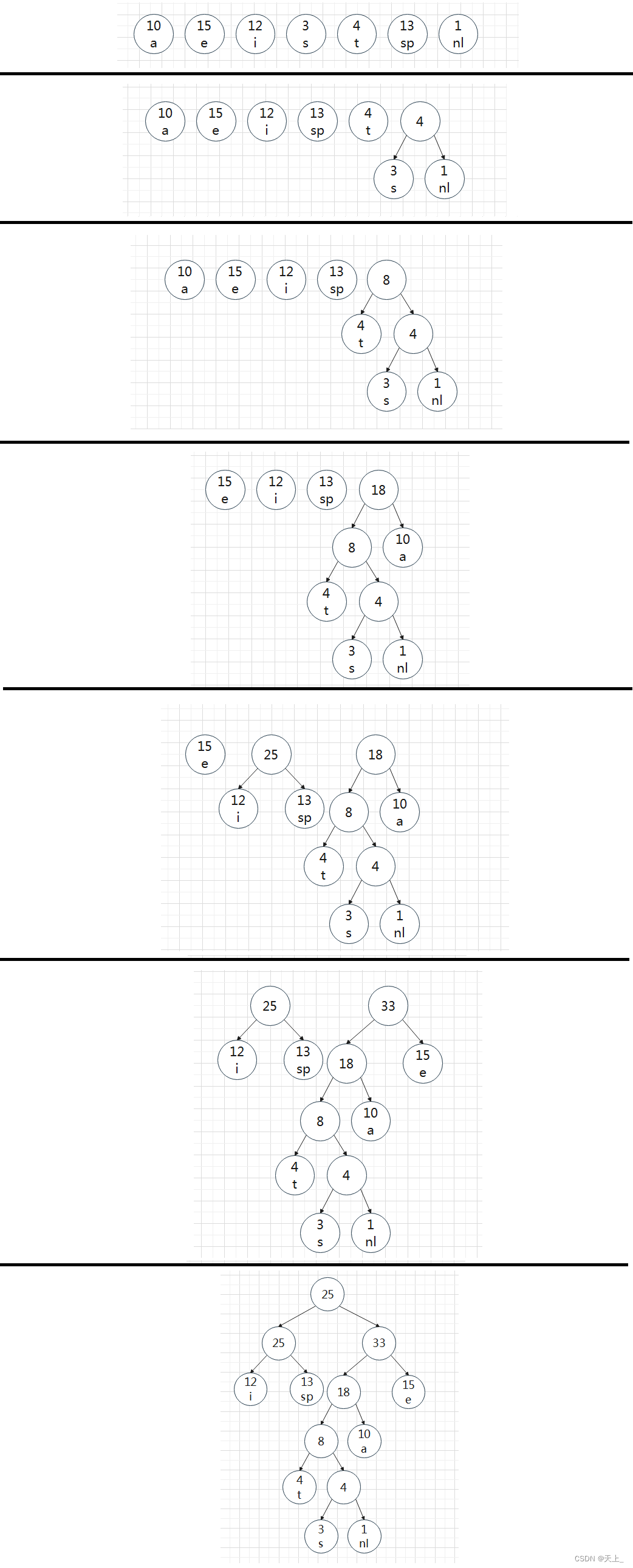
最终构造出来的哈夫曼编码树:
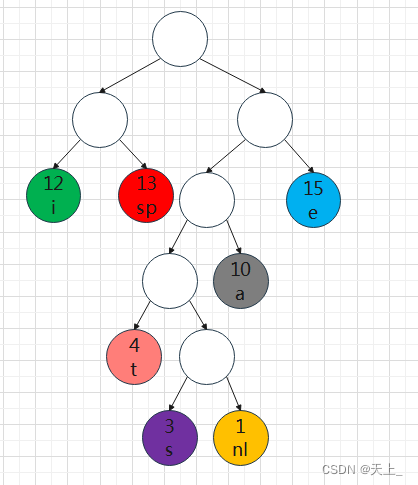
end
学习自:MOOC数据结构——陈越、何钦铭