前端：20 个常见的前端算法题

现在面试中，算法出现的频率越来越高了，大厂基本必考

今天给大家带来 20 个常见的前端算法题，重要的地方已添加注释，如有不正确的地方，欢迎多多指正 💕

1、两数之和

题目：给定一个数组 nums 和一个目标值 target，在该数组中找出和为目标值的两个数

输入： nums: [8, 2, 6, 5, 4, 1, 3] ； target:7

输出： [2, 5]

// 时间复杂度O(n)、 空间复杂度O(n)
function twoNumAdd(arr, target) {
  if (Array.isArray(arr)) {
    // 使用map将遍历过的数字存起来，空间换时间
    let map = {};
    for (let i = 0; i < arr.length; i++) {
      // 从map中查找是否有key 等于 target-nums[i]，如果有，则条件成立，返回结果
      if (map[target - arr[i]] !== undefined) {
        return [target - arr[i], arr[i]];
      } else {
        // 条件不成立，将该值存起来
        map[arr[i]] = i;
      }
    }
  }
  return [];
}

2、三数之和

题目：给定一个数组 nums，判断 nums 中是否存在三个元素a，b，c，使得 a + b + c = target，找出所有满足条件且不重复的三元组合

输入： nums: [5, 2, 1, 1, 3, 4, 6] ；target:8

输出： [[1, 1, 6], [1, 2, 5], [1, 3, 4]]

// 用`双端指针`的方式，将三数之和转化为两数之和
function findThree(arr, target) {
  // 先将数组从小到大排序
  arr.sort();
  let result = [];
  for (let i = 0; i < arr.length; i++) {
    // 跳过重复的arr[i]值, 比如[2, 1, 1],跳过第二个1
    if (i && arr[i] === arr[i - 1]) continue;
    let left = i + 1;
    let right = arr.length - 1;

    // 双端指针left、right
    while (left < right) {
      let sum = arr[i] + arr[left] + arr[right];
      if (sum > target) {
        right--;
      } else if (sum < target) {
        left++;
      } else {
        // 先取arr[left]，然后left++, 两步合成一步；arr[right--]同样的逻辑
        result.push([arr[i], arr[left++], arr[right--]]);
        while (arr[left] === arr[left - 1]) {
          // 跳过重复的arr[left]值,
          left++;
        }
        while (arr[right] === arr[right + 1]) {
          // 跳过重复的arr[right]值
          right--;
        }
      }
    }
  }
  return result;
}

3、版本号排序

题目：输入一组版本号，输出从大到小的排序

输入： [‘2.1.2’, ‘0.402.1’, ‘3.20.1’, ‘0.1.8’, ‘5.1.2’, ‘1.3.4.5’]

输出： [‘5.1.2’, ‘3.20.1’, ‘2.1.2’, ‘1.3.4.5’, ‘0.402.1’, ‘0.1.8’]

function versionSort(arr) {
  return arr.sort((a, b) => {
    let i = 0;
    const arr1 = a.split(".");
    const arr2 = b.split(".");
    while (true) {
      // 取出相同位置的数字
      const s1 = arr1[i];
      const s2 = arr2[i];
      i++;
      // 若s1 或 s2 不存在，说明相同的位置已比较完成，接下来比较arr1 与 arr2的长度，长的版本号大
      if (s1 === undefined || s2 === undefined) {
        return arr2.length - arr1.length;
      }
      if (s1 === s2) continue;
      // 比较相同位置的数字大小
      return s2 - s1;
    }
  });
}

4、第一个不重复的字符

题目：输入一个字符串，找到第一个不重复字符的下标

输入： ‘abcabcde’

输出： 6

// 时间复杂度O(n)、 空间复杂度O(n)
function findOneStr(str) {
  if (!str) return -1;
  // 使用map存储每个字符出现的次数
  let map = {};
  let arr = str.split("");
  arr.forEach(item => {
    let val = map[item];
    // val为undefined时，表示未存储，map[item] = 1；否则map[item] = val + 1
    map[item] = val ? val + 1 : 1;
  });
  // 再遍历一遍找到出现1次的下标
  for (let i = 0; i < arr.length; i++) {
    if (map[arr[i]] == 1) {
      return i;
    }
  }
  return -1;
}

5、字符串所有排列组合

题目：输入一个字符串，打印出该字符串中，所有字符的排列组合

输入： ‘abc’

输出： [‘abc’, ‘acb’, ‘bca’, ‘bac’, ‘cab’, ‘cba’]

/**
 * 利用回溯算法，计算所有字符串的组合
 * @param {array} list - 字符串列表
 * @param {array} result - 最终的结果
 * @param {string} current - 当前的字符串
 * @param {string} temp - 当前固定的字符
*/
function stringGroup(list = [], result = [], current = "", temp = "") {
  current += temp;
  if (list.length === 0) {
    // 递归的出口，将对应结果添加到list中
    return result.push(current);
  }
  for (let i = 0; i < list.length; i++) {
    // 每次递归 固定第一个字符
    temp = list.shift();
    stringGroup(list, result, current, temp);
    // 将删除的temp重新添加到queue尾部，实现将数组反转的效果，如[a,b,c]反转为[c,b,a]
    list.push(temp);
  }
  // 这里去重是解决str中有重复的字母，比如str为'aacd'
  return [...new Set(result)];
}

6、冒泡排序

时间复杂度为O(n²)，稳定排序算法

function bubbleSort(arr) {
  let length = arr.length;
  // 外层循环用控制 排序进行多少轮
  for (let i = 0; i < length; i++) {
    // 内层循环用于每一轮的数据比较
    // 注意j的长度范围 length - i - 1
    for (let j = 0; j < length - i - 1; j++) {
      // 相邻元素，大的放到后面
      if (arr[j] > arr[j + 1]) {
        // 交换位置
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

7、选择排序

时间复杂度为O(n²)，不稳定

function selectSort(arr) {
  // 定义index存储最小值的下标
  let index;
  // 外层循环用控制 排序进行多少轮
  for (let i = 0; i < arr.length - 1; i++) {
    index = i;
    // 内层循环用于每一轮的数据比较
    // 注意j的起始范围是 i + 1
    for (let j = i + 1; j < arr.length; j++) {
      // 寻找最小值
      if (arr[j] < arr[index]) {
        // 保存最小值的下标
        index = j;
      }
    }
    // 如果 index 不是目前的头部元素，则交换两者
    if (index !== i) {
      [arr[i], arr[index]] = [arr[index], arr[i]];
    }
  }
  return arr;
}

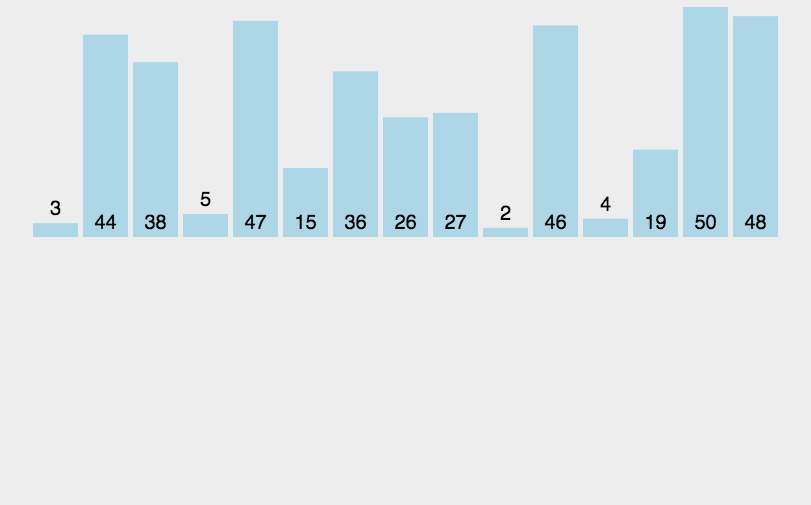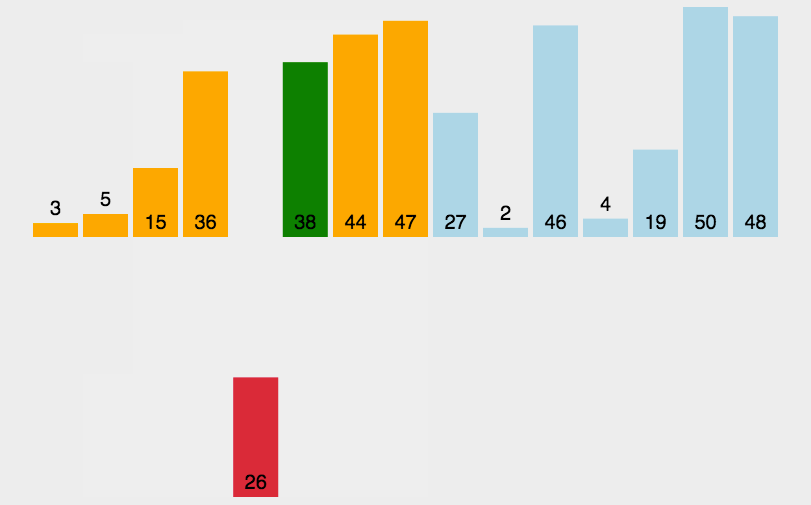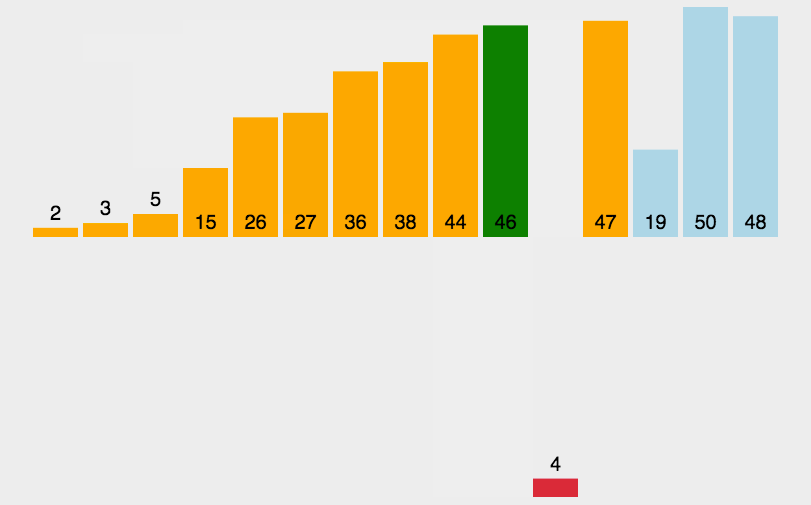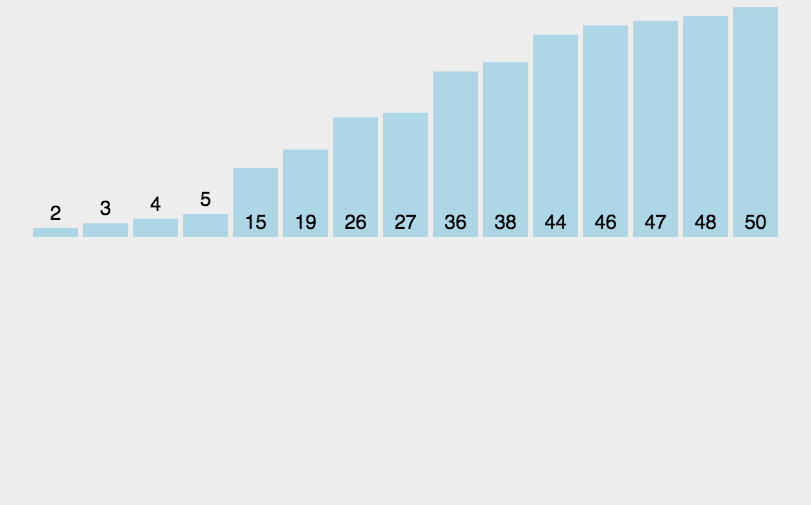
8、插入排序

时间复杂度为O(n²)，稳定

function insertSort(arr) {
  // 从第 2 个元素开始遍历序列
  for (let i = 1; i < arr.length; i++) {
    let j = i;
    //记录要插入的目标元素
    let target = arr[j];
    //从 target 所在位置向前遍历，直至找到一个比目标元素小的元素，目标元素插入到该元素之后的位置
    while (j > 0 && arr[j - 1] > target) {
      //移动前一个元素的位置，将其向后移动一个位置
      arr[j] = arr[j - 1];
      j--;
    }
    arr[j] = target;
  }
  return arr;
}

9、快速排序

时间复杂度为O(nlogn)，不稳定

function quickSort(list) {
  // 当list.length <= 1时，退出递归
  if (list.length <= 1) return list;
  // 找到中间节点
  let mid = Math.floor(list.length / 2);
  // 以中间节点为基准点，比该节点大的值放到right数组中，否则放到left数组中
  let base = list.splice(mid, 1)[0];
  let left = [];
  let right = [];
  list.forEach(item => {
    if (item > base) {
      right.push(item);
    } else {
      left.push(item);
    }
  });
  // 重新组合数组
  return quickSort(left).concat(base, quickSort(right));
}

10、归并排序

时间复杂度为O(nlogn)，稳定

function MergeSort(array) {
  let len = array.length;

  // 当每个子序列中仅有1个元素时返回
  if (len <= 1) {
    return array;
  }
  // 将给定的列表分为两半
  let num = Math.floor(len / 2);
  let left = MergeSort(array.slice(0, num));
  let right = MergeSort(array.slice(num, array.length));
  return merge(left, right);

  function merge(left, right) {
    let [l, r] = [0, 0];
    let result = [];
    // 从 left 和 right 区域中各个取出第一个元素，比较它们的大小
    while (l < left.length && r < right.length) {
      // 将较小的元素添加到result中，然后从较小元素所在的区域内取出下一个元素，继续进行比较；
      if (left[l] < right[r]) {
        result.push(left[l]);
        l++;
      } else {
        result.push(right[r]);
        r++;
      }
    }
    // 如果 left 或者 right 有一方为空，则直接将另一方的所有元素依次添加到result中
    result = result.concat(left.slice(l, left.length));
    result = result.concat(right.slice(r, right.length));
    return result;
  }
}

11、列表转成树

题目：输入一组列表如下，转化成树形结构

输入：

[
  { id: 1, title: "child1", parentId: 0 },
  { id: 2, title: "child2", parentId: 0 },
  { id: 3, title: "child1_1", parentId: 1 },
  { id: 4, title: "child1_2", parentId: 1 },
  { id: 5, title: "child2_1", parentId: 2 }
]

输出：

tree=[
  {
    "id": 1,
    "title": "child1",
    "parentId": 0,
    "children": [
      {
        "id": 3,
        "title": "child1_1",
        "parentId": 1
      },
      {
        "id": 4,
        "title": "child1_2",
        "parentId": 1
      }
    ]
  },
  {
    "id": 2,
    "title": "child2",
    "parentId": 0,
    "children": [
      {
        "id": 5,
        "title": "child2_1",
        "parentId": 2
      }
    ]
  }
]

function listToTree(data) {
  // 使用对象重新存储数据, 空间换时间
  let map = {};
  // treeData存储最后结果
  let treeData = [];
  // 遍历原始数据data，存到map中，id为key，值为数据
  for (let i = 0; i < data.length; i++) {
    map[data[i].id] = data[i];
  }
  // 遍历对象
  for (let i in map) {
    // 根据 parentId 找到的是父节点
    if (map[i].parentId) {
      if (!map[map[i].parentId].children) {
        map[map[i].parentId].children = [];
      }
      // 将子节点放到父节点的 children中
      map[map[i].parentId].children.push(map[i]);
    } else {
      // parentId 找不到对应值，说明是根结点，直接插到根数组中
      treeData.push(map[i]);
    }
  }
  return treeData;
}

12、深度优先遍历

题目：对树进行遍历，从第一个节点开始，遍历其子节点，直到它的所有子节点都被遍历完毕，然后再遍历它的兄弟节点

输入：上文第 11 题生成的 tree

输出： [1, 3, 4, 2, 5]

// 递归版本
function deepTree(tree, arr = []) {
  if (!tree || !tree.length) return arr;
  tree.forEach(data => {
    arr.push(data.id);
    // 遍历子树
    data.children && deepTree(data.children, arr);
  });
  return arr;
}

// 非递归版本
function deepTree(tree) {
  if (!tree || !tree.length) return;
  let arr = [];
  let stack = [];
  //先将第一层节点放入栈
  for (let i = 0, len = tree.length; i < len; i++) {
    stack.push(tree[i]);
  }
  let node;
  while (stack.length) {
    // 获取当前第一个节点
    node = stack.shift();
    arr.push(node.id);
    //如果该节点有子节点，继续添加进入栈顶
    if (node.children && node.children.length) {
      stack = node.children.concat(stack);
    }
  }
  return arr;
}

13、广度优先遍历

题目：以横向的维度对树进行遍历，从第一个节点开始，依次遍历其所有的兄弟节点，再遍历第一个节点的子节点，一层层向下遍历

输入：上文第 11 题生成的 tree

输出： [1, 2, 3, 4, 5]

function rangeTree(tree) {
  if (!tree || !tree.length) return;
  let arr = [];
  let node, list = [...tree];
  // 取出当前节点
  while ((node = list.shift())) {
    arr.push(node.id);
    node.children && list.push(...node.children);
  }
  return arr;
}

14、树形结构查找节点

题目：查找树形结构中符合要求的节点

输入：
tree：上文第 11 题生成的 tree
func： data => data.title === “child2_1”

输出：{ id: 5, parentId: 2, title: “child2_1” }

/**
* 查找节点
* @param {array} tree - 树
* @param {function} func - 查找条件
* */
function findTreeNode(tree, func) {
  for (const data of tree) {
    // 条件成立 直接返回
    if (func(data)) return data;
    if (data.children) {
      const res = findTreeNode(data.children, func);
      // 结果存在再返回
      if (res) return res;
    }
  }
  return null;
}
// 测试
findTreeNode(tree, data => data.title === "child2_1")

15、二叉查找树

题目：判断一个数组，是否为某二叉查找树的前序遍历结果，二叉查找树特点是所有的左节点比父节点的值小，所有的右节点比父节点的值大

输入： [5, 3, 2, 1, 4, 6, 7, 8, 9]

输出： true

function preOrderOfBST(list) {
  if (list && list.length > 0) {
    // 前序遍历，第一个值为根节点
    var root = list[0];
    // 找到数组中，第一个比根节点大的节点，即为右子树的节点
    for (var i = 0; i < list.length; i++) {
      if (list[i] > root) {
        break;
      }
    }
    // 遍历右子树的节点，要求所有右子树的节点都比根节点大
    for (let j = i; j < list.length; j++) {
      if (list[j] < root) {
        return false;
      }
    }
    var left = true;
    // 同理，递归判断左子树是否符合二叉查找树的规则
    if (i > 1) {
      left = preOrderOfBST(list.slice(1, i + 1));
    }
    var right = true;
    // 递归判断右子树是否符合二叉查找树的规则
    if (i < list.length) {
      right = preOrderOfBST(list.slice(i, list.length));
    }
    // 左、右子树都符合要求，则是一个二叉查找树
    return left && right;
  }
}

16、查找二叉树的路径

题目：查找二叉树和为某一值的路径

输入：二叉树结构如下，找到和为 11 的所有路径

输出： [[5, 3, 2, 1], [5, 6]]

/**
* 利用回溯算法，找到和为某一值的路径
* @param {object} node - 二叉树
* @param {number} num - 目标值
* @param {array} stack - 栈
* @param {number} sum - 当前路径的和
* @param {array} result - 存储所有的结果
* */
function findPath(node, num, stack = [], sum = 0, result = []) {
  stack.push(node.data);
  sum += node.data;

  // 找到所有的节点路径(包含叶子节点和子节点的所有情况之和)
  if (sum === num) {
    // if (!node.left && !node.right && sum === num) {  // 找到所有的叶子节点路径
    result.push(stack.slice());
  }
  if (node.left) {
    findPath(node.left, num, stack, sum, result);
  }
  if (node.right) {
    findPath(node.right, num, stack, sum, result);
  }
  // 回溯算法：不符合要求，退回来，换一条路再试
  // 叶子节点直接pop；子节点中的所有的节点递归完成后再pop
  stack.pop();
  return result;
}

17、买卖股票问题

题目：给定一个整数数组，其中第 i 个元素代表了第 i天的股票价格；
非负整数 fee 代表了交易股票的手续费用，求返回获得利润的最大值

输入： arr: [1, 12, 13, 9, 15, 8, 6, 16]； fee: 2

输出： 22

/**
 * 贪心算法求解
 * @param {array} list - 股票每天的价格列表
 * @param {number} fee - 手续费
 * */
function buyStock(list, fee) {
  // min为当前的最小值，即买入点
  let min = list[0],
    sum = 0;
  for (let i = 1; i < list.length; i++) {
    // 从1开始，依次判断
    if (list[i] < min) {
      // 寻找数组的最小值
      min = list[i];
    } else {
      // 计算如果当天卖出是否赚钱
      let temp = list[i] - min - fee;
      if (temp > 0) {
        // 赚钱 存数据
        sum += temp;
        // 关键代码：重新计算min，分两种情况，如果后面继续涨，则默认继续持有；若后面跌，则以后面的价格重新买入
        min = list[i] - fee;
      }
    }
  }
  return sum;
}

18、斐波那契数列

题目：从第 3 项开始，当前项等于前两项之和： 1 1 2 3 5 8 13 21 ……，计算第 n 项的值

输入： 10

输出： 89

// 使用动态规划，将复杂的问题拆分，也就是：`F(N) = F(N - 1) + F(N - 2)`，用数组将已经计算过的值存起来
function fib(n) {
  // 使用dp数组，将之前计算的结果存起来，防止栈溢出
  if (n < 2) return 1;
  let dp = [1, 1];
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
}

19、滑动窗口最大值

题目：给定一个数组 nums，有一个大小为 k 的滑动窗口，从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口中的 k 个数字。滑动窗口每次只向右移动一位，求返回滑动窗口最大值

输入： nums: [1,3,-1,-3,5,3,6,7]； k: 3

输出： [3, 3, 5, 5, 6, 7]

function maxSlidingWindow(nums, k) {
  // window存储当前窗口中数据的下标
  const window = [];
  // result存储窗口中的最大值
  const result = [];
  for (let i = 0; i < nums.length; i++) {
    if (i - window[0] > k - 1) {
      // 剔除窗口长度超出范围时左侧的最大值
      window.shift();
    }
    for (let j = window.length - 1; j >= 0; j--) {
      // 当前窗口的值依次和要插入的值做比较，如果小于要插入的值，剔除掉该值，直到window为空为止（保证window中最左侧的值为最大值）
      if (nums[window[j]] <= nums[i]) {
        window.pop();
      }
    }
    // 添加右侧新加入的值，插入新值时有两种情况：
    // 1、新值为最大值时，则window此时为空；
    // 2、新值不为最大值时，window已剔除掉比新值小的值
    window.push(i);
    if (i >= k - 1) {
      // 窗口是从0开始移动，当移动的距离大于等于目标范围后，以后再往后移动一次，就要写入当前窗口的最大值
      result.push(nums[window[0]]);
    }
  }
  return result;
}

20、最长递增子序列

题目：一个整数数组 nums，找到其中一组最长递增子序列的值

输入： [3,5,7,1,2,8]

输出： [3,5,7,8]

function lengthOfLIS(nums) {
  if (!nums.length) return 0;
  // 创建一个和原数组等长的数组dp，用来存储每一项的最长递增子序列
  // 比如[1,2,2] 表示第二项和第三项的最长递增子序列都为2
  let dp = new Array(nums.length).fill(1);
  // 双层for循环，每一项都和之前的所有项一一进行比较，计算出该项的最长递增子序列个数，存储到dp中
  for (let i = 0; i < nums.length; i++) {
    // 当前项依次和之前的每一项进行比较，累加出当前项的最长递增子序列
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[i]) {
        // 比较当前项已有的最大值和之前项最大值，比如当比较到第三项[1,2,2]时，如第三项比第二项大，所以第三项的计算结果为[1,2,3]
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
  }
  // 取出一组最长递增子序列的具体值（注意：最长递增子序列有可能有多组值，这里是只取出其中一组值）
  // 找到dp中的最大值，该值就是nums的最长递增子序列的个数
  let max = Math.max(...dp);
  let result = [];
  for (let i = max; i >= 1; i--) {
    // 倒序遍历，根据长度获取对应的值
    findArrNode(dp, i, result, nums);
  }
  return result;
}
function findArrNode(dp, value, result, arr) {
  // 找到符合条件最后一项的下标，这样才能保证数组的顺序是正确的
  let index = dp.lastIndexOf(value);
  // 存储对应的值
  result.unshift(arr[index]);
  // 对dp进行截取，保证只取最大项之前的数据
  dp.length = index + 1;
}