1. 基本概念
1.1 定义
-
聚类:发现数据中分组聚集的结构,根据数据中样本与样本之间的距离或相似度,依据类内样本距离小(相似度大)、类间样本距离大(相似度小)将样本划分为若干组/类/簇。
- 基于划分的聚类:无嵌套,将所有样本划分到互不重叠的子集(簇),且使得每个样本仅属于一个子集。
- 层次聚类:有嵌套,树形聚类结构,在不同层次对数据集进行划分,簇之间存在嵌套。
-
簇集合的其他区别
- 独占vs非独占:在非独占的簇中,样本点可以属于多个簇。
- 模糊vs非模糊:在模糊聚类中,一个样本点以一定的权重属于各个聚类簇。
- 部分vs完备:部分聚类只聚类部分数据。
- 异质vs同质:簇的大小、行政和密度是否有很大的差别。
-
簇的类型
- 明显分离的簇
- 基于中心的簇:簇内点和其“中心”较为相近,和其他簇的“中心”较远,球状簇。
- 基于邻近(连续)的簇:相比其他任何簇的点,每个点都至少和所属簇的某一个点更近。
- 基于密度的簇:簇是由高密度的区域形成的,簇之间是一些低密度区域。
- 基于概念的簇:同一个簇共享某种性质,整个性质是从整个集合推导出来的。
1.2 距离度量函数
距离度量函数应满足条件:
-
非负性: d i s t ( x i , y j ) ≥ 0 dist(x_i,y_j)\ge0 dist(xi,yj)≥0
-
不可分的同一性: d i s t ( x i , y j ) = 0 i f x i = x j dist(x_i,y_j)=0\quad if\quad x_i=x_j dist(xi,yj)=0ifxi=xj
-
对称性: d i s t ( x i , y j ) = d i s t ( x j , x i ) dist(x_i,y_j)=dist(x_j,x_i) dist(xi,yj)=dist(xj,xi)
-
三角不等式: d i s t ( x i , x j ) ≤ d i s t ( x i , x k ) + d i s t ( x k , x j ) dist(x_i,x_j)\le dist(x_i,x_k)+dist(x_k,x_j) dist(xi,xj)≤dist(xi,xk)+dist(xk,xj)
数据预处理:
- StandardScaler:对特征矩阵的列,将特征值取值范围标准化(0均值,1方差)
- MinMaxScaler:对特征矩阵的列,将特征值缩放到[0,1]区间
- Normalizer:对特征矩阵的行,将每个样本缩放到单位向量
距离函数:
-
闵可夫斯基距离: d i s t ( x i , x j ) = ( ∑ d = 1 D ∣ x i d − x j d ∣ p ) 1 p dist(x_i,x_j)=\big(\sum_{d=1}^D|x_{id}-x_{jd}|^p\big)^\frac{1}{p} dist(xi,xj)=(∑d=1D∣xid−xjd∣p)p1
- p=1时,为曼哈顿距离
- p=2时,为欧式距离
对样本特征的旋转和平移变换不敏感,对数值尺度敏感(故需要标准化处理)
-
余弦相似度:两变量看作高维空间的两个向量,两个向量的夹角余弦即为余弦相似度
s ( x i , x j ) = ∑ d = 1 D x i d x j d ∑ d = 1 D x i d 2 ∑ d = 1 D x j d 2 = x i T x j ∥ x i ∥ ∥ x j ∥ s(x_i,x_j)=\frac{\sum_{d=1}^Dx_{id}x_{jd}}{\sqrt{\sum_{d=1}^Dx_{id}^2}\sqrt{\sum_{d=1}^Dx_{jd}^2}}=\frac{x_i^Tx_j}{\Vert x_i \Vert\Vert x_j \Vert} s(xi,xj)=∑d=1Dxid2∑d=1Dxjd2∑d=1Dxidxjd=∥xi∥∥xj∥xiTxj
-
相关系数:当对数据做中心化后,相关系数等于余弦相似度
r ( x i , x j ) = c o v ( x i , x j ) σ x i σ x j = E [ ( x i − μ i ) ( x j − μ j ) ] σ x i σ x j = ∑ d = 1 D ( x i d − μ i d ) ( x j d − μ j d ) ∑ d = 1 D ( x i d − μ i d ) 2 ∑ d = 1 D ( x j d − μ j d ) 2 r(x_i,x_j)=\frac{cov(x_i,x_j)}{\sigma_{x_i}\sigma_{x_j}}=\frac{E[(x_i-\mu_i)(x_j-\mu_j)]}{\sigma_{x_i}\sigma_{x_j}}= \frac{\sum_{d=1}^D(x_{id}-\mu_{id})(x_{jd}-\mu_{jd})}{\sqrt{\sum_{d=1}^D(x_{id}-\mu_{id})^2}\sqrt{\sum_{d=1}^D(x_{jd}-\mu_{jd})^2}} r(xi,xj)=σxiσxjcov(xi,xj)=σxiσxjE[(xi−μi)(xj−μj)]=∑d=1D(xid−μid)2∑d=1D(xjd−μjd)2∑d=1D(xid−μid)(xjd−μjd)
-
杰卡德相似系数
J ( x i , x j ) = ∑ k = 1 D ( x i k ⋂ x j k ) ∑ k = 1 D ( x i k ⋃ x j k ) J(x_i,x_j)=\frac{\sum_{k=1}^D(x_{ik}\bigcap x_{jk})}{\sum_{k=1}^D(x_{ik}\bigcup x_{jk})} J(xi,xj)=∑k=1D(xik⋃xjk)∑k=1D(xik⋂xjk)
1.3 聚类性能评价指标
-
外部评价法:聚类结果与参考结果有多接近
a = # { ( x i , x j ) ∣ x i , x j ∈ C k ; x i , x j ∈ C l ∗ } d = # { ( x i , x j ) ∣ x i ∈ C k 1 , x j ∈ C k 2 ; x i ∈ C l 1 ∗ , x j ∈ C l 2 ∗ } b = # { ( x i , x j ) ∣ x i , x j ∈ C k ; x i ∈ C l 1 ∗ , x j ∈ C l 2 ∗ } c = # { ( x i , x j ) ∣ x i ∈ C k 1 , x j ∈ C k 2 ; x i , x j ∈ C l ∗ } a = \#\{(x_i,x_j)|x_i,x_j\in C_k;x_i,x_j\in C^*_l\} \\ d = \#\{(x_i,x_j)|x_i\in C_{k_1},x_j\in C_{k_2};x_i\in C^*_{l_1},x_j\in C^*_{l_2}\} \\ b = \#\{(x_i,x_j)|x_i,x_j\in C_k;x_i\in C^*_{l_1},x_j\in C^*_{l_2}\} \\ c = \#\{(x_i,x_j)|x_i\in C_{k_1},x_j\in C_{k_2};x_i,x_j\in C^*_l\} a=#{(xi,xj)∣xi,xj∈Ck;xi,xj∈Cl∗}d=#{(xi,xj)∣xi∈Ck1,xj∈Ck2;xi∈Cl1∗,xj∈Cl2∗}b=#{(xi,xj)∣xi,xj∈Ck;xi∈Cl1∗,xj∈Cl2∗}c=#{(xi,xj)∣xi∈Ck1,xj∈Ck2;xi,xj∈Cl∗}
- Jaccard系数: J C = a a + b + c JC =\frac{a}{a+b+c} JC=a+b+ca
- FMI指数: a a + b a a + c \sqrt{\frac{a}{a+b}\frac{a}{a+c}} a+baa+ca
- Rand指数: R I = 2 ( a + d ) N ( N − 1 ) RI=\frac{2(a+d)}{N(N-1)} RI=N(N−1)2(a+d)
-
内部评价法:聚类的本质特点(无参考结果)
簇内相似度越高,聚类质量越好;簇间相似度越低,聚类质量越好。
-
簇内相似度
- 平均距离: a v g ( C m ) = 1 ∣ C m ∣ ( ∣ C m ∣ − 1 ) ∑ x i , x j ∈ C m d i s t ( x i , x j ) avg(C_m)=\frac{1}{|C_m|(|C_m|-1)}\sum_{x_i,x_j \in C_m}dist(x_i,x_j) avg(Cm)=∣Cm∣(∣Cm∣−1)1∑xi,xj∈Cmdist(xi,xj)
- 最大距离: d i a m ( C m ) = m a x x i , x j ∈ C m d i s t ( x i , x j ) diam(C_m)=max_{x_i,x_j\in C_m}dist(x_i,x_j) diam(Cm)=maxxi,xj∈Cmdist(xi,xj)
- 簇的半径: d i a m ( C m ) = 1 ∣ C m ∣ ∑ x i ∈ C m ( d i s t ( x i , μ m ) ) 2 , μ m = 1 ∣ C m ∣ ∑ x i ∈ C m x i diam(C_m)=\sqrt{\frac{1}{|C_m|}\sum_{x_i\in C_m}(dist(x_i,\mu_m))^2},\quad \mu_m=\frac{1}{|C_m|}\sum_{x_i\in C_m}x_i diam(Cm)=∣Cm∣1∑xi∈Cm(dist(xi,μm))2,μm=∣Cm∣1∑xi∈Cmxi
-
簇间相似度
- 最小距离: d m i n ( C m , C n ) = m i n x i ∈ C m , x j ∈ C n d i s t ( x i , x j ) d_{min}(C_m,C_n)=min_{x_i\in C_m,x_j\in C_n}dist(x_i,x_j) dmin(Cm,Cn)=minxi∈Cm,xj∈Cndist(xi,xj)
- 类中心之间的距离: d c e n ( C m , C n ) = d i s t ( μ m , μ n ) , μ m = 1 ∣ C m ∣ ∑ x i ∈ C m x i d_{cen}(C_m,C_n)=dist(\mu_m,\mu_n),\quad \mu_m=\frac{1}{|C_m|}\sum_{x_i\in C_m}x_i dcen(Cm,Cn)=dist(μm,μn),μm=∣Cm∣1∑xi∈Cmxi
-
DB指数:DBI越小,聚类质量越好
D B I = 1 M ∑ m = 1 M max m ≠ n a v g ( C m ) + a v g ( C n ) d c e n ( C m , C n ) DBI=\frac{1}{M}\sum_{m=1}^M\max_{m\neq n}\frac{avg(C_m)+avg(C_n)}{d_{cen}(C_m,C_n)} DBI=M1∑m=1Mmaxm=ndcen(Cm,Cn)avg(Cm)+avg(Cn)
-
Dunn指数:DI越大,聚类质量越好
D I = min 1 ≤ < n ≤ M d m i n ( C m , C n ) max 1 ≤ m ≤ M d i a m ( C m ) DI=\min_{1\le <n\le M}\frac{d_{min}(C_m,C_n)}{\max_{1\le m \le M }diam(C_m)} DI=min1≤<n≤Mmax1≤m≤Mdiam(Cm)dmin(Cm,Cn)
-
2. 常见聚类算法
2.1 K均值聚类算法
伪代码:
输入:n个样本点的集合 { x 1 , x 2 , . . . , x n } \{ x_1,x_2,...,x_n\} {x1,x2,...,xn},聚类中心数目K;
输出:样本集合的聚类 { C 1 , C 2 , . . . , C k } \{{C_1,C_2,...,C_k}\} {C1,C2,...,Ck}
(1)初始化。 t = 0 t=0 t=0,随机选择K个样本点作为聚类中心 m ( 0 ) = ( m 1 ( 0 ) , m 2 ( 0 ) , . . . , m k ( 0 ) ) m^{(0)}=(m^{(0)}_1,m^{(0)}_2,...,m^{(0)}_k) m(0)=(m1(0),m2(0),...,mk(0))
(2)对样本进行聚类。对聚类中心 m ( t ) = ( m 1 ( t ) , m 2 ( t ) , . . . , m k ( t ) ) m^{(t)}=(m^{(t)}_1,m^{(t)}_2,...,m^{(t)}_k) m(t)=(m1(t),m2(t),...,mk(t)),计算每个样本到各个聚类中心的距离,并将其指派到距离最近的中心当中,构成聚类结果 C ( t ) C^{(t)} C(t)
(3)计算新的聚类中心。对于聚类结果 C ( t ) C^{(t)} C(t),计算新的聚类中心 m ( t + 1 ) = ( m 1 ( t + 1 ) , m 2 ( t + 1 ) , . . . , m k ( t + 1 ) ) m^{(t+1)}=(m^{(t+1)}_1,m^{(t+1)}_2,...,m^{(t+1)}_k) m(t+1)=(m1(t+1),m2(t+1),...,mk(t+1))
(4)如果迭代收敛或符合停止条件,输出 C ∗ = C ( t ) C^*=C^(t) C∗=C(t),否则,令 t = t + 1 t=t+1 t=t+1,返回步(2)
从优化角度看待K均值聚类算法的求解:
-
损失函数: J = ∑ i = 1 N ∑ l = 1 K r i k ∥ x i − μ k ∥ 2 J=\sum_{i=1}^N\sum_{l=1}^Kr_{ik}\Vert x_i-\mu_k\Vert^2 J=∑i=1N∑l=1Krik∥xi−μk∥2,其中 r i k r_{ik} rik为从属度
-
采用坐标轴下降法迭代求解 μ k \mu_k μk和 r i k r_{ik} rik
由于 J J J是非凸的,所以坐标下降方法并不一定能保证找到全局最小值
初始化K-means的方法
- 随机初始化
- 随机确定第一个类的中心,其他类的位置尽量远离已有中心
K的选择
- 间隔统计
- 交叉验证
- 簇的稳定性
- 非参数方法
- 用监督学习任务校验集上的评价指标选择K
K-means的局限性
- 没有考虑簇的尺度
- 没有考虑簇的密度
- 没有考虑非球形簇
- 容易受离群点干扰–>K-medoids
2.2 高斯混合模型和EM算法
高斯混合分布有:
p
(
x
∣
θ
)
=
∑
k
=
1
K
π
k
N
(
x
∣
μ
k
,
Σ
k
)
p(x|\theta)=\sum_{k=1}^K\pi_k \mathcal N(x|\mu_k,\Sigma_k)
p(x∣θ)=k=1∑KπkN(x∣μk,Σk)
定义离散隐变量
z
z
z,
z
z
z为
1
−
o
f
−
K
1{-} of{-}K
1−of−K形式的向量,只有某个元素的
z
k
z_k
zk为1,其他元素均为0,
z
z
z与
x
x
x有如下概率图关系:
定义 x x x和 z z z的联合分布 p ( x , z ) p(x,z) p(x,z), z z z的边缘分布 p ( z ) p(z) p(z),条件分布 p ( x ∣ z ) p(x|z) p(x∣z)
依据隐变量
z
z
z的每一个维度对应
x
x
x的每一个维度上是一个高斯分布有:
p
(
z
k
=
1
)
=
π
k
p
(
x
∣
z
k
=
1
)
=
N
(
x
∣
μ
k
,
Σ
k
)
p(z_k=1)=\pi_k\\ p(x|z_k=1)=\mathcal N(x|\mu_k,\Sigma_k )
p(zk=1)=πkp(x∣zk=1)=N(x∣μk,Σk)
则可定义
p
(
z
)
p(z)
p(z)和
p
(
x
∣
z
)
p(x|z)
p(x∣z)有:
p
(
z
)
=
∏
k
=
1
K
π
z
k
p
(
x
∣
z
)
=
∏
k
=
1
K
N
(
x
∣
μ
k
,
Σ
k
)
z
k
p(z)=\prod_{k=1}^K\pi^{z_k}\\ p(x|z)=\prod_{k=1}^K \mathcal N(x|\mu_k,\Sigma_k)^{z_k}
p(z)=k=1∏Kπzkp(x∣z)=k=1∏KN(x∣μk,Σk)zk
则
x
x
x的边缘分布有:
p
(
x
)
=
∑
z
p
(
z
)
p
(
x
∣
z
)
=
∑
k
=
1
K
π
k
N
(
x
∣
μ
k
,
Σ
k
)
\begin{aligned} p(x)&=\sum_z p(z)p(x|z)\\ &=\sum_{k=1}^K\pi_k\mathcal N(x|\mu_k,\Sigma_k) \end{aligned}
p(x)=z∑p(z)p(x∣z)=k=1∑KπkN(x∣μk,Σk)
联合分布有:
p
(
X
,
Z
∣
μ
,
Σ
,
π
)
=
∏
n
=
1
N
∏
k
=
1
K
π
z
n
k
N
(
x
n
∣
μ
k
,
Σ
k
)
n
k
z
p(X,Z|\mu,\Sigma,\pi)=\prod_{n=1}^N\prod_{k=1}^K\pi^{z_{nk}}\mathcal N(x_n|\mu_k,\Sigma_k)^z_{nk}
p(X,Z∣μ,Σ,π)=n=1∏Nk=1∏KπznkN(xn∣μk,Σk)nkz
到此得到了一个包含隐变量的联合分布。同时有后验概率:
γ
(
z
k
=
1
)
=
p
(
z
k
=
1
∣
x
)
=
p
(
z
k
=
1
)
p
(
x
∣
z
k
=
1
)
∑
j
=
1
K
p
(
z
j
=
1
)
p
(
x
∣
z
j
=
1
)
=
π
k
N
(
x
∣
μ
k
,
Σ
k
)
∑
j
=
1
K
π
j
N
(
x
∣
μ
j
,
Σ
j
)
\begin{aligned} \gamma(z_k=1)&=p(z_k=1|x)\\ &=\frac{p(z_k=1)p(x|z_k=1)}{\sum_{j=1}^Kp(z_j=1)p(x|z_j=1)}\\ &=\frac{\pi_k \mathcal N(x|\mu_k,\Sigma_k)}{\sum_{j=1}^K\pi_j \mathcal N(x|\mu_j,\Sigma_j)} \end{aligned}
γ(zk=1)=p(zk=1∣x)=∑j=1Kp(zj=1)p(x∣zj=1)p(zk=1)p(x∣zk=1)=∑j=1KπjN(x∣μj,Σj)πkN(x∣μk,Σk)
2.2.1 最大似然
假设有观测样本集
{
x
1
,
.
.
.
,
x
N
}
\{x_1,...,x_N\}
{x1,...,xN},样本集中每个样本都是独立的从分布
x
x
x中生成的,则可得似然函数:
P
(
X
∣
π
,
μ
,
Σ
)
=
∏
i
=
1
N
p
(
x
i
∣
π
,
μ
,
Σ
)
l
o
g
P
(
X
∣
π
,
μ
,
Σ
)
=
∑
i
=
1
N
l
n
{
∑
k
=
1
K
π
k
N
(
x
i
∣
μ
k
,
Σ
k
)
}
P(X|\pi,\mu,\Sigma)=\prod_{i=1}^Np(x_i|\pi,\mu,\Sigma)\\ logP(X|\pi,\mu,\Sigma)=\sum_{i=1}^Nln\big\{ \sum_{k=1}^K\pi_k\mathcal N(x_i|\mu_k,\Sigma_k)\big\}
P(X∣π,μ,Σ)=i=1∏Np(xi∣π,μ,Σ)logP(X∣π,μ,Σ)=i=1∑Nln{k=1∑KπkN(xi∣μk,Σk)}
最大似然法存在的问题:
-
某个高斯成分可能会坍缩到某个具体的样本点上,此时该成分贡献了无限大的似然值,导致其他高斯成分将几乎没有贡献
-
一个 K K K个成分的混合模型,将有 K ! K! K!个完全相同的最优解,这些解的值是相同的,但对模型的可解释性造成了困难
-
log函数内为多个高斯函数的求和,导致log不能直接作用域单个高斯函数,对求闭式解造成了困难
2.2.2 EM算法求解高斯混合模型的最大似然
似然函数对
μ
k
\mu_k
μk求偏导等于0得:
0
=
−
∑
i
=
1
N
π
k
N
(
x
i
∣
μ
k
,
Σ
k
)
∑
j
K
π
k
N
(
x
i
∣
μ
j
,
Σ
j
)
Σ
k
(
x
i
−
μ
k
)
=
−
∑
i
=
1
N
γ
(
z
i
k
)
Σ
k
(
x
i
−
μ
k
)
\begin{aligned} 0&=-\sum_{i=1}^N\frac{\pi_k\mathcal N(x_i|\mu_k,\Sigma_k)}{\sum_j^K\pi_k\mathcal N(x_i|\mu_j,\Sigma_j)}\Sigma_k(x_i-\mu_k)\\ &=-\sum_{i=1}^N\gamma(z_{ik})\Sigma_k(x_i-\mu_k) \end{aligned}
0=−i=1∑N∑jKπkN(xi∣μj,Σj)πkN(xi∣μk,Σk)Σk(xi−μk)=−i=1∑Nγ(zik)Σk(xi−μk)
解得:
μ
k
=
1
N
k
∑
i
=
1
N
γ
(
z
i
k
)
x
i
N
k
=
∑
i
=
1
N
γ
(
z
i
k
)
\mu_k=\frac{1}{N_k}\sum_{i=1}^N\gamma(z_{ik})x_i\\ N_k=\sum_{i=1}^N\gamma(z_{ik})
μk=Nk1i=1∑Nγ(zik)xiNk=i=1∑Nγ(zik)
可以解释
N
k
N_k
Nk为被分到簇
k
k
k得点得数目。
似然函数对
Σ
k
\Sigma_k
Σk求偏导等于0得:
Σ
k
=
1
N
k
∑
i
=
1
N
γ
(
z
i
k
)
(
x
i
−
μ
k
)
(
x
i
−
μ
k
)
T
\Sigma_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(z_{ik})(x_i-\mu_k)(x_i-\mu_k)^T
Σk=Nk1i=1∑Nγ(zik)(xi−μk)(xi−μk)T
求解
π
k
\pi_k
πk需要满足约束
∑
k
=
1
N
π
k
=
1
\sum_ {k=1}^N\pi_k=1
∑k=1Nπk=1,采用拉格朗日乘子法有:
l
n
p
(
X
∣
π
,
μ
,
Σ
)
+
λ
(
∑
k
=
1
K
π
k
−
1
)
lnp(X|\pi,\mu,\Sigma)+\lambda\bigg(\sum_{k=1}^K\pi_k-1\bigg)
lnp(X∣π,μ,Σ)+λ(k=1∑Kπk−1)
对
π
k
\pi _k
πk求导等于0得:
0
=
∑
i
=
1
N
N
(
x
i
∣
μ
k
,
Σ
k
)
∑
j
K
π
k
N
(
x
i
∣
μ
j
,
Σ
j
)
+
λ
0 =\sum_{i=1}^N\frac{\mathcal N(x_i|\mu_k,\Sigma_k)}{\sum_j^K\pi_k\mathcal N(x_i|\mu_j,\Sigma_j)}+\lambda
0=i=1∑N∑jKπkN(xi∣μj,Σj)N(xi∣μk,Σk)+λ
解的:
π
k
=
N
k
N
\pi_k=\frac{N_k}{N}
πk=NNk
因为
γ
(
z
i
k
)
\gamma(z_{ik})
γ(zik)以一种复杂的方式依赖
μ
k
,
Σ
k
,
π
k
\mu _k,\Sigma_k,\pi_k
μk,Σk,πk,故这样得出来的
μ
k
,
Σ
k
,
π
k
\mu _k,\Sigma_k,\pi_k
μk,Σk,πk并不构成一个闭式解,但给出了一种迭代机制来找出最大似然的解,即EM算法。
用于高斯混合模型的EM算法
初始化 μ k , Σ k , π k \mu_k,\Sigma_k,\pi_k μk,Σk,πk,估计似然函数的初始值
E step. 计算从属度(责任值)
γ ( z k = 1 ) = π k N ( x ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x ∣ μ j , Σ j ) \gamma(z_k=1)=\frac{\pi_k \mathcal N(x|\mu_k,\Sigma_k)}{\sum_{j=1}^K\pi_j \mathcal N(x|\mu_j,\Sigma_j)} γ(zk=1)=∑j=1KπjN(x∣μj,Σj)πkN(x∣μk,Σk)M step. 使用当前责任值重新估计参数
μ k = 1 N k ∑ i = 1 N γ ( z i k ) x i Σ k = 1 N k ∑ i = 1 N γ ( z i k ) ( x i − μ k ) ( x i − μ k ) T π k = N k N w h e r e N k = ∑ i = 1 N γ ( z i k ) \mu_k=\frac{1}{N_k}\sum_{i=1}^N\gamma(z_{ik})x_i\\ \Sigma_k = \frac{1}{N_k}\sum_{i=1}^N\gamma(z_{ik})(x_i-\mu_k)(x_i-\mu_k)^T\\ \pi_k=\frac{N_k}{N}\\ where\quad N_k=\sum_{i=1}^N\gamma(z_{ik}) μk=Nk1i=1∑Nγ(zik)xiΣk=Nk1i=1∑Nγ(zik)(xi−μk)(xi−μk)Tπk=NNkwhereNk=i=1∑Nγ(zik)计算似然函数值
l o g P ( X ∣ π , μ , Σ ) = ∑ i = 1 N l n { ∑ k = 1 K π k N ( x i ∣ μ k , Σ k ) } logP(X|\pi,\mu,\Sigma)=\sum_{i=1}^Nln\big\{ \sum_{k=1}^K\pi_k\mathcal N(x_i|\mu_k,\Sigma_k)\big\} logP(X∣π,μ,Σ)=i=1∑Nln{k=1∑KπkN(xi∣μk,Σk)}
检查参数或似然函数值的收敛性没,如果不满足收敛检验则回到step 2
2.2.3 一般形式的EM算法
EM算法是一种迭代式算法,用于含有隐变量的概率参数模型的最大似然估计或极大后验概率估计,核心思想是用观测数据
X
X
X和现有模型
θ
\theta
θ估计隐变量的后验概率,再用隐变量的后验概率计算似然函数的期望来替换似然函数(对这个式子2.2.4有更漂亮的理论解释):
max
l
n
P
(
X
,
Z
∣
θ
)
=
max
∑
z
P
(
z
∣
X
,
θ
o
l
d
)
l
n
P
(
X
,
z
∣
θ
)
\begin{aligned} \max lnP(X,Z|\theta)=\max\sum_zP(z|X,\theta^{old})lnP(X,z|\theta) \end{aligned}
maxlnP(X,Z∣θ)=maxz∑P(z∣X,θold)lnP(X,z∣θ)
一般形式的EM算法
给出观测变量 X X X和隐变量 Z Z Z在参数 θ \theta θ统治下的联合分布 p ( X , Z ∣ θ ) p(X,Z|\theta) p(X,Z∣θ),目标是寻找 θ \theta θ使得似然函数 p ( X ∣ θ ) p(X|\theta) p(X∣θ)最大
初始化参数 θ o l d \theta^{old} θold
E step 计算 p ( Z ∣ X , θ o l d ) p(Z|X,\theta^{old}) p(Z∣X,θold)
M step 计算
θ n e w = arg max θ { Q ( θ , θ o l d ) 最 大 似 然 估 计 Q ( θ , θ o l d ) + l n p ( θ ) 最 大 后 验 估 计 Q ( θ , θ o l d ) = ∑ Z P ( Z ∣ X , θ o l d ) l n P ( X , Z ∣ θ ) \theta^{new}=\underset{\theta}{\operatorname{arg\,max}}\, \begin{cases} \mathcal Q(\theta,\theta^{old}) \quad 最大似然估计&\\ \mathcal Q(\theta,\theta^{old}) +lnp(\theta) \quad 最大后验估计 \end{cases}\\ \mathcal Q(\theta,\theta^{old})=\sum_ZP(Z|X,\theta^{old})lnP(X,Z|\theta) θnew=θargmax{Q(θ,θold)最大似然估计Q(θ,θold)+lnp(θ)最大后验估计Q(θ,θold)=Z∑P(Z∣X,θold)lnP(X,Z∣θ)检查似然函数或者参数是否满足收敛条件,如果不满足$\theta^{old} \leftarrow \theta $ 回到step 2
2.2.4 更理论化的EM算法
有观测变量
X
X
X、离散隐变量
Z
Z
Z和由参数$\theta
控
制
的
联
合
分
布
控制的联合分布
控制的联合分布p(X,Z|\theta )$,目标是求边际分布的最大似然:
p
(
X
∣
θ
)
=
∑
Z
p
(
X
,
Z
∣
θ
)
p(X|\theta)=\sum_Zp(X,Z|\theta)
p(X∣θ)=Z∑p(X,Z∣θ)
假定直接优化
p
(
X
∣
θ
)
p(X|\theta )
p(X∣θ)是困难的,但是优化
p
(
X
,
Z
∣
θ
)
p(X,Z|\theta )
p(X,Z∣θ)较容易,则log似然可以分解得到:
ln
p
(
X
∣
θ
)
=
L
(
q
,
θ
)
+
K
L
(
q
∣
∣
p
)
L
(
q
,
θ
)
=
∑
Z
q
(
Z
)
ln
{
p
(
X
,
Z
∣
θ
)
q
(
Z
)
}
K
L
(
q
∣
∣
p
)
=
−
∑
Z
q
(
Z
)
ln
{
p
(
Z
∣
X
,
θ
)
q
(
Z
)
}
\ln p(X|\theta) = \mathcal L(q,\theta)+KL(q||p)\\ \mathcal L(q,\theta) = \sum_Zq(Z)\ln \bigg\{\frac{p(X,Z|\theta)}{q(Z)}\bigg\}\\ KL(q||p)=-\sum_Zq(Z)\ln\bigg\{\frac{p(Z|X,\theta)}{q(Z)}\bigg\}
lnp(X∣θ)=L(q,θ)+KL(q∣∣p)L(q,θ)=Z∑q(Z)ln{q(Z)p(X,Z∣θ)}KL(q∣∣p)=−Z∑q(Z)ln{q(Z)p(Z∣X,θ)}
又
K
L
(
p
∣
∣
q
)
≥
0
KL(p||q)\ge0
KL(p∣∣q)≥0,则
ln
p
(
X
∣
θ
)
≥
L
(
q
,
θ
)
\ln p(X|\theta)\ge \mathcal L(q,\theta)
lnp(X∣θ)≥L(q,θ),即$ \mathcal L(q,\theta)
为
为
为\ln p(X|\theta)$的下界
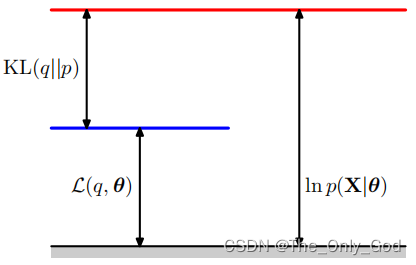
-
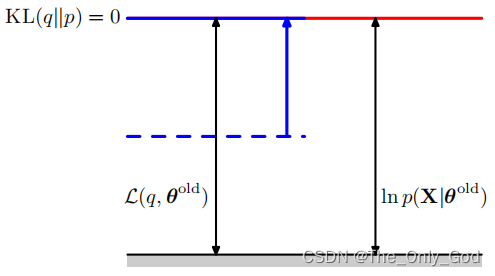
E步: θ o l d \theta^{old} θold固定,优化 q ( Z ) q(Z) q(Z)来使$ \mathcal L(q,\theta)$最大
ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ)不依赖于 q ( Z ) q(Z) q(Z),所以当 K L ( p ∣ ∣ q ) = 0 KL(p||q)=0 KL(p∣∣q)=0时, L ( q , θ ) \mathcal L(q,\theta) L(q,θ)有最大,此时 q ( Z ) = p ( Z ∣ X , θ o l d ) q(Z)=p(Z|X,\theta^{old}) q(Z)=p(Z∣X,θold)
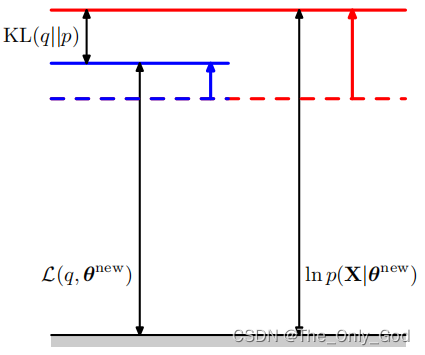
- M步:
q
(
Z
)
q(Z)
q(Z)固定,优化
θ
\theta
θ来增大$ \mathcal L(q,\theta)
,
由
于
,由于
,由于KL(p||q)\ge0
,
所
以
,所以
,所以 \mathcal L(q,\theta)$的增大也导致似然的下界增大
L ( q , θ ) = ∑ Z p ( Z ∣ X , θ o l d ) ln p ( X , Z ∣ θ ) − ∑ Z p ( Z ∣ X , θ o l d ) ln p ( Z ∣ X , θ o l d ) = Q ( θ , θ o l d ) + c o n s t \begin{aligned} \mathcal L(q,\theta)&=\sum_Zp(Z|X,\theta^{old})\ln p(X,Z|\theta)-\sum_Zp(Z|X,\theta^{old})\ln p(Z|X,\theta^{old})\\ &= \mathcal Q(\theta,\theta^{old})+const \end{aligned} L(q,θ)=Z∑p(Z∣X,θold)lnp(X,Z∣θ)−Z∑p(Z∣X,θold)lnp(Z∣X,θold)=Q(θ,θold)+const
同理,当问题为求解最大后验概率时有:
ln
p
(
θ
∣
X
)
=
L
(
q
∣
θ
)
+
K
L
(
p
∣
∣
q
)
+
ln
p
(
θ
)
−
ln
p
(
X
)
≥
L
(
q
,
θ
)
+
ln
p
(
θ
)
−
ln
p
(
X
)
\begin{aligned} \ln p(\theta|X)&=\mathcal L(q|\theta)+KL(p||q)+\ln p(\theta)-\ln p(X)\\ &\ge \mathcal L(q,\theta)+\ln p(\theta)-\ln p(X) \end{aligned}
lnp(θ∣X)=L(q∣θ)+KL(p∣∣q)+lnp(θ)−lnp(X)≥L(q,θ)+lnp(θ)−lnp(X)
求解时,只需稍微修改M步就行
广义EM算法:在M步用仅仅优化部分参数增大 L ( q , θ ) \mathcal L(q,\theta) L(q,θ)就行,来替代优化所有参数来求最大的 L ( q , θ ) \mathcal L(q,\theta) L(q,θ)
增量式EM算法:在一次EM循环中仅处理一个数据点,收敛更快
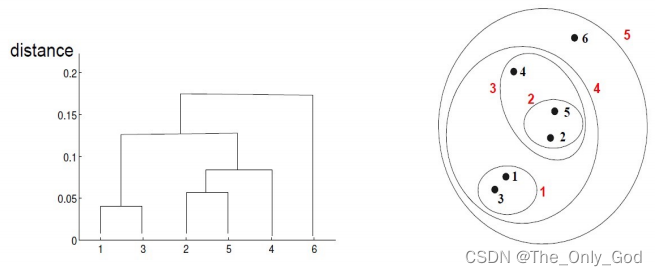
2.3 层次聚类
在不同层次对数据集进行划分,从而形成树形的聚类结构
-
自底向上(凝聚式):递归的合并相似度最高/距离最近的两个簇
-
自顶向下(分裂式):递归地分裂最不一致地簇
簇间相似度计算方式:
- 最小距离:可以形成非球形、非凸地簇;但会有链式效应
- 最大距离:对噪声更加鲁棒(不成链);但趋向于拆开大的簇,偏好球形簇
- 平均距离:MIN和MAX的折中方案
- 中心点距离:存在反向效应问题(后边合并的簇间距离可能比之前合并的簇间距离更近)
- 其他由某种函数推导出来地方法:Ward’s方法等
层次聚类特点
- 不需要提前假定聚类的簇数,用户可以在层次化的聚类中选择一个分割,得到一个最自然的聚类结果
- 聚类结果可能对应着有意义的分类体系
- 一旦簇被合并或拆分,过程不可逆
- 没有优化一个全局的目标函数
- 不同具体实现方法可能存在如下问题:对噪声和离群点敏感、比较难处理不同尺寸的簇和凸的簇、成链误把大簇分裂
2.4 基于密度聚类
此类算法通过假设聚类结构能通过样本分布的紧密程度确定,通常情况下从样本密度的角度考虑样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的结果。
基本概念:
- 核心点:半径 ϵ \epsilon ϵ内多于指定数量 M i n P t s MinPts MinPts个点
- 边界点:半径 ϵ \epsilon ϵ内少于指定数量 M i n P t s MinPts MinPts个点,但在某个核心点的邻域内
- 噪声点:核心点和边界点之外的点
- 密度直达:若 x j x_j xj位于核心点 x i x_i xi的邻域内,则称 x j x_j xj由 x i x_i xi密度直达
- 密度可达:连接 p p p和 q q q的路径上的点都是核心点,则称 q q q由 p p p密度可达
- 密度相连:存在点 o o o其密度可达 p p p和 q q q,则称 p p p和 q q q密度相连
聚类簇满足的性质:
- 连接性:簇内任意两点是密度相连的
- 最大性:如果一个点从一个簇中的任意一点密度可达,则该点属于该簇

基于密度聚类算法的特点:
- 优势
- 不需要明确簇的数量
- 可以适应任意形状的簇
- 对离群点较为鲁棒
- 劣势
- 参数选择较为困难( M i n P t s , ϵ MinPts,\epsilon MinPts,ϵ)
- 不适合密度差异较大的数据集
参考资料
《Pattern Recognition and Machine Learning》
《机器学习》,周志华



![[附源码]计算机毕业设计springboot企业售后服务管理系统](https://img-blog.csdnimg.cn/a45a733a9a544b929a9629e3d76cfe87.png)

![[附源码]SSM计算机毕业设计学校失物招领系统JAVA](https://img-blog.csdnimg.cn/36a162b5aa4e4f85afe4536bf1d00495.png)






![[附源码]计算机毕业设计JAVA线上图书销售管理系统](https://img-blog.csdnimg.cn/ab9288178b974835b1e8f79c3b621c45.png)