背包问题

题目

0-1背包问题:给定n种物品和一背包。物品à的重量是w;,其价值为v; ,背包的容量为C。问:应该如何选择装入背包的物品,使得装入背包中物品的总价值最大?

最优解结构性质

W[n]={w1,w2,...wn};//重量数组
V[n]={v1,v2,...vn};//价值数组
X[n]={x1,x2,...xn};//结果数组

该问题可以总结为该数学公式

SUM(wi*xi)<=C 
&&
MAX(SUM(vi*xi));

在选择装入背包的物品时,对每种物品i只有两种选择,即装入背包或不装人背包。不能将物品i装入背包多次,也不能只装人部分的物品i。因此,该问题称为0-1背包问题，分析时，还是用分治策略，缩小规模，从后面砍数据，将最后一个物品去除

SUM(wi*xi)<=C-wn-1;i=1,2,..n-1;
 &&
MAX(SUM(vi*xi));i=1,2,..n-1;

用m[i][j]来表示当装了i个物品后，背包剩余的空间大小为j时，此时背包中物品的最大价值

注意： i不是一个点值，而是一个区域值，从 0 1 …到i

状态转移方程

方程

i==1时
- m[1][j]=j>w[1]?v[1]:0
i>1时，考虑是否能放下，考虑放不放两种选择，
- 放不下的话
  - m[i][j]=m[i-1][j]
- 能放下考虑最大值
  - m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i])

理解

当只有一个物品时，看能不能放下，能放下，就有价值，否则价值为0
多个物品时，看第i个物品能否放下，取决于背包的剩余容量，
**如果放不下，**价值就和i-1时一样，
**能放下，**要考虑放不放，放的话，价值增加，但是就占了空间，可能导致后面性价比高的东西放不下了，所以此时需要取最大值

不放入背包时:第i次决策后的最大价值和第i-1次决策时候的价值是一样的还是原来的那些物体，没多没少。
放入背包时:第i次决策后的价值为第i-1次决策时候的价值加上当前物体的价值v[j]。物体放入背包前背包容量变为 j ，放入后，容量就会变小j-w[i],即此时价值为前一个物品放入时，剩余容量为j-w[i]时的价值

递归实现

核心思想

刚开始物品比较多，每次都依赖于前面的价值，每次都在缩小规模，等缩小到底部时，再依次回溯，得出结果

代码实现

int Knapsance(int* V, int* W, int i, int n,int j) {
	if (i == 1) {
		if (j >= W[i]) return V[i];
		else return 0;
	}
	else {
		if (j < W[i]) {
			return Knapsance(V, W, i - 1, n, j);
		}
		else {
			int v1 = Knapsance(V, W, i - 1, n, j);
			int v2 = Knapsance(V, W, i - 1, n, j - W[i]) + V[i];
			if (v1 > v2)return v1;
			else return v2;
		}
	}
}

用例测试

int main() {
	const int n = 5;
	const int c = 10;
	int W[n + 1] = { 0,2,2,6,5,4 };
	int V[n + 1] = { 0,6,3,5,4,6 };
	vector<vector<int> >m(n + 1, vector<int>(c + 1, 0));
	int maxv = Knapsance(V, W, n,n , c);
	cout << maxv;
	return 0;
}

输出结果为15

画表非递归实现

核心思路

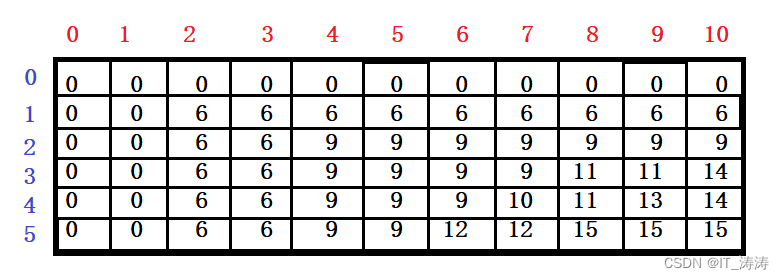
从底部向上记录，根据动归表达式，自底向上记录。先初始化第一行第一列，然后根据动归表达式依次填写。
int W[n + 1] = { 0,2,2,6,5,4 };
0 1 2 3 4 5
int V[n + 1] = { 0,6,3,5,4,6 };

代码实现

int NiceKnapsance2(int* V, int* W, int n, int c, vector<vector<int> >& m) {
	for (int j = 1; j <= c; j++) {
		m[1][j] = j > W[1] ? V[1] : 0;
	}
	PrintVector(m);
	for (int i = 1; i<=n; i++) {
		for (int j = 1; j <= c; j++) {
			if (j < W[i]) {
				m[i][j] = m[i - 1][j];
			}
			else {
				m[i][j] = std::max(m[i - 1][j], m[i - 1][j - W[i]] + V[i]);
			}
		}
		PrintVector(m);
	}
	return m[n][c];
}

画表展示

在这里插入图片描述

计算哪些物品放入

算法思想

根据画的表，进行回溯，标记求解

代码实现

void Traceback(vector<vector<int>>& m, int W[], int n, int c, bool X[]) {
	for (int i = n; i >= 1; i--) {
		if (m[i][c] != m[i-1][c]) {
			X[i] = true;
			c = c - W[i];
		}
	}
}