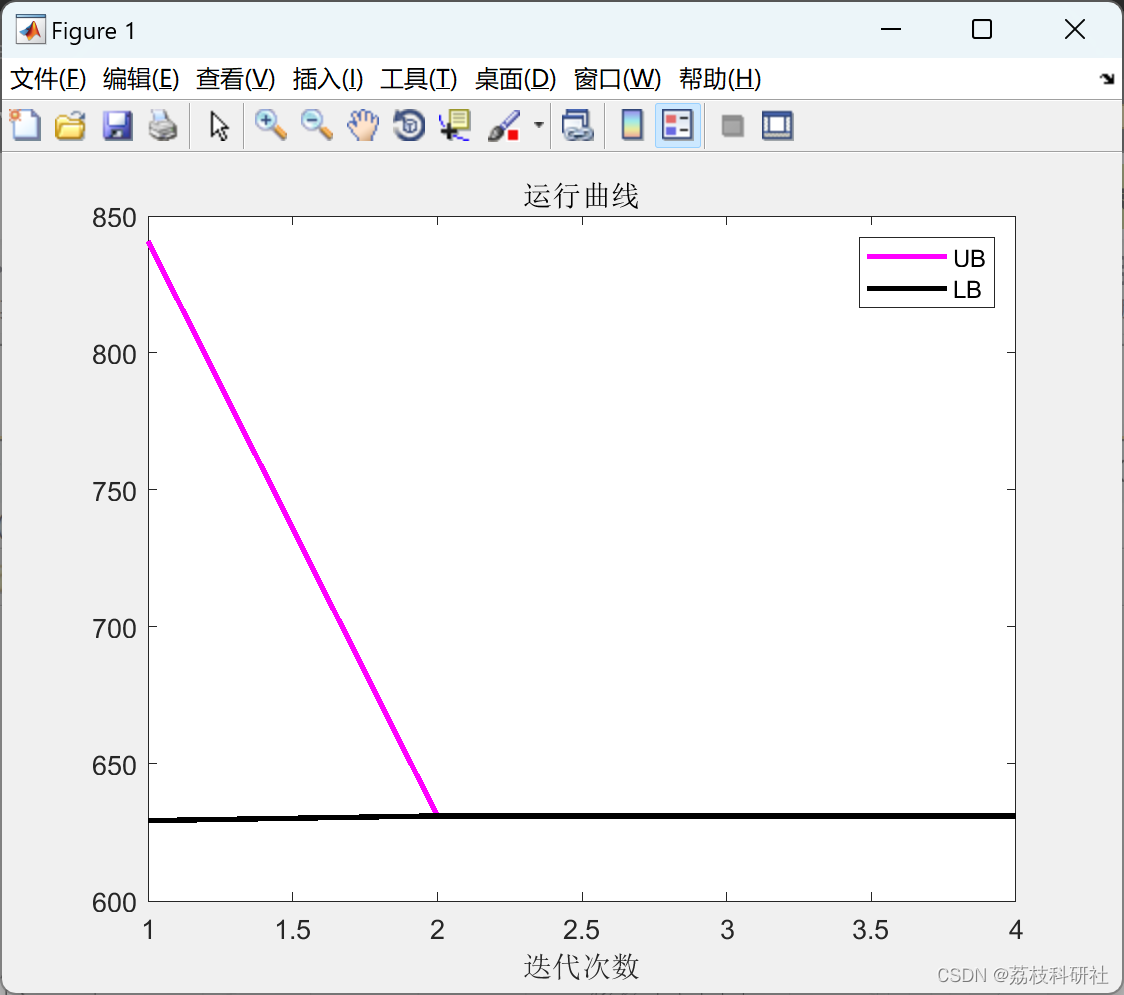
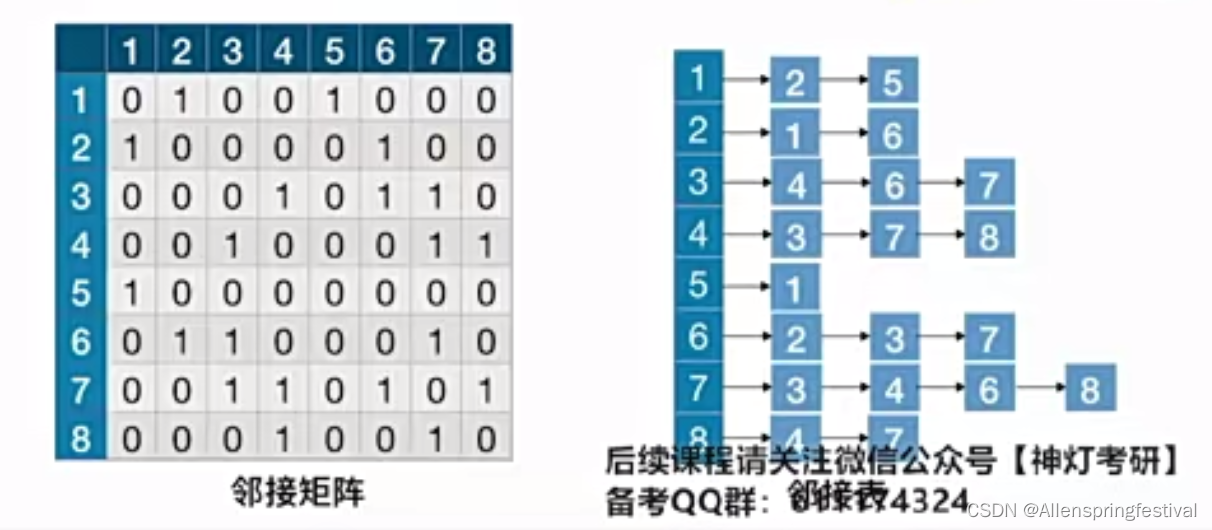
6.2.4图的基本操作

 

考研里面只考邻接矩阵和邻接表的存储结构

 思想较为简单见video

重点理解时间复杂度的遍历原理

6.3.1图的广度优先遍历（BFS）（Breadth first traversal）

我们从树的广度优先遍历入手去看图的广度优先遍历的思想

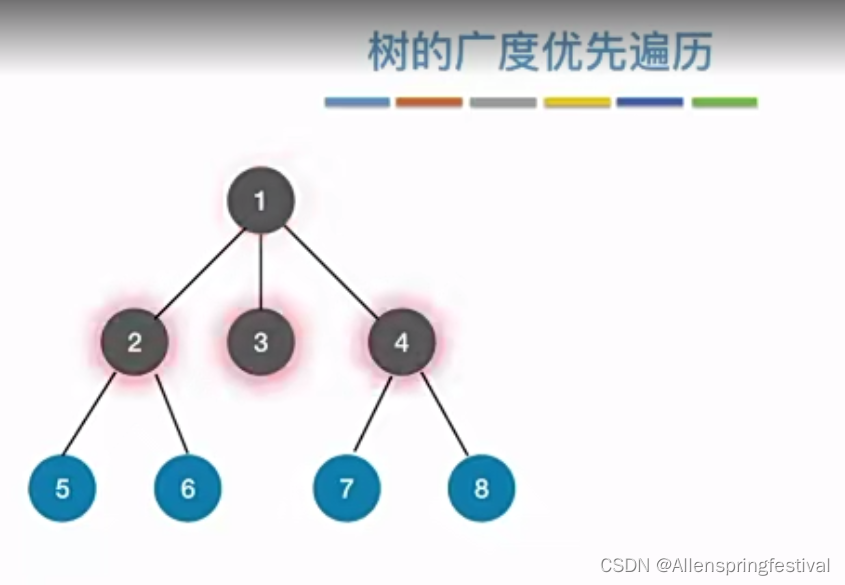
 首先从1根节点开始，向着孩子节点234，

6.3.1图的广度优先遍历

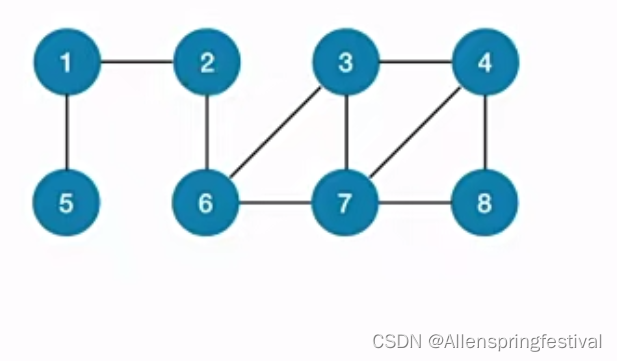
加入先从2结点出发，到1，6结点，接着从1，6结点出发，就是遍历到537.

再从5，3，7出发就是到4，8。

树VS图

 

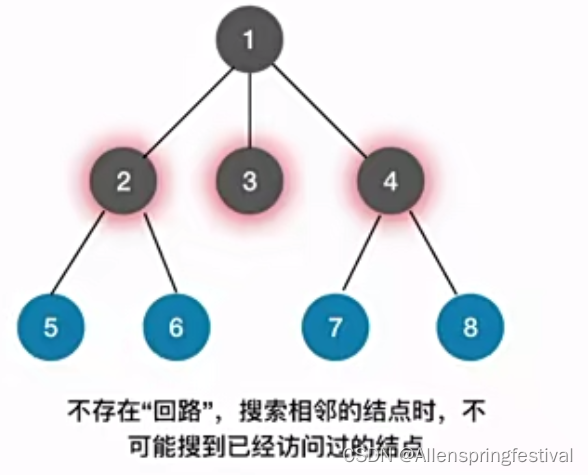
就比如说从6号结点搜索相邻的结点的时候（237），会搜索到已经访问过的结点2。

我们就需要对已经访问过的节点进行标记。

 1.找到与一个顶点相邻的的所有顶点

 应用这两个函数

邻接矩阵和邻接表法实现起来会有所区别：

 2.标记那些顶点被访问过

用一个布尔类型的数组进行存储，该节点是否被访问过。

 

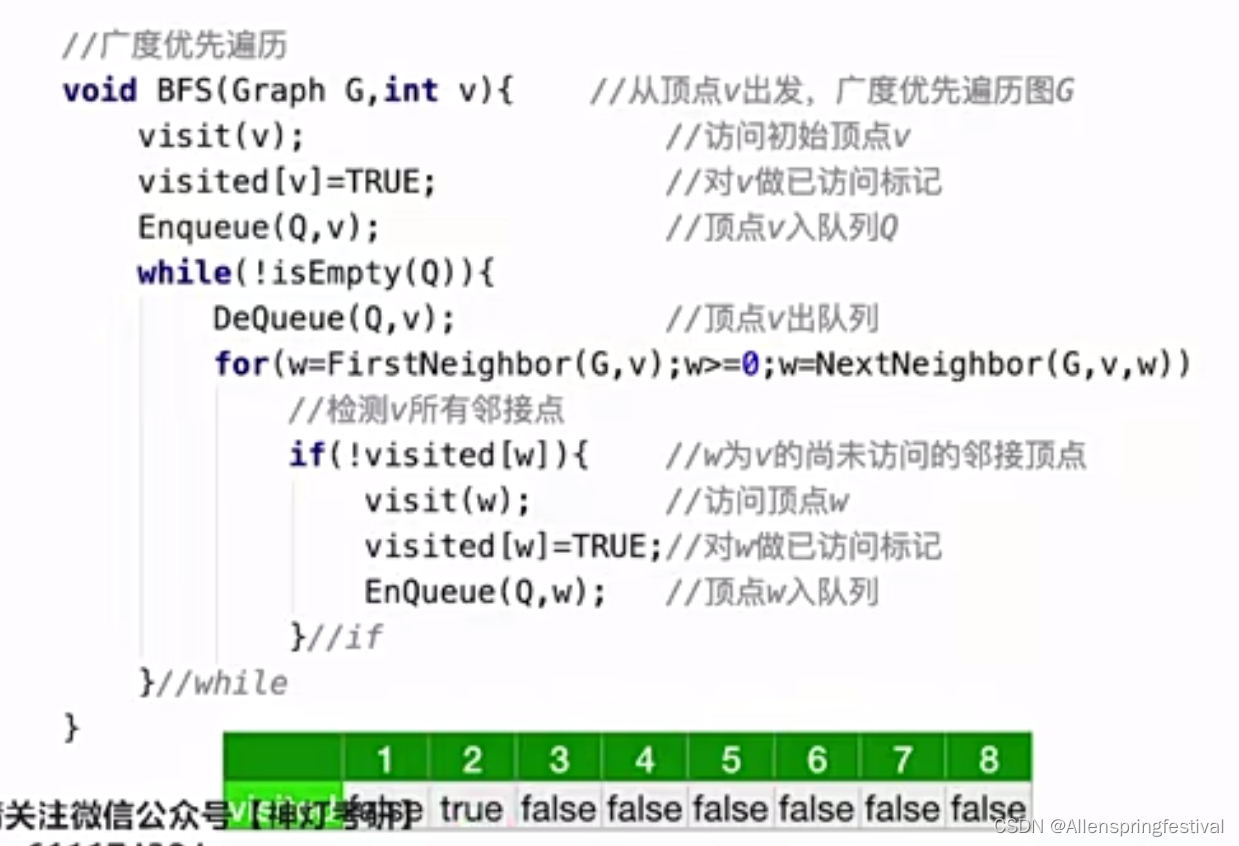
一考试VISITED数组都为false，当元素入队以后对应的序号的数组值就变为True。

 接着DeQueue让2号结点出列，用FirstNeighbour和NextNeighbour进行遍历。

如果对用visited数组值为false，就访问这个结点，并对这个节点作标记，让他入队列。

 接着让一号节点出队，处理1号结点的邻接结点。

 

 

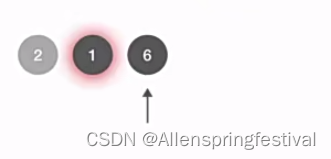
 接着处理队头结点6号结点,DeQueue先出队6，再把237为6的邻接结点，由于2对应的visitd已经为True，所以我把37放入队尾。

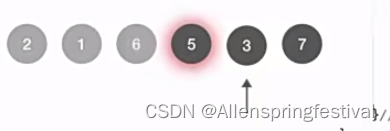
 接下来处理5号结点，5号结点的邻接结点已经被访问过。

 

 接下来处理3号结点，出队，只有4号节点是没有被访问过的。

那如果是从顶点1出发进行广度优先遍历呢？

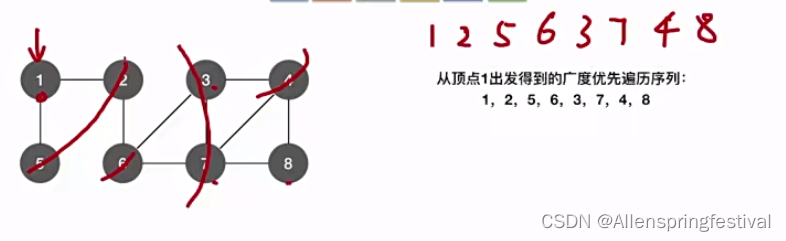
 邻接结点我们是按照顶点递增的次序来排列的，所以1之后是25而不是52.

算法当为非连通图时，会存在问题，无法遍历完所有顶点。

 我们可以对之前的算法进行封装，命名为BFS(Graph G,int v)

然后再BFSTraverse（breadth first search）调用BFS函数从0号结点开始遍历。

从1号结点出发，我们可以Traverse  1-8号结点。

 第一次调用玩BFS函数之后，1-8数组的值都变为了True。

接着会继续往后遍历，直到遍历到9号结点。

 

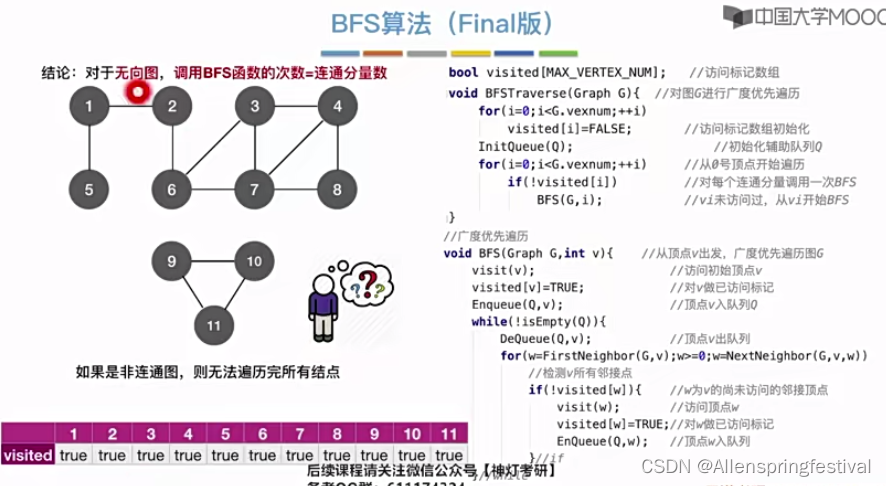这个无向图有两个极大连通子图，也就是两个连通分量，所以需要调用两次广度第一次寻找算法。

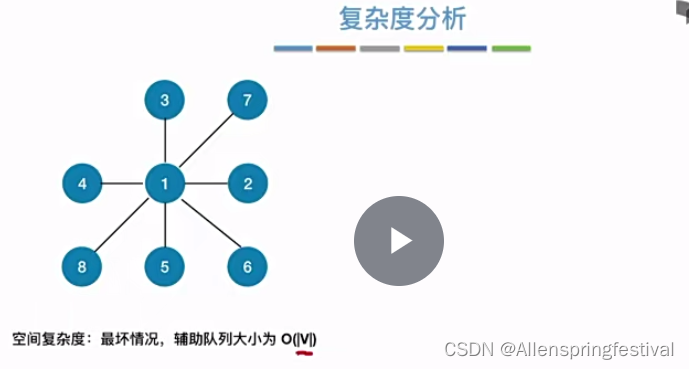
空间复杂度主要来源于辅助队列。

假如我们访问的1号结点，其他所有结点我们都需要放到辅助队列当中 。（最坏情况）

 

 

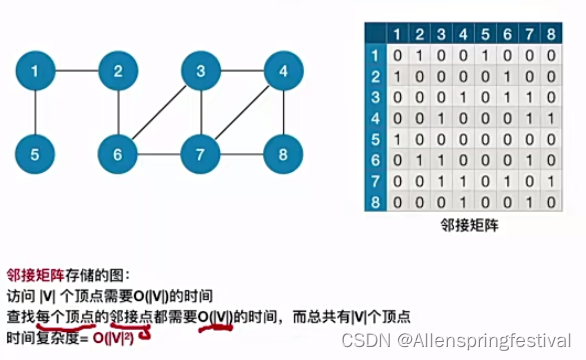
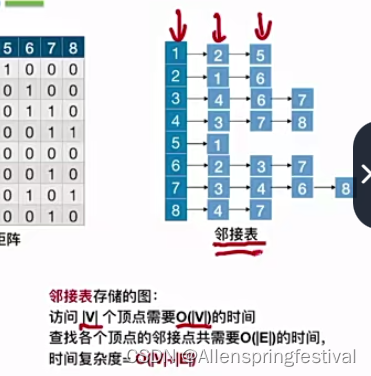
因为无向图一共有2E个边（E为vertex顶点的个数）

时间复杂度主要来源于访问各个顶点，遍历各个边。

接下来我们介绍广度优先生成树

 

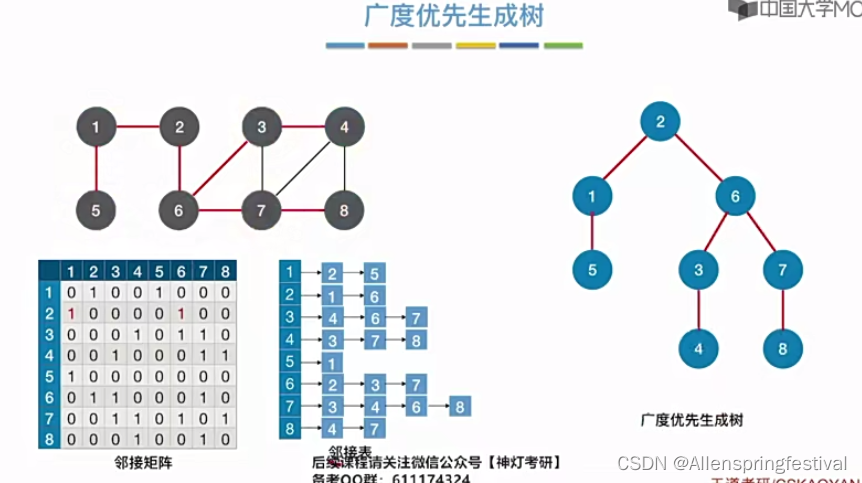
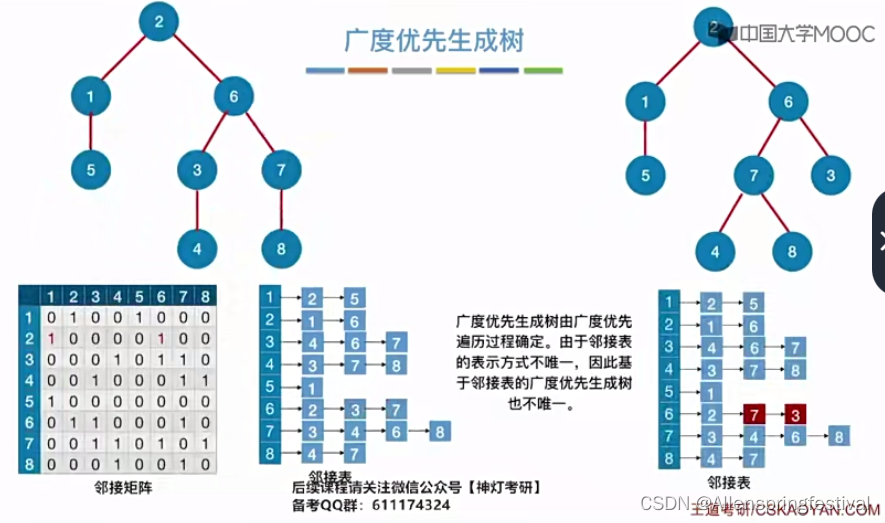
 我们可修改一下6号结点的邻接结点的访问次序，先访问7后访问3，生成树会有所改变。

由于邻接表的表示方式不唯一，因此基于邻接表的广度优先生成树也不唯一。

 

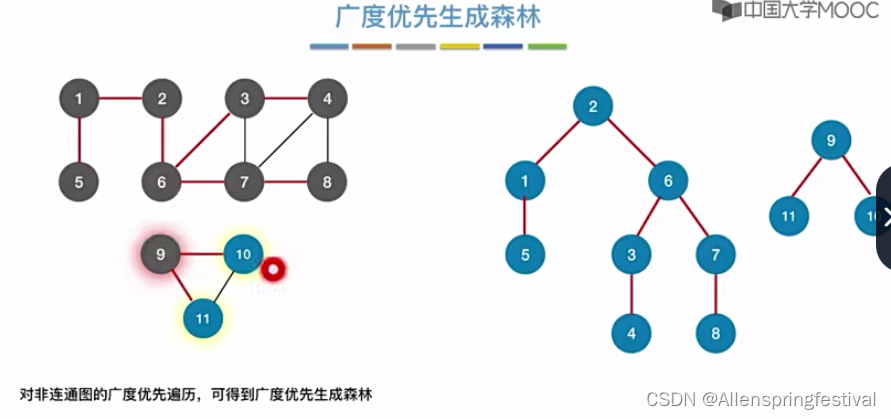
相近的概念：广度优先生成森林（多个连通分量）

 

 

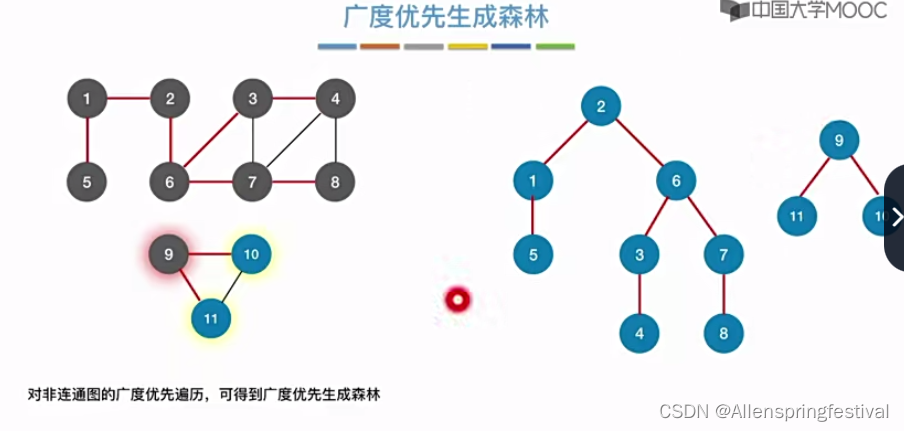
算法要点：

（1）需要一个辅助队列

（2）如何从一个结点找到与之相邻接的其他顶点

（3）visited数组防止重复访问

（4）如何处理非联通图（在设计一个for循环）

 

6.3.2图的深度优先遍历

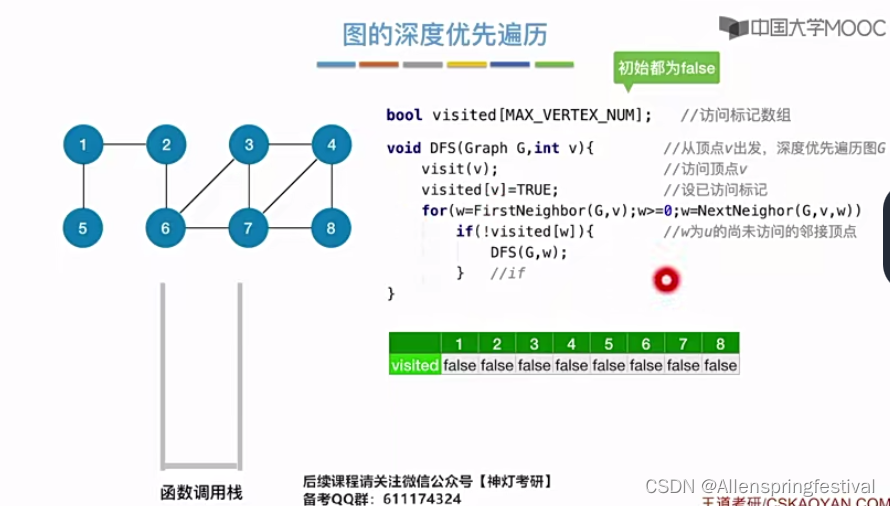
我们需要先来复习一下图的深度优先遍历

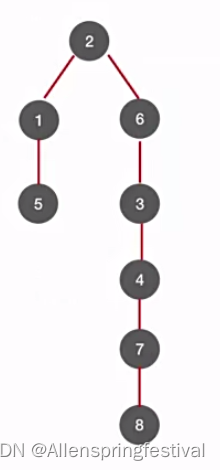
从遍历结点1到节点2到节点5，没有下一个子树。

 访问结点6，返回上一层循环。

 

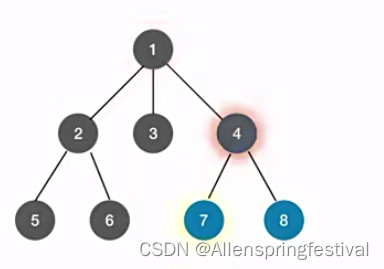
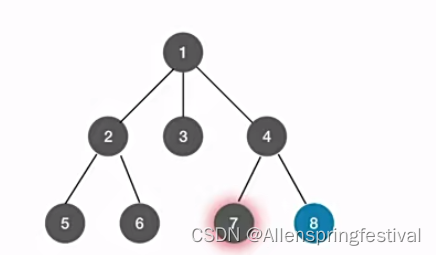
 7没有子树会跳出这一层的递归，返回4这一层的递归继续访问4的子树

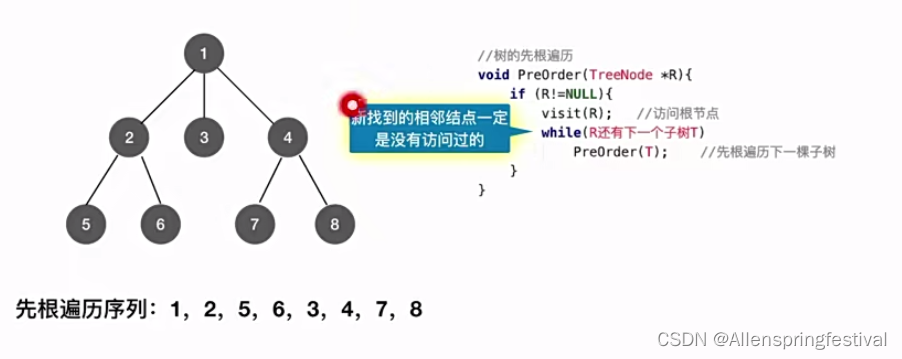
接下来我们介绍图的深度优先遍历（类似）

 

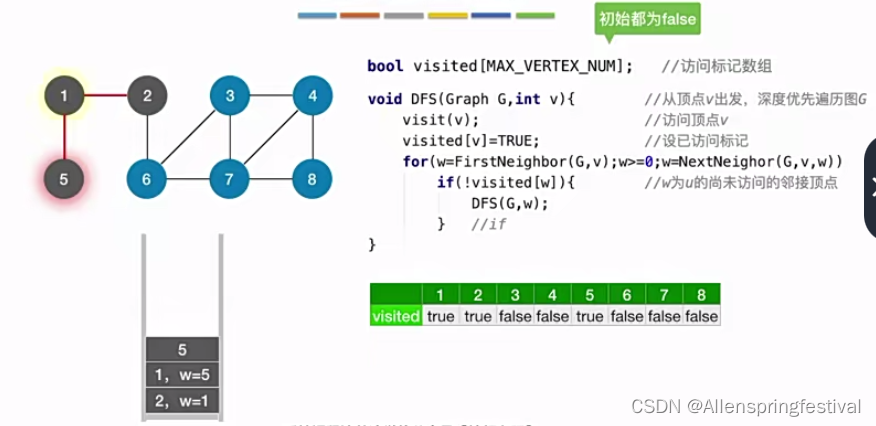
 从2号结点出发，访问1节点，再从1节点访问5号节点。

由于和5号结点相连的所有节点都被访问过了，所以什么也不会做。

 

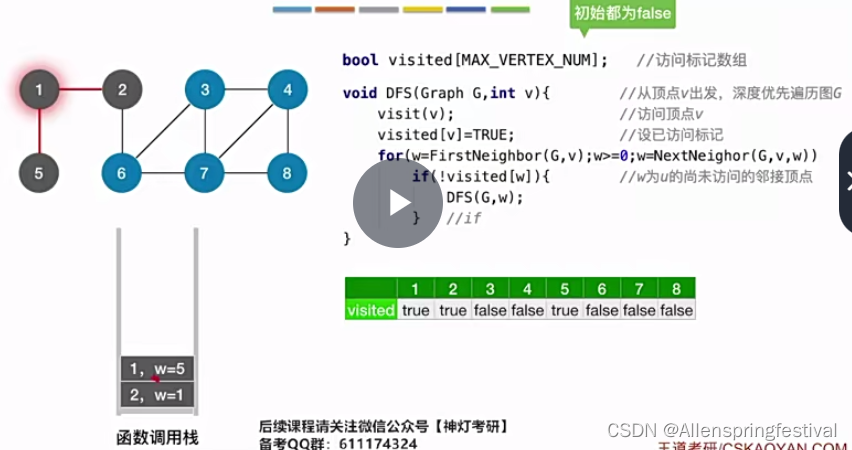
就会返回上一层节点的递归调用，就是1号节点这一层。

 

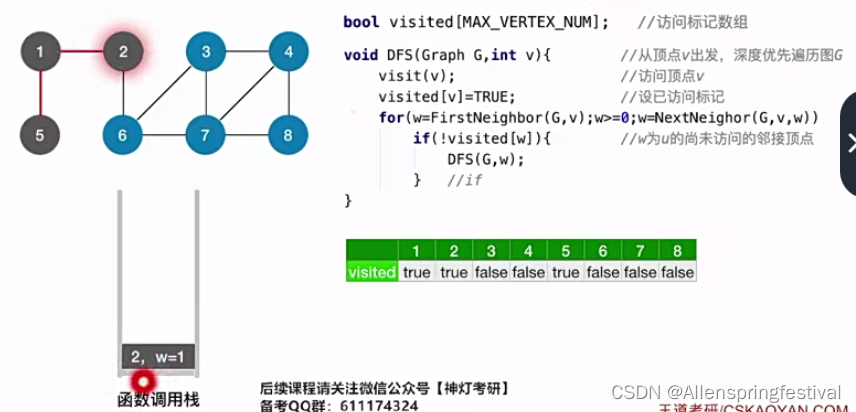
再返回2号节点这一层，之前只访问了一个邻接点，还可以访问邻接顶点6号节点。/

 

 

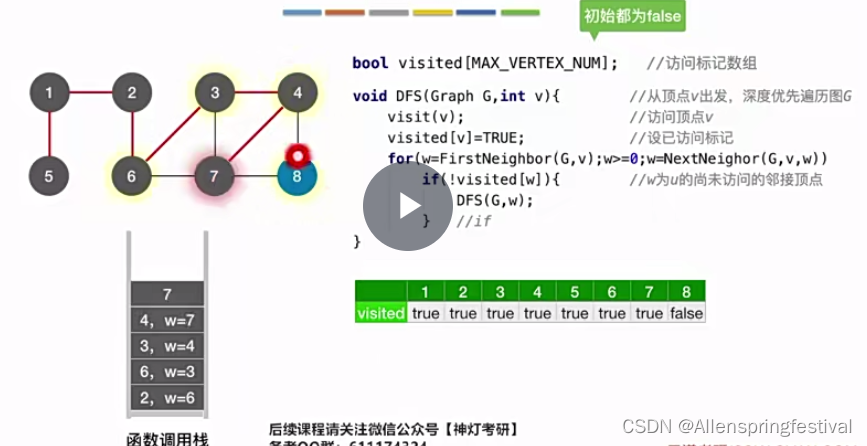
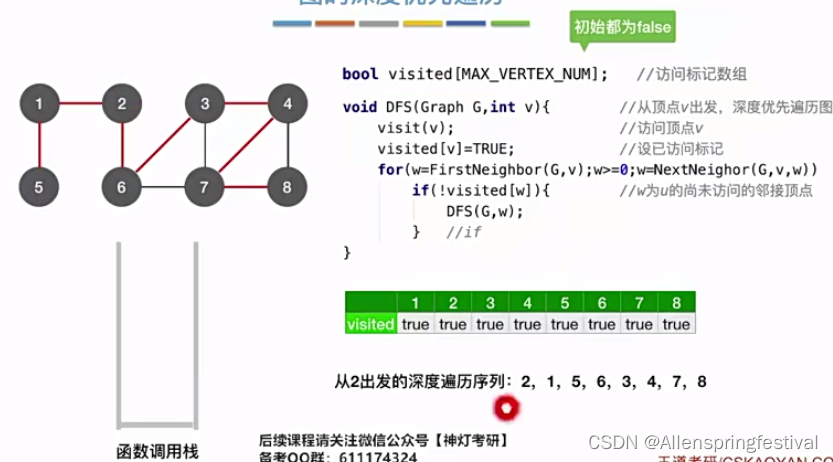 和广度优先遍历得到的序列排序还是有区别的。

复杂度分析：

空间复杂度：

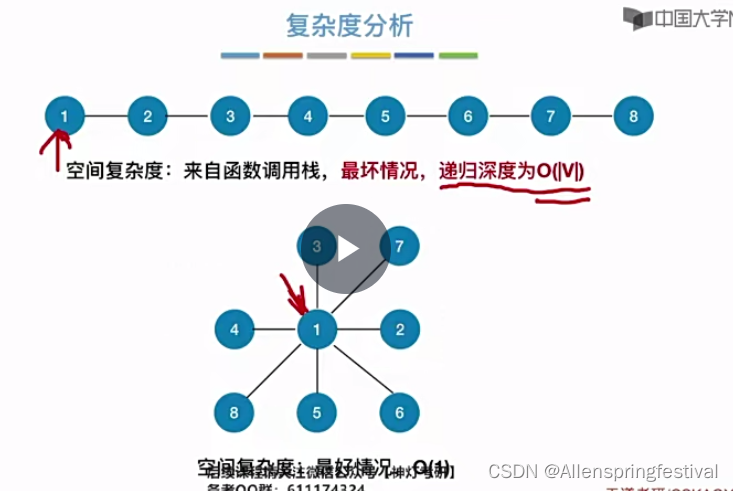
最好情况只有两层，只需要递归调用1次。O（1）

 

时间复杂度：

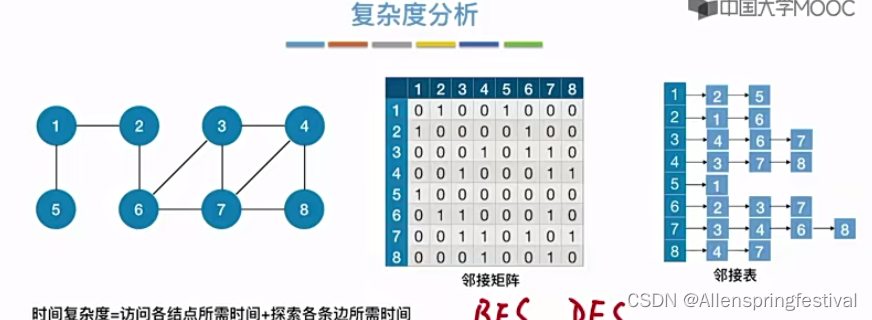
和BFS一样。

 

 

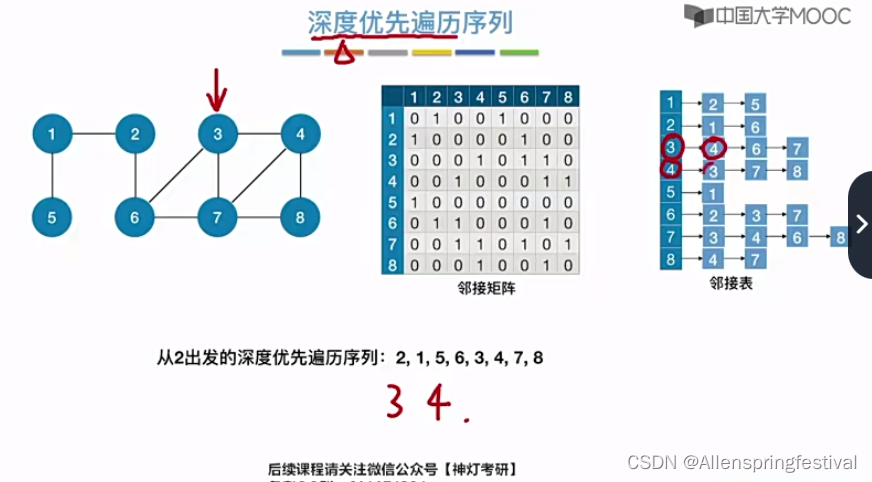
 判断深度优先遍历的序号用邻接表判断简单一些。

 

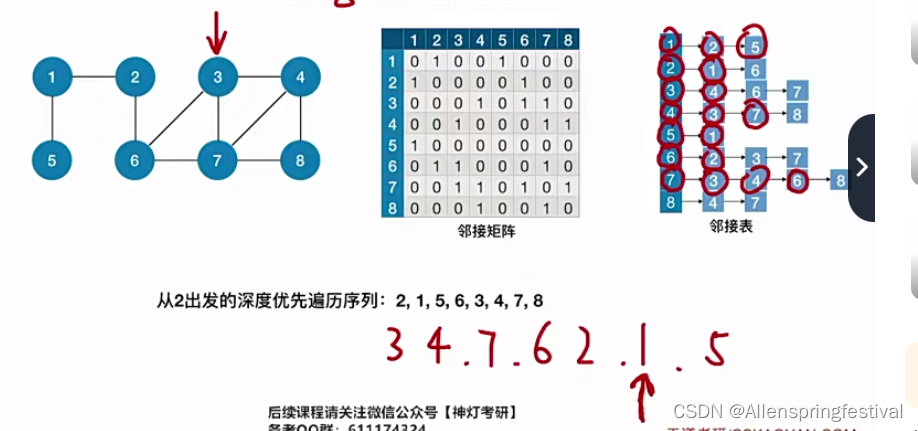
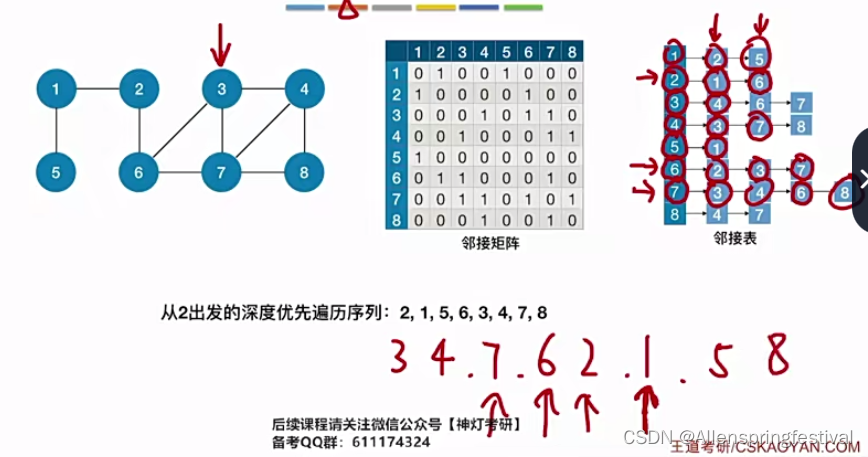
深度优先生成树：

 

深度优先生成森林：就是非联通的的图所生成的深度优先生成树。