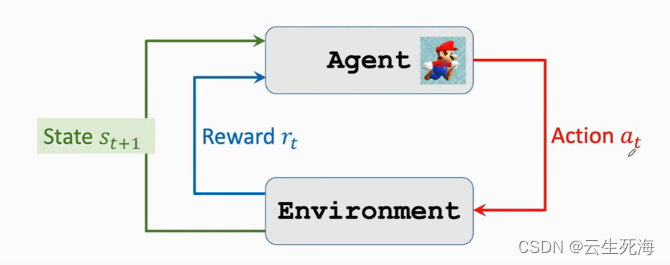
Terminologies(名词)

状态(State)
每个时刻，环境有一个状态 (state)，可以理解为对当前时刻环境的概括
状态(State) 有时也被称为观测(Observation)，因为有时智能体并不能观测到环境改变后的全部，只能观测到部分。

环境(Environment)
环境 (environment) 是与智能体进行交互的对象，可以抽象地理解为交互过程中的规则或机制。

动作(Action)
动作 (action) 是智能体基于当前状态所做出的决策。

智能体(Agent)
强化学习的主体被称为智能体 (agent)。通俗地说，由谁做动作或决策，谁就是智能体。

状态空间(State Space)
状态空间 (state space) 是指所有可能存在状态的集合，记作花体字母 S。
状态空间可以是离散的，也可以是连续的。状态空间可以是有限集合，也可以是无限可数集合。

动作空间(Action Apace)
动作空间 (action space) 是指所有可能动作的集合，记作花体字母 A
动作空间可以是离散集合或连续集合，可以是有限集合或无限集合。

策略(Policy)
**策略 (policy)**根据观测到的状态，如何做出决策，即如何从动作空间中选取一个动作。
$\pi (a|s)=P(A=a|S=s)$
强化学习的目标就是得到一个策略函数 (policy function)，也叫π函数 ( function) ，在每个时刻根据观测到的状态做出决策。策略可以是确定性的，也可以是随机性的，两种都非常有用。

奖励(Reward)
奖励 (reward) 是指在智能体执行一个动作之后，环境返回给智能体的一个数值。奖励往往由我们自己来定义，奖励定义得好坏非常影响强化学习的结果。

状态转移(State transition)
状态转移 (state transition) 是指智能体从当前 $t$时刻的状态$s$转移到下一个时刻状态为$s^{\prime }$的过程
我们用状态转移概率函数 (state transition probability function) 来描述状态转移，记作
$p_t(s^{\prime }|s,a)=P(S_{t+1}^{\prime }=s^{\prime }|S_t=s,A_t=a)$

表示这个事件的概率: 在当前状态 $s$ ，智能体执行动作$a$，环境的状态变成$s^{\prime }$

马尔可夫决策过程 (Markov decision process, MDP)

强化学习的数学基础和建模工具是马尔可夫决策过程 (Markov decision process，MDP)
一个 MDP 通常由状态空间、动作空间、状态转移函数、奖励函数、折扣因子等组成。

Return and Value

回报(Return)
回报 (return) 是从当前时刻开始到本回合结束的所有奖励的总和，所以回报也叫做累计奖励 (cumulative future reward)。

把$t$时刻的回报记作随机变量$U_t$。如果一回合游戏结束，已经观测到所有奖励，那么就把回报记作$u_t$。设本回合在时刻$n$结束。定义回报为:
$U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+...+R_n$

回报是未来获得的奖励总和，所以智能体的目标就是让回报尽量大，越大越好。强化学习的目标就是寻找一个策略，使得回报的期望最大化。这个策略称为最优策略 (optimum policy)。

折扣回报(Discounted Return)

在 MDP 中，通常使用折扣回报 (discounted return)，给未来的奖励做折扣。折扣回报的定义如下:
$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+...$
这里的$\gamma \in [0,1]$叫折扣率。对待越久远的未来，给奖励打的折扣越大。
$t$时刻当前状态$s_t$和策略函数$\pi (a|s)$选取动作$a_t$然后状态转移$p_t(s^{\prime }|s,a)=P(S_{t+1}^{\prime }=s^{\prime }|S_t=s,A_t=a)$选取新的状态$S_{t+1}^{\prime }=s^{\prime }$
奖励$R_i$只依赖于$S_i$和$A_i$

动作价值函数(Action-value function)
假设我们已经观测到状态$s_t$，而且做完决策，选中动作$a_t$。那么$U_t$中的随机性来自于$t+1$时刻起的所有的状态和动作:$S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_n,A_n$
对$U_t$关于变量$S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_n,A_n$求条件期望，得到
$Q_{\pi }(s_t,a_t)=E_{S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_n,A_n}[U_t|St=s_t,A_t=a_t]$
期望中的$S_t=s_t$和$A_t=a_t$是条件，意思是已经观测到$S_t$与 $A_t$的值。条件期望的结果$Q_{\pi }(s_t,a_t)$被称作动作价值函数 (action-value function)。
动作价值函数 $Q_{\pi }(s_t,a_t)$依赖于 $s_t$与$a_t$，而不依赖于$t+1$时刻及其之后的状态和动作，因为随机变量$S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots ,S_n,A_n$都被期望消除了。
作用：根据策略$\pi ,Q_{\pi }(s,a)$来估计当前状态$s$对于智能体选择动作$a$是否明智，得到好的效果

最优动作价值函数(Optimal action-value function)

最优动作价值函数$Q^{\ast }(s_t,a_t)$用最大化消除策略 $\pi$:
$Q^{\ast }(s_t,a_t)=ma{x}_{\pi }{Q}_{\pi }(s_t,a_t)$
$Q^{\ast }$可以对当前状态$s$对执行动作$a$做评测

状态价值函数(State-value function)

状态价值函数 (state-value function):
$V_{\pi }(s_t)=E_{A_{t\sim \pi (.|s_t)}}[Q_{\pi }(s_t,A_t)]=\sum _{a\in A}\pi (a|s_t)Q_{\pi }(s_t,a)$
公式里把动作 $A_t$作为随机变量，然后关于$A_t$ 求期望，把 $A_t$消掉。得到的状态价值函数$V_{\pi }(s_t)$ 只依赖于策略 $\pi$与当前状态 $s_t$，不依赖于动作。
状态价值函数 $V_{\pi }(s_t)$ 也是回报$U_t$ 的期望: $V_{\pi }(s_t)=E_{S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_n,A_n}[U_t|St=s_t]$ 期望消掉了 $U_t$ 依赖的随机变量 $S_{t+1},A_{t+1},S_{t+2},A_{t+2},...,S_n,A_n$状态价值越大，就意味着回报的期望越大。用状态价值可以衡量策略 $\pi$与状态$s_t$的好坏。
作用：根据策略$\pi ,V_{\pi }(s)$来估计当前状态$s$是好是坏，策略$\pi$固定，状态$s$越好$V$的值越大。
$E_s[V_{\pi }(S)]$来评估策略$\pi$的效果

如何控制智能体agent的动作？
法一 策略$\pi (a|s)$
观察状态$s_t$,随机选择动作$a_t\sim \pi (.|s_t)$
法二 动作价值函数 $Q^{\ast }(s,a)$
观察状态$s_t$,选择最大价值的动作$a_t=argma{x}_a{Q}^{\ast }(s_t,a)$