题目要求：给定一个n个元素的（升序）整型数组nums和一个目标值target，写一个函数搜索nums中的target，如果目标值存在返回下标，否则返回-1

示例

输入: nums= [-1,0,3,5,9,12]
target= 9
输出: 4
解释: 9 出现在 nums中并且下标为 4

输入: nums= [-1,0,3,5,9,12], target= 2
输出: -1
解释: 2 不存在 nums中因此返回 -1

拿到这个题目的第一想法就是逐个遍历，把数组中的每一个元素都和target进行比较，根据比较的结果按要求返回对应的值。如果数组中下标为i的元素等于target，就返回i；如果把数组全部遍历了一遍仍然没有找见target，就返回-1；

class Solution {
public:
    int search(vector<int>& nums, int target) {
        for(int i=0;i<nums.size();++i)
        {
            if(nums[i]==target)
            {
                return i;
            }
        }
        return -1 ;
    }
};

我相信大部分没有学过算法的人拿到这道题的第一想法都跟我一样，用遍历匹配的方法来做。

当然了这样能做出来，而且得到的结果肯定是正确的，但是假如数组中的元素特别多，有100万个元素，而恰好我们要找的target是第999999个，这样用遍历匹配的方法就会非常耗时。

其实我们可以改变思路让代码执行起来更简单一些，所以呢就得想另外一种方法来求解，这个方法就是二分法。 

在升序数组nums[i]中查找目标值target，可以肯定的是,对于某一特定值 i 和 target ：

• if(nums[i]==target)，则 i 就是我们需要的
• if(num[i]<target),则target只可能在 i 的右侧
• if(num[i]>target),则target只可能在 i 的左侧

基于上述基本事实，我们可以在有序数组中使用二分查找法寻找target。具体做法是，定义查找的范围是[left,right],初始查找范围是整个数组。每次取查找范围的中点mid，比较nums[mid]和target的大小，如果相等则mid为需要的下标，如果不相等则根据nums[mid]和target的大小关系将查找范围缩小一半。二分查找的条件是查找范围不为空，即left<=right。如果target在数组中，二分查找就可以找到target，并返回target在数组中的下标。如果target不在数组中，就返回-1。

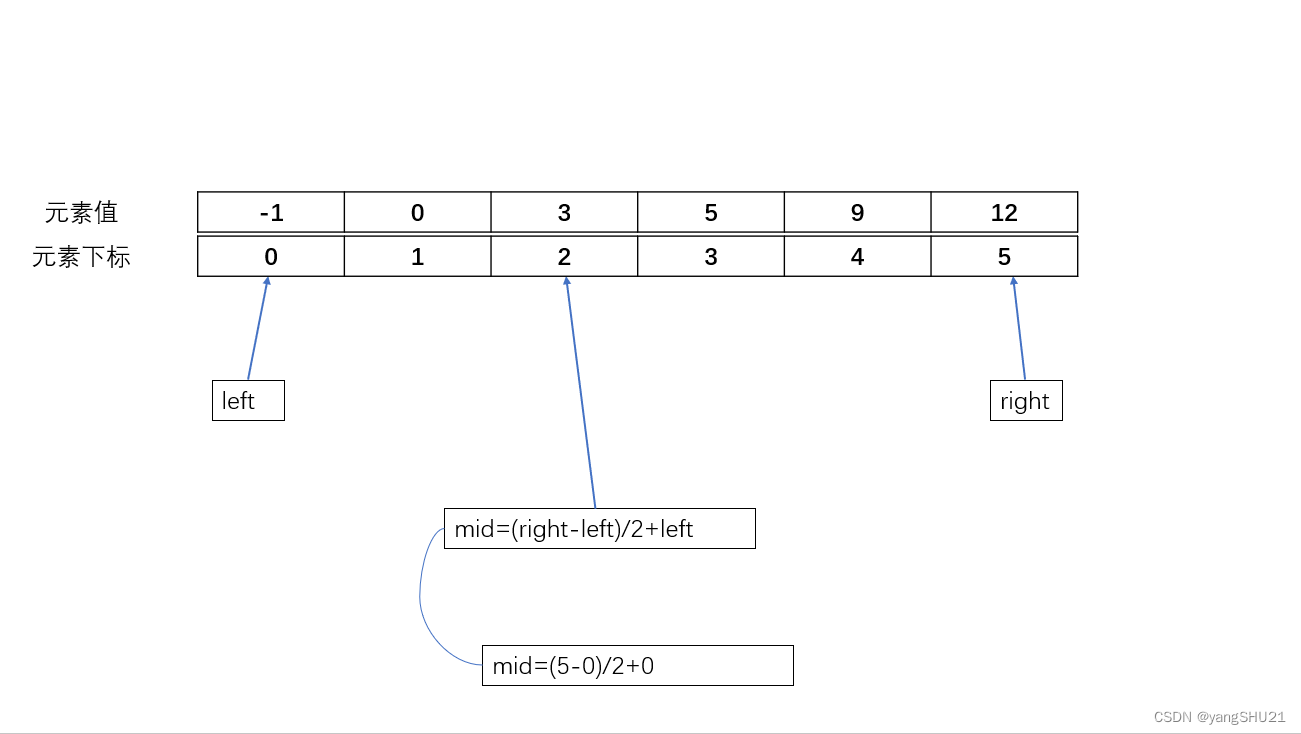
具体的代码如下

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=(right-left)/2+left;
            if(nums[mid]==target)
            {
                return mid;
            }
            else if(nums[mid]>target)
            {
                right=mid-1;
            }
            else
            {
                left=mid+1;
            }
        }
        return -1;
    }
};

我们把它放在vs里面测试一下

#include<iostream>
#include<vector>
using namespace std;

int search(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
        while (left <= right)
        {
            int mid = (right - left) / 2 + left;
            if (nums[mid] == target)
            {
                return mid;
            }
            else if (nums[mid] > target)
            {
                right = mid - 1;
            }
            else
            {
                left = mid + 1;
            }
        }
        return -1;
 }

int main()
{
    vector<int> vec{ 1,4,5,7,11,14,18 };
    cout << "vec: ";
    for (auto c : vec)
    {
        cout << c << " ";
    }
    cout << endl;
    /*int tar = 5;*/
    int tar = 2;
    int i=search(vec, tar);
    if (i >= 0)
        cout << tar<<" index is " << i << endl;
    else
        cout << tar<<" not found" << endl;
}

分别测试两个数，结果如下：