红黑树是一种自平衡二叉查找树,具有良好的时间复杂度和空间复杂度,被广泛应用于计算机科学领域中,如操作系统、编译器、数据库等。在实际应用中,红黑树主要用于实现高效的查找和排序,如 Linux 内核中的进程调度和空闲内存的管理,C++ STL库中的 map 和 set 容器等均使用了红黑树实现。下面将介绍红黑树的特点、基本概念、插入操作、删除操作以及与平衡二叉树和二叉搜索树的区别和联系,同时提供C++代码实现。
本文目录
- 1. 红黑树的特点(性质)
- 2. 基本概念
- 3. 插入操作
- 4. 删除操作
- 5. 与平衡二叉树和二叉搜索树的区别和联系
- 6. C++ 代码实现
1. 红黑树的特点(性质)
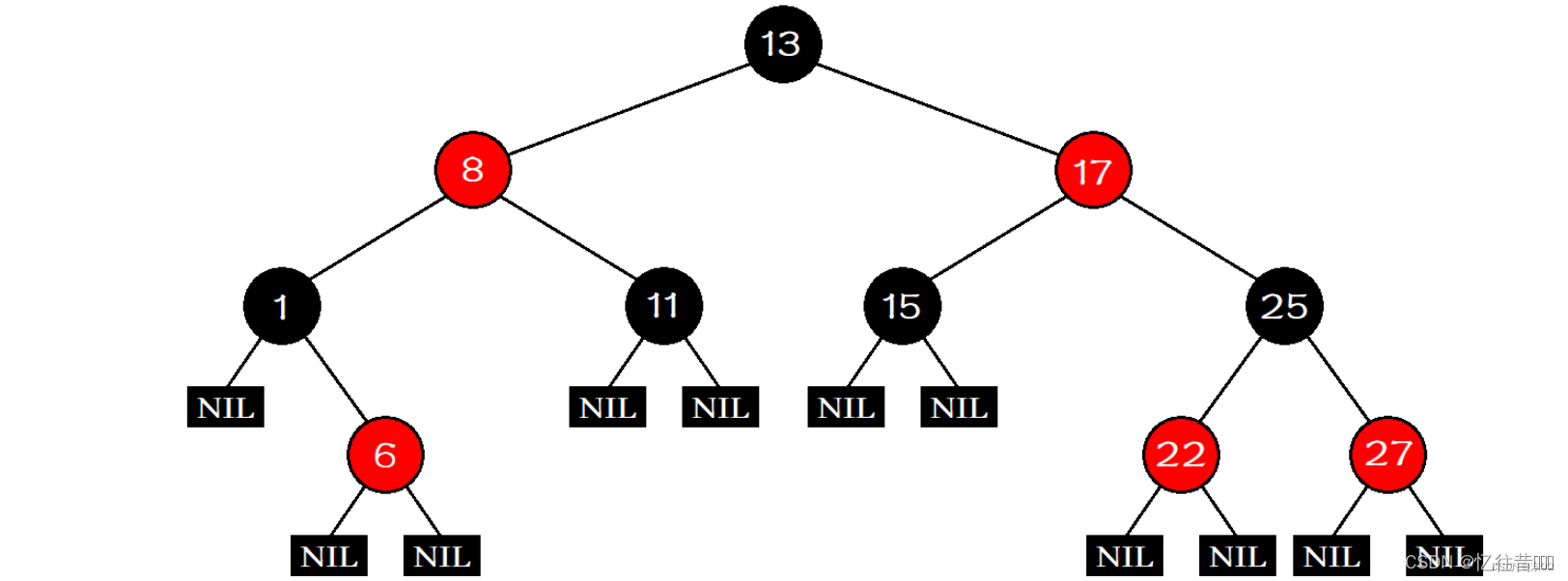
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL节点);
- 每个红色节点的两个子节点都是黑色的;
- 任意一条从根节点到叶子节点的路径上,不能出现连续的两个红色节点;
- 任意节点到其每个叶子节点的所有路径包含相同数目的黑色节点。
红黑树保证了树的高度(即从根节点到叶子节点的最长路径)最长不超过最短路径的两倍,因而保证了其查找、插入、删除操作的时间复杂度都可以稳定地达到 O(log n) 的级别。
2. 基本概念
- 黑色节点(B):颜色为黑色的节点。
- 红色节点(R):颜色为红色的节点。
- 空节点(NIL):通常用于代表叶子节点,其颜色为黑色。
- 黑高度(bh):从某个节点到其叶子节点的任意一条路径上的黑色节点数目,空节点的黑高度为0。
- 平衡:红黑树的节点个数的增减都不会使树的高度增加很多。
3. 插入操作
红黑树的插入操作分为以下几步:
- 将新节点插入到红黑树中,颜色为红色。
- 如果插入节点的父节点为黑色,则插入完成。
- 如果插入节点的父节点为红色,则需要进行调整,以恢复红黑树的平衡。
(a)将插入节点的父节点称为节点P,节点P的父节点称为节点G,节点P的兄弟节点称为节点U;
(b)如果节点G是树的根节点,则置节点G为黑色;
(c)如果节点U是红色,则将节点P和节点U都置为黑色,将节点G置为红色,再以节点G为当前节点进行平衡处理;
(d)如果节点U是黑色,且插入节点为节点P的右节点,即P为G的左孩子,则以P为当前节点进行左旋;
(e)如果节点U是黑色,且插入节点为节点P的左节点,即P为G的右孩子,则以P的左子节点为支点进行右旋;
(f)将节点P置为黑色,将节点G置为红色,以节点G为当前节点进行平衡处理。
4. 删除操作
红黑树的删除操作分为以下几步:
- 从红黑树中删除要删除的节点。
- 如果删除节点的颜色为红色,则直接删除即可,不需要进行调整操作,红黑树的平衡依然成立。
- 如果删除节点的颜色为黑色,则需要进行调整,以恢复红黑树的平衡。
(a)如果删除节点的兄弟节点W是红色的,则以删除节点的父节点P为支点进行左旋或右旋,将W置为黑色,P置为红色,再以W的原来的兄弟节点为新的W节点进行处理;
(b)如果删除节点的兄弟节点W是黑色的,则需要判断W节点的两个子节点的颜色:如果W的两个子节点都是黑色的,则将W节点置为红色,并以P节点为新的删除节点进行平衡处理;如果W的左节点是红色的,右节点是黑色的,则以W节点为支点进行右旋,将W的左节点置为黑色,W置为红色,再以P节点为新的删除节点进行平衡处理;如果W的右节点是红色的,则以P节点为支点进行左旋,将W节点置为红色,W的右节点置为黑色,再以P节点的父节点为新的删除节点进行平衡处理。
5. 与平衡二叉树和二叉搜索树的区别和联系
红黑树、平衡二叉树和二叉搜索树都是非常常见并且重要的数据结构,它们之间有如下的区别和联系:
区别:
- 二叉搜索树(BST):左子树的所有节点值小于根节点,右子树的所有节点值大于根节点,且左右子树也都是 BST。
- 平衡二叉树:是一种特殊的 BST,即使在最坏情况下,其高度近似于 log N,从而使得查找和删除等操作的时间复杂度可控,通常通过平衡因子进行平衡(如 AVL 树)。
- 红黑树:是一种二叉搜索树,通过插入、删除等操作来保证树的平衡性,通过约束节点为红或黑色的颜色,从而保证了其近似于平衡。
联系:
- 平衡二叉树和红黑树都是为了保证二叉搜索树的平衡性而引入的改进方法,目的是尽可能保证树的高度较小,以保证时间复杂度的可控性。
- 红黑树可以看做是一种弱化的平衡二叉树,也就是说,红黑树的平衡条件比 AVL 树等要宽松一些,这就使得其在实际应用中更加灵活。
因为其平均时间复杂度为 O(log N),二叉搜索树、平衡二叉树和红黑树都被广泛应用于搜索、排序、存储和索引等领域。需要根据具体的应用场景和实际情况选择不同的数据结构。
6. C++ 代码实现
下面是使用 C++ 语言实现红黑树的代码,包括节点的定义、查找、插入和删除等操作。
enum Color {RED, BLACK};
template <typename Key, typename Value>
class RBTree {
private:
struct Node {
Key key;
Value value;
Color color;
Node *left, *right, *parent;
Node(Key key, Value value)
: key(key), value(value), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};
Node* root;
// 查找节点
Node* findNode(Key key, Node* node) {
if (node == nullptr || node->key == key) {
return node;
} else if (node->key < key) {
return findNode(key, node->right);
} else {
return findNode(key, node->left);
}
}
// 左旋
void leftRotate(Node* x) {
Node *y = x->right;
x->right = y->left;
if (y->left != nullptr) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
// 右旋
void rightRotate(Node* x) {
Node *y = x->left;
x->left = y->right;
if (y->right != nullptr) {
y->right->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->right = x;
x->parent = y;
}
// 插入节点
void insertNode(Key key, Value value) {
Node *z = new Node(key, value);
Node *y = nullptr;
Node *x = root;
while (x != nullptr) {
y = x;
if (z->key < x->key) {
x = x->left;
} else {
x = x->right;
}
}
z->parent = y;
if (y == nullptr) {
root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = nullptr;
z->right = nullptr;
z->color = RED;
insertFixup(z);
}
// 插入修复
void insertFixup(Node *z) {
while (z->parent != nullptr && z->parent->color == RED) {
if (z->parent == z->parent->parent->left) {
Node *y = z->parent->parent->right;
if (y != nullptr && y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
} else {
if (z == z->parent->right) {
z = z->parent;
leftRotate(z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rightRotate(z->parent->parent);
}
} else {
Node *y = z->parent->parent->left;
if (y != nullptr && y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
rightRotate(z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
leftRotate(z->parent->parent);
}
}
}
root->color = BLACK;
}
// 删除节点
void deleteNode(Key key) {
Node *z = findNode(key, root);
if (z == nullptr) {
return;
}
Node *y = nullptr;
if (z->left == nullptr || z->right == nullptr) {
y = z;
} else {
y = findNode(key + 1, z->right);
}
Node *x = nullptr;
if (y->left != nullptr) {
x = y->left;
} else {
x = y->right;
}
if (x != nullptr) {
x->parent = y->parent;
}
if (y->parent == nullptr) {
root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
if (y != z) {
z->key = y->key;
z->value = y->value;
}
if (y->color == BLACK) {
deleteFixup(x, y->parent);
}
delete y;
}
// 删除修复
void deleteFixup(Node *x, Node *p) {