前言

最近想学习一下并网逆变器，需要用到PR控制，全网找遍了许多学习资料，终于掌握的差不多了，在此做个记录，以及个人对PR(Proportional Resonant)控制的理解。

基本知识

PR控制的传递函数形式为
$H(s)=Kp+\frac{2Krs}{s^2+\omega_o^2}$ 。
利用matlab绘制一下该传递函数的幅频响应，是在谐振频率 $\omega=\omega_o$ 的频率点增益无穷大，且没有相位滞后。
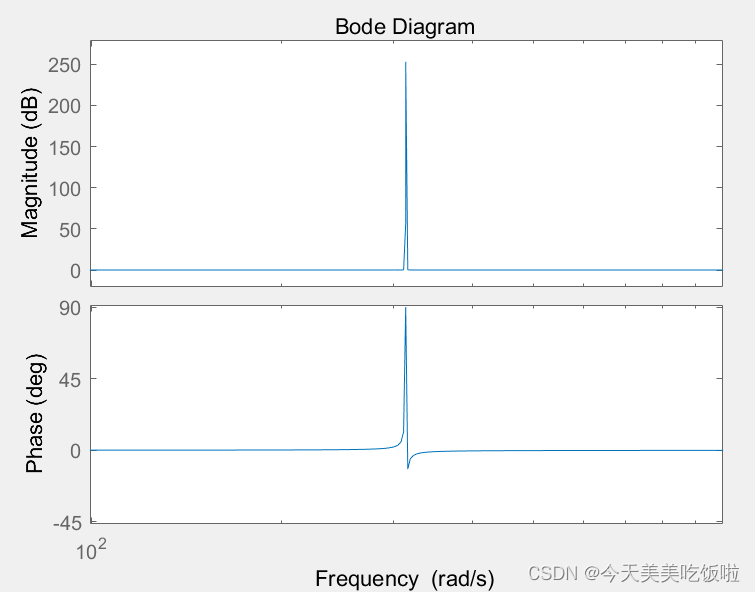
在这里插入图片描述

根据PR控制器上述的特性，我们可以设计谐振频率等于电网的角频率，使电网基波信息增益无穷大而其他频段增益下，从而应用在交流电路的控制中。

至于为什么不用传统的PID控制，其原因是PID控制器对于交流信号的控制性能差，对直流信号的跟踪性能好。因此DCDC变换中多采用PID控制，而在交流中也可以通过DQ坐标变换，将需要控制的交流信号变换为直流信号，再用直流控制器PID就可以实现很好的控制效果了。

总而言之，PID是直流信号控制器；PR是交流控制器。

实际使用

实际应用中，由于电网频率不会严格的等于50Hz，难免存在波动，因此前文提到的PR控制器在电网频率稍微偏离50Hz，性能大幅变差。为增加控制的鲁棒性，增加截止频率 $\omega_c$ ，改写传递函数为
$H(s)=Kp+\frac{2Kr\omega_cs}{s^2+2Krw_cs+\omega_o^2}$

修改后的PR控制器，亦称为准比例谐振控制Quasis Proportional Resonant，在谐振频率附近的小范围内，仍然具有高增益，因此能适用电网频率波动的情况。

至此，我们发现应用准谐振控制时需要整定3个参数，Kp，Kr，wc。先回顾一下PID的三个参数。

P因子，决定响应速度；
I因子，决定稳态误差；
D因子，决定抗扰能力。

而通常在电力电子中多用PI控制，电力传动有PI也有PD。PI控制电机无静差调速，可用于舵机消除抖动。

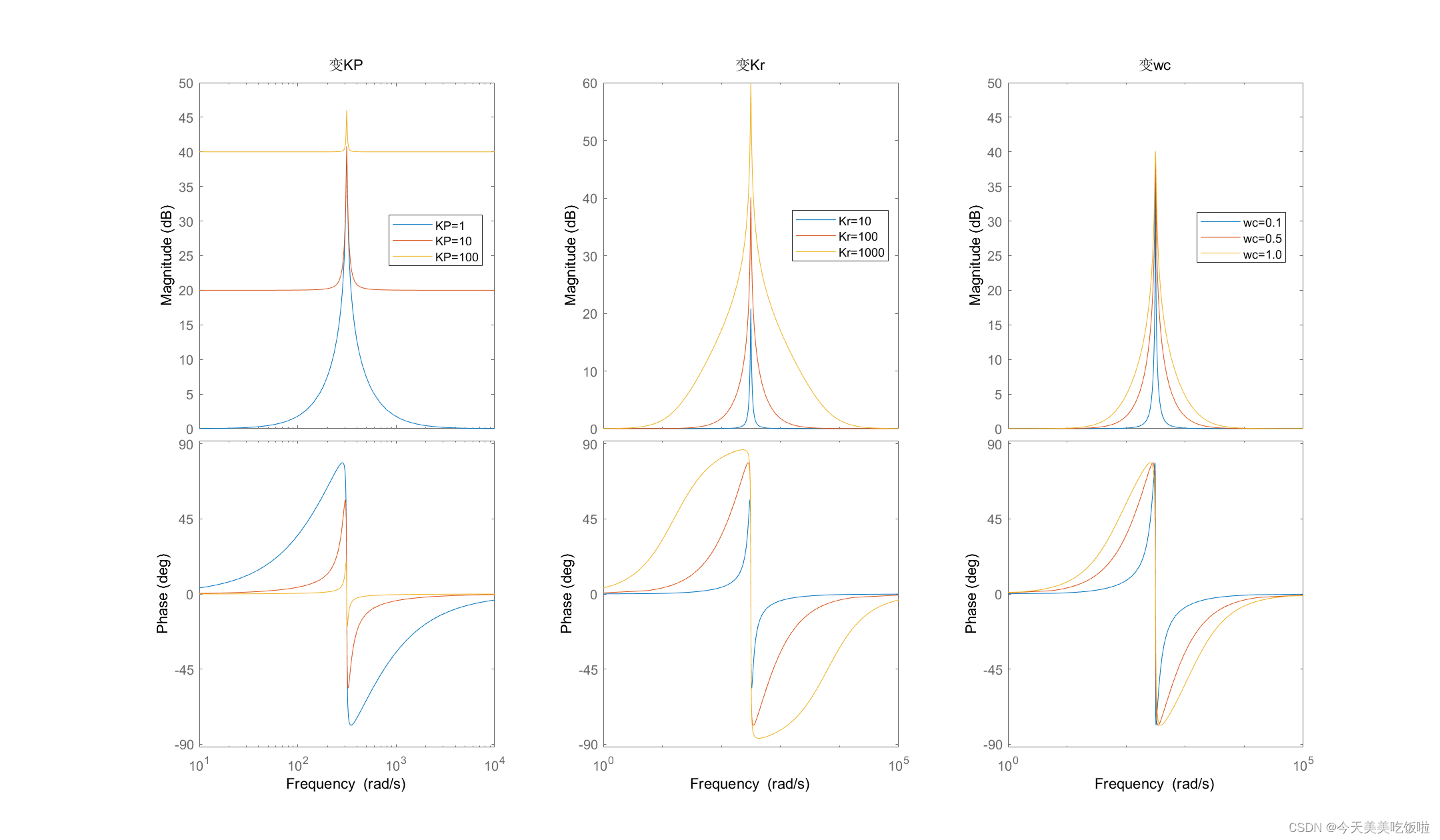
为了观察准比例谐振控制器中三个参数的影响，同样用MATLAB绘制bode图，控制变量法来看。
在这里插入图片描述

figure()
subplot(1,3,1)
Kp=1;Kr=100;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=10;Kr=100;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=100;Kr=100;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
legend('KP=1','KP=10','KP=100');title('变KP')
subplot(1,3,2)
Kp=1;Kr=10;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=1;Kr=100;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=1;Kr=1000;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
legend('Kr=10','Kr=100','Kr=1000');title('变Kr')
subplot(1,3,3)
Kp=1;Kr=100;wc=0.1*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=1;Kr=100;wc=0.5*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
Kp=1;Kr=100;wc=1*2*pi;wo=100*pi;PRs1=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);bode(PRs1);hold on;
legend('wc=0.1','wc=0.5','wc=1.0');title('变wc')

由bode图可知，Kp越大，其他低频段和高频段的增益越大；Kr越大，谐振点的增益越大，但附近周围频带的增益也相应有所增大；wc越大，周围频带的增益也相应有所增大。

而参数wc可以任意取 $2\pi\times 0.1$ 、 $2\pi\times 0.5$ 、 $2\pi\times 1$ ，真正需要整定的参数也就只有Kp和Kr了。

单相离网逆变器

离网逆变器是把DC逆变出来的AC电直接使用，输出接负载，控制对象是输出电压，力争低THD，幅值可控。

控制结构框图
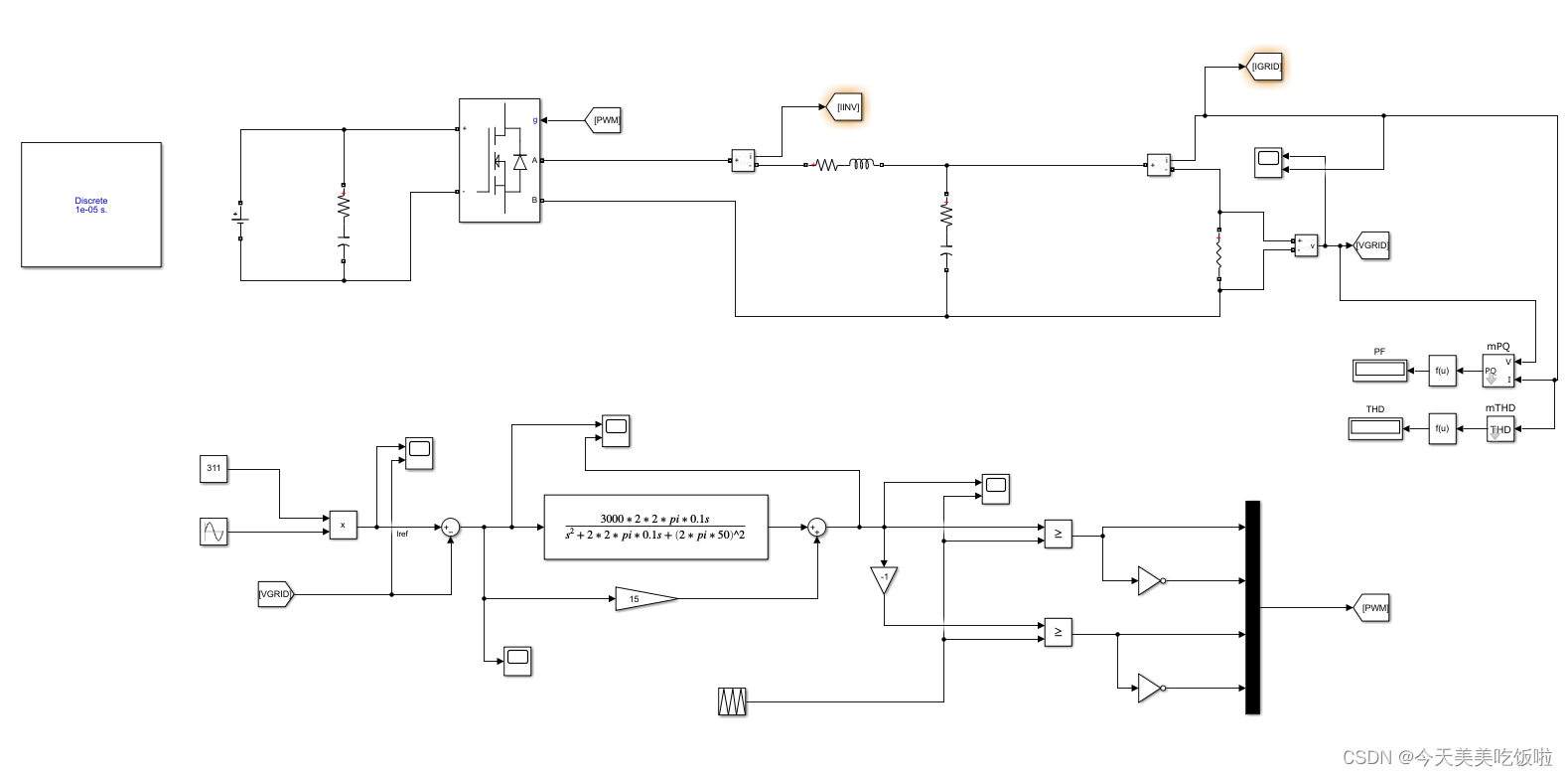
在这里插入图片描述
资源链接
基于PR控制的单相离网逆变器

单相并网逆变器

并网逆变器是把DC逆变出来的AC电送入另一个交流系统，输出端接电网，控制对象是输出电流，力争低THD，幅值可控，且与电网电压同相位。

控制结构框图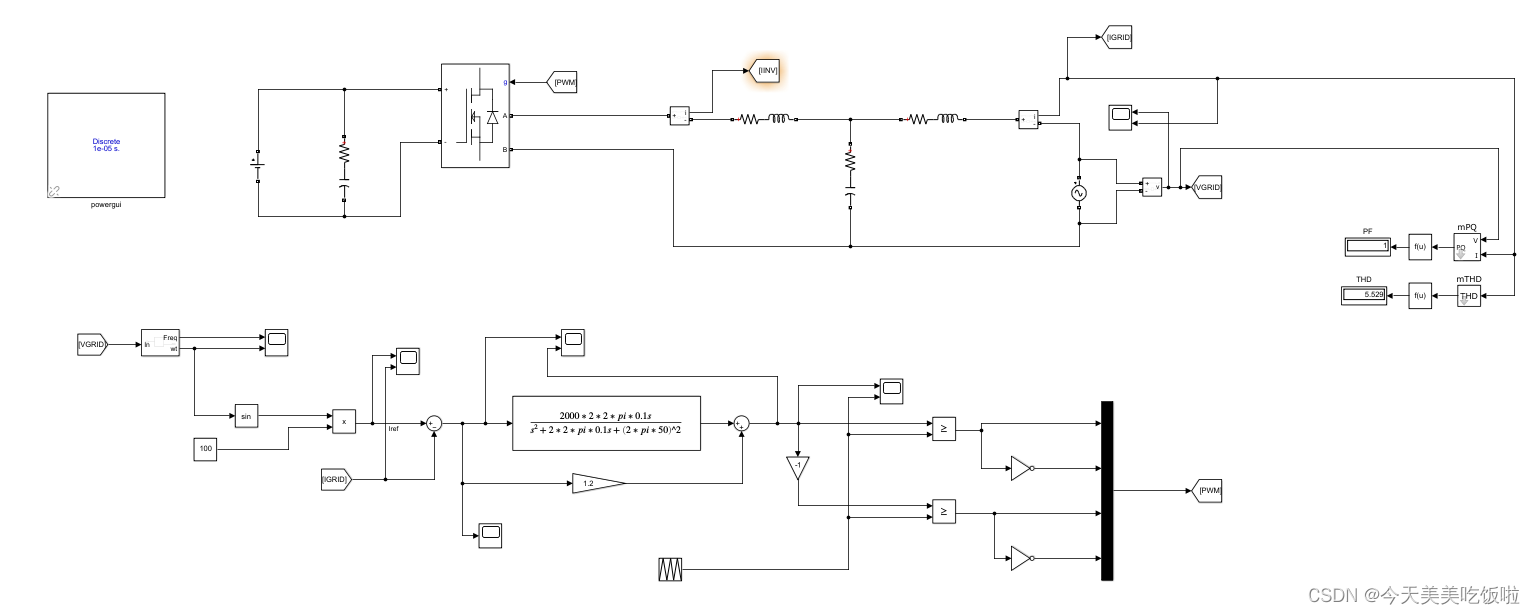在这里插入图片描述
资源链接

基于PR控制的单相并网逆变器控制

PR控制器离散化

基本知识

目前而言，同一种控制方式有3种表达形式

时域，有连续时域和离散时域之分
复频域，又称s域
z域

在大学之前的学习一直都是时域下的，也是最简单最容易理解的。大学期间接触的拉氏变换是由连续时域到复频域的变换，z变换是离散时域到z域的变换。

在连续时域下，描述不同时间点的方程称为微分方程。
在离散时域下，描述不同时间点的方程称为差分方程。

本人目前尚未学习到s域和z域之间的转换，好在有众多前人的研究基础。
在这里插入图片描述
方法很多，选哪一个种呢？在TI写的数字锁相环算法库中有说明文档详细推导各个参数的计算，其中就涉及到连续传递函数离散化的问题，TI采用的Tustin。简单期间我们也选Tustin方法了。

MATLAB也提供了传递函数离散化的内置函数c2d。

Ts=1/25000;
Kp=1;
Kr=100;
wc=0.5*2*pi;
wo=100*pi;
c=Kp+tf([2*Kr*wc,0],[1 2*wc wo*wo]);
d=c2d(c,Ts,'tustin');

但是好像不能用MALTAB计算出准谐振的离散化结果，索性直接带入化简得了。

过程略，结果如下。
在这里插入图片描述
在当初学习的时候一直在思考离散化里面的T到底是什么。我的理解就是，相邻两次以离散化的方式实现连续传递函数的时间间隔，即T。在DSP中的控制一般写在中断中，那么对应的T即中断时间间隔。而在Simulink仿真中，Powergui和模型设置这两个地方都能设置步长，到底哪个才是真正的呢？目前没有想明白，若想要验证的话设置为相同的步长即可。

当时学习的时候也有一个疑问，为什么在学习PID控制器的时候没有所谓的离散化步骤。怎么就直接把PID的C语言实现给写出来了呢？是因为PID的连续时域表达式简单，很容易就能推导出离散时域表达式，用的是微积分的思想。而在学习PR控制器的时候，是先有他的传递函数，即s域表达式，可以直接从s域到z域变换。

那实现数字一阶滤波器的时候呢？也是先根据模拟RC电路推导传递函数，再变到连续时域，离散时域。那稍微复杂一点的二阶甚至高阶滤波器呢，就是直接从s域到z域到离散时域的。

总之，当我们用数字方式实现控制时，根本目的是得到他的离散时域表达式。

DSP实现

有了Z域下的表达式，可以直接得到离散时域表达式，即差分方程。

以二阶为例， $\frac{Y(z)}{X(z)}=\frac{A_0+A_1z^{-1}+A_2z^{-2}}{B_0+B_1z^{-1}+B_2z^{-2}}$ 。
则离散时域表达式为 $B_0y[n]+B_1y[n-1]+B_2y[n-2]=A_0x[n]+A_1x[n-1]+A_2x[n-2]$ 。

因此可以根据前面推导的PR控制器的在Z域下的通用表达式，写出它的通用离散时域表达式。

/*
 * myPR.c
 *
 *  Created on: 2023年4月25日
 *      Author: EnglishName
 */

#include <myAPP/myPR/myPR.h>

PR pr_v_ac = { 0 };
PR pr_i_ac = { 0 };

void PR_init(PR *p,float32 Kp,float32 Kr,float32 Ts,float32 wc, float32 wo)
{
    float temp = 0;
    p->Ts=Ts;
    p->Kp=Kp;
    p->Kr=Kr;
    p->wc=wc;
    p->wo=wo;
    temp = 4 / p->Ts / p->Ts + 4 * p->wc / p->Ts + p->wo * p->wo;

    p->B0 = (4 * p->Kp / p->Ts / p->Ts + 4 * p->wc * (p->Kp + p->Kr) / p->Ts
            + p->Kp * p->wo * p->wo) / temp;
    p->B1 = (-8 * p->Kp / p->Ts / p->Ts + 2 * p->Kp * p->wo * p->wo) / temp;
    p->B2 = (4 * p->Kp / p->Ts / p->Ts - 4 * p->wc / p->Ts * (p->Kp + p->Kr)
            + p->Kp * p->wo * p->wo) / temp;
    p->A1 = (-8 / p->Ts / p->Ts + 2 * p->wo * p->wo) / temp;
    p->A2 = (4 / p->Ts / p->Ts - 4 * p->wc / p->Ts + p->wo * p->wo) / temp;
    /*PRpr;
     * 差分方程
     * y[n]+A1[n-1]+A2[n-2]=B0x[n]+B1x[n-1]+B2[n-2]
     */
}

void PR_calc(PR *p)
{
    p->vo = -p->A1 * p->vo_1 - p->A2 * p->vo_2 + p->B0 * p->vi + p->B1 * p->vi_1
            + p->B2 * p->vi_2;

    // update and store
    p->vo_2=p->vo_1;
    p->vo_1 = p->vo;
    p->vi_2 = p->vi_1;
    p->vi_1 = p->vi;
}

/*
 * myPR.h
 *
 *  Created on: 2023年4月25日
 *      Author: EnglishName
 */

#ifndef MYAPP_MYPR_MYPR_H_
#define MYAPP_MYPR_MYPR_H_

#include "F28x_Project.h"

typedef struct
{
    float Kp;
    float Kr;
    float wo;
    float wc;
    float Ts;
    float A0, A1, A2, B0, B1, B2;
    float vo, vo_1, vo_2;
    float vi, vi_1, vi_2;
} PR;

extern PR pr_v_ac;
extern PR pr_i_ac;

void PR_init(PR *p, float32 Kp, float32 Kr, float32 Ts, float32 wc, float32 wo);
void PR_calc(PR *p);

#endif /* MYAPP_MYPR_MYPR_H_ */