目录

一、树存储结构

1.1双亲表示法

 1.2孩子表示法

*1.3孩子兄弟表示法

* 二、树，森林、二叉树之间的转化

 三、树和森林的遍历

3.1树

*3.1.1先根遍历

*3.1.2后根遍历

*3.1.3层次遍历

 3.2森林

* 3.2.1先序遍历

 *3.2.2中序遍历

 *等同关系

四、哈夫曼树和哈夫曼编码

4.1哈夫曼树定义

*4.2哈夫曼树构造

*4.3哈夫曼编码

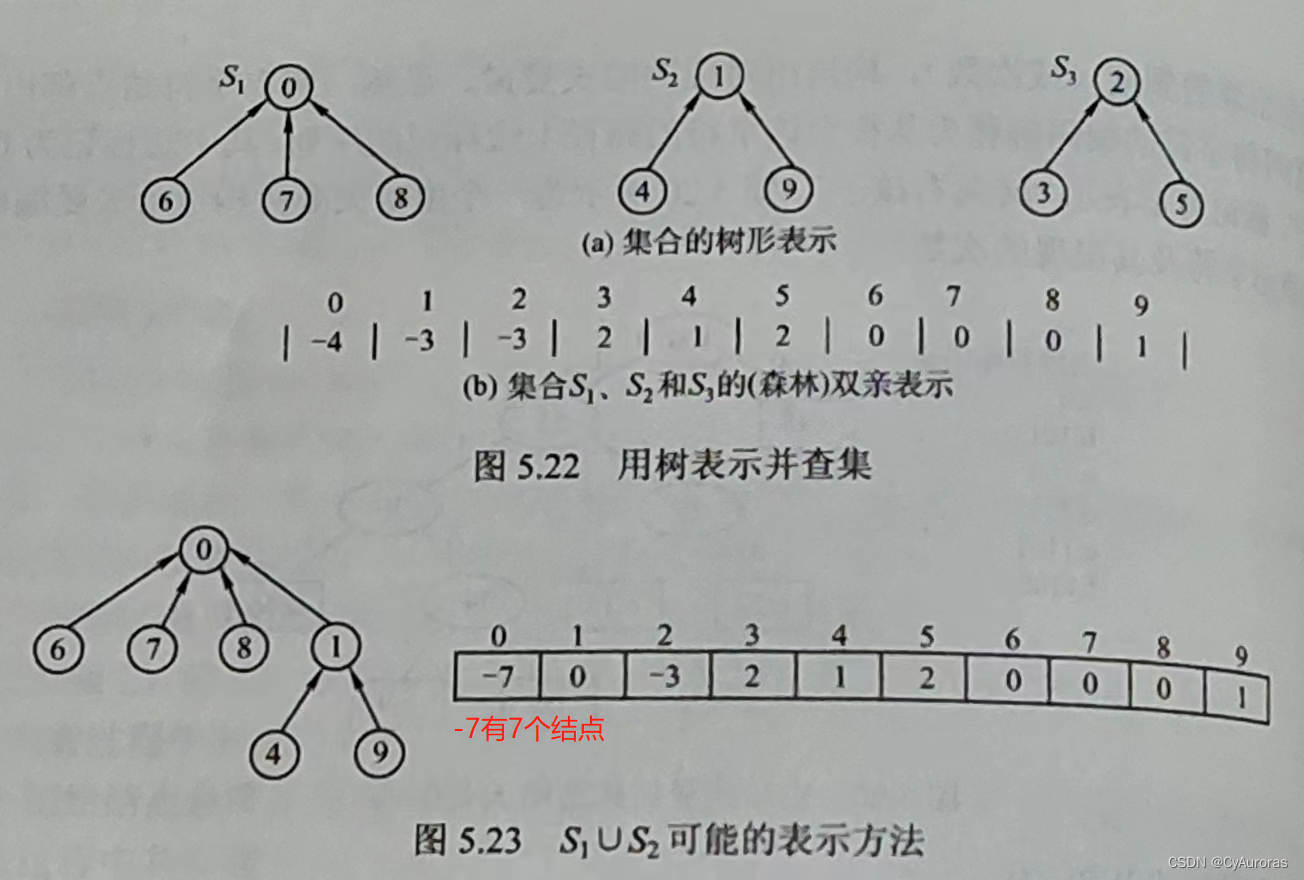
 五、并查集

*5.1 并查集里题​编辑

---

一、树存储结构

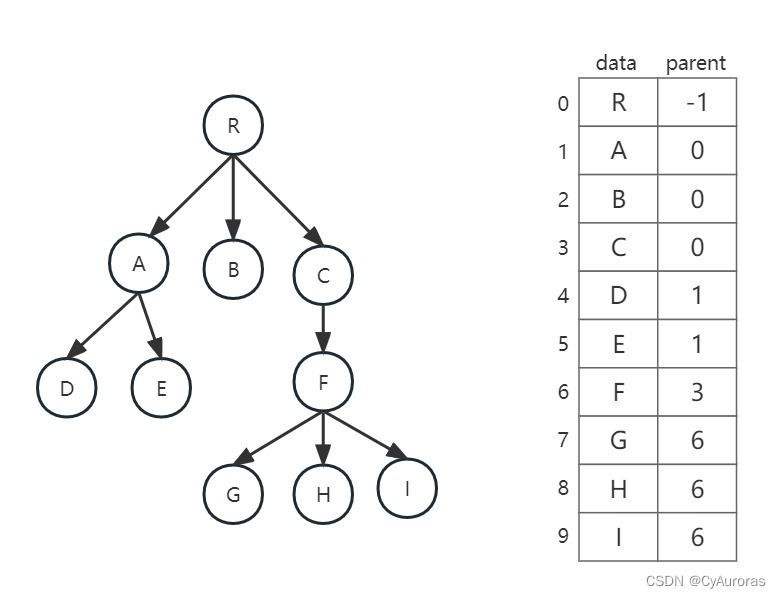
1.1双亲表示法

采用连续的空间来存储每个结点，每个结点设一个伪指针，指示双亲结点(父结点)在数组的位置

#define MAX_TREE_SIZE 100
typedef struct{
    int data;                        //数据元素
    int parent;                      //父结点位置
}PTNode;
typedef struct{
    PTNode nodes[MAX_TREE_SIZE];     //结点
    int n;                           //结点树
}

 1.2孩子表示法

struct CTNode{
    int child;            //孩子结点在数组的位置
    struct CTNode *next;  //下一个孩子
}
typedef struct{
    int data;
    struct CTNode *firstChild;   //第一个孩子
}CTBob;
typedef struct{
    CTBox nodes[MAX_TREE_SIZE];
    int n;
}CTree;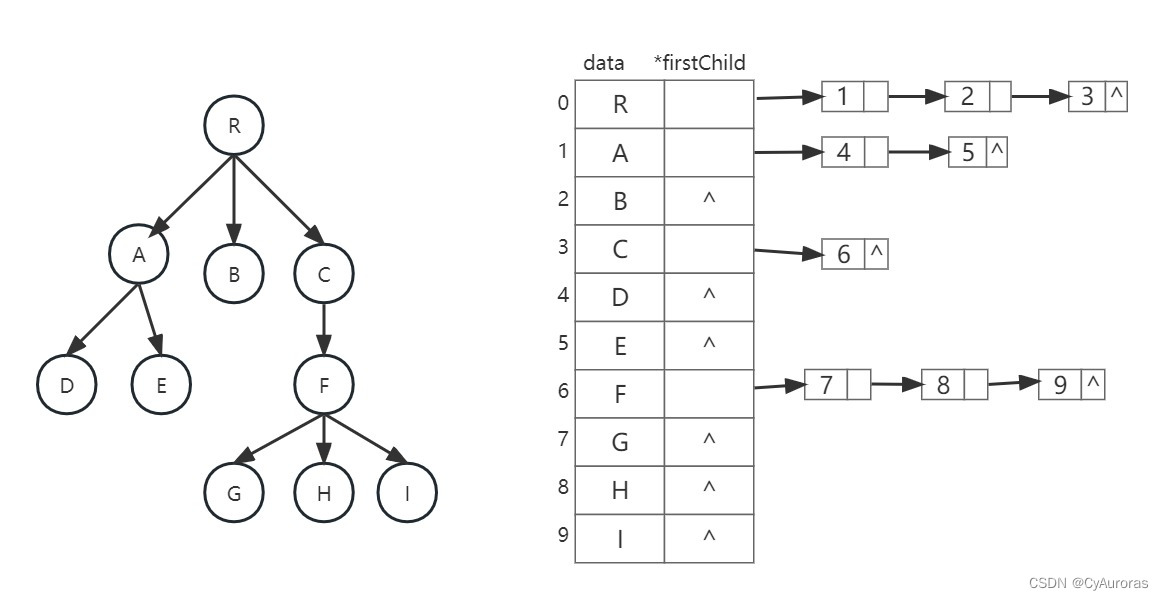

*1.3孩子兄弟表示法

typedef struct CSNode{
    int data;
    struct CSNode *firstchild,*nextsibling;    //第一个孩子和右兄弟指针
}CSNode,*CSTree;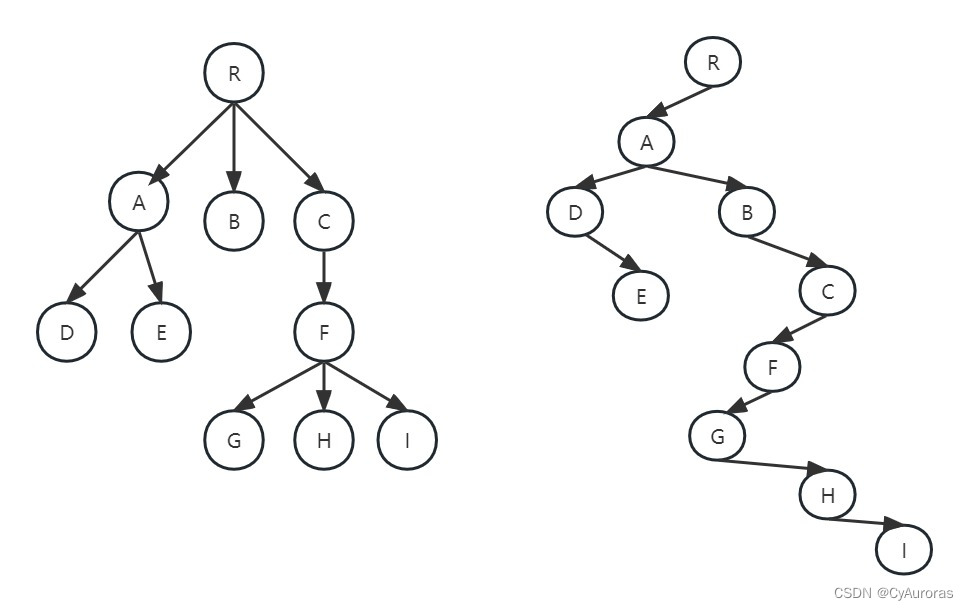

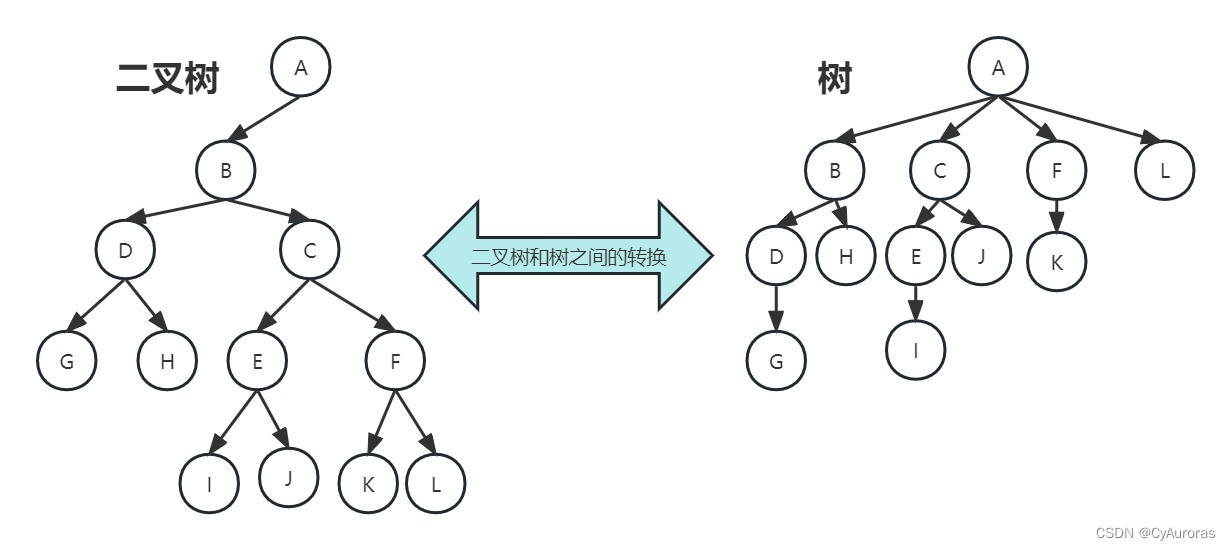
* 二、树，森林、二叉树之间的转化

 

 三、树和森林的遍历

3.1树

*3.1.1先根遍历

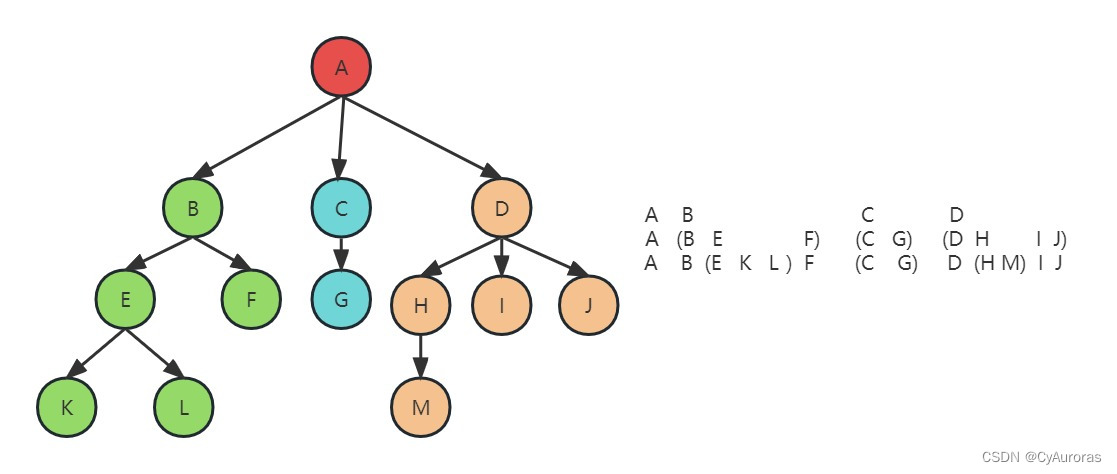
和转换成二叉树的先根遍历序列相同

void PreOrder(TreeNode *R){
    if(R!=NULL){
        visit(R);
        while(R下一个子树)
            PreOrder(T);
    }
}

*3.1.2后根遍历

根上述原理相同

void PreOrder(TreeNode *R){
    if(R!=NULL){
        while(R下一个子树)
            PreOrder(T);
        visit(R);
    }
}

*3.1.3层次遍历

根二叉树一样，队列辅助

 3.2森林

* 3.2.1先序遍历

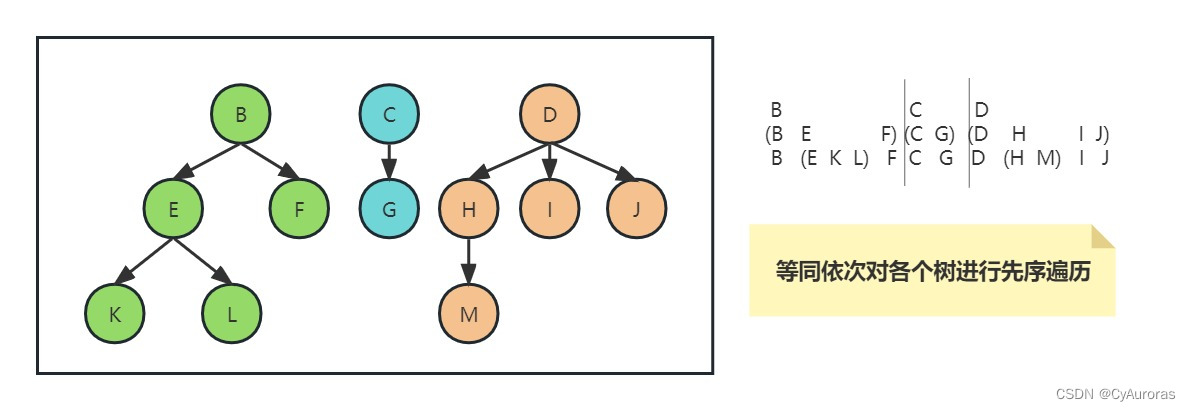
 *3.2.2中序遍历

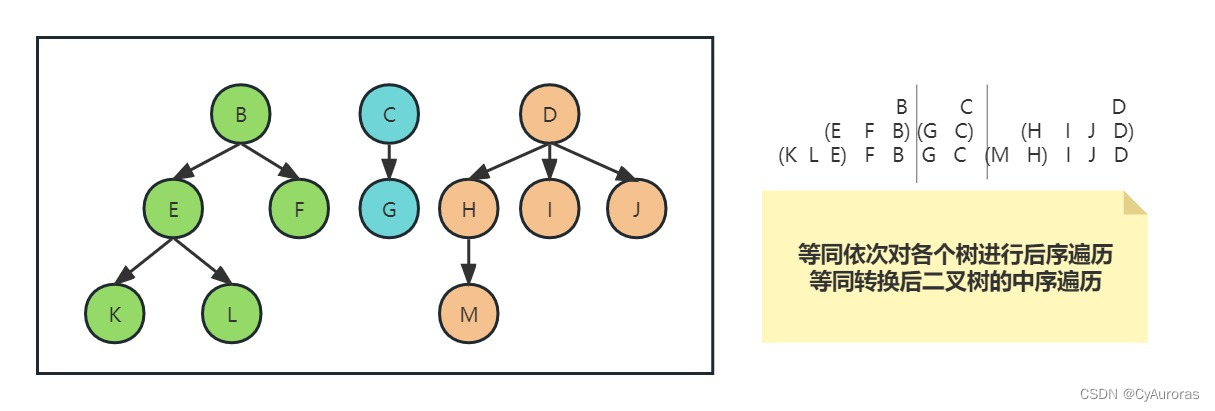
 *等同关系

树	二叉树	森林
先序	先序	先序
后续	中序	中序

四、哈夫曼树和哈夫曼编码

4.1哈夫曼树定义

从根结点到任意结点的路径长度于该结点上的权值乘积，称该结点带权路径长度，

记,其中是第i个叶结点所带的权值，是叶结点到根结点的路径长度

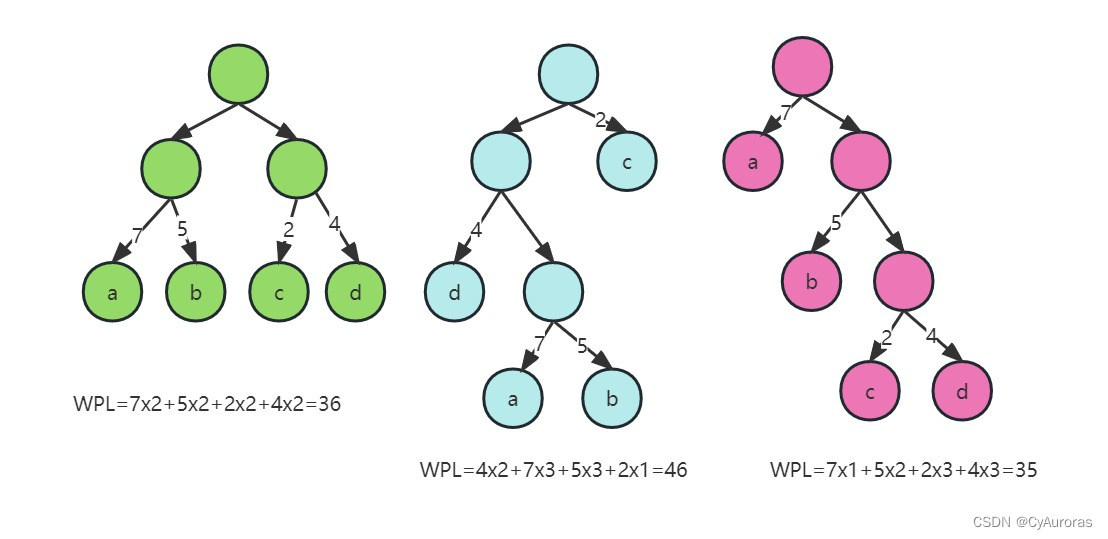
 WPL=36最小，所以是哈夫曼树

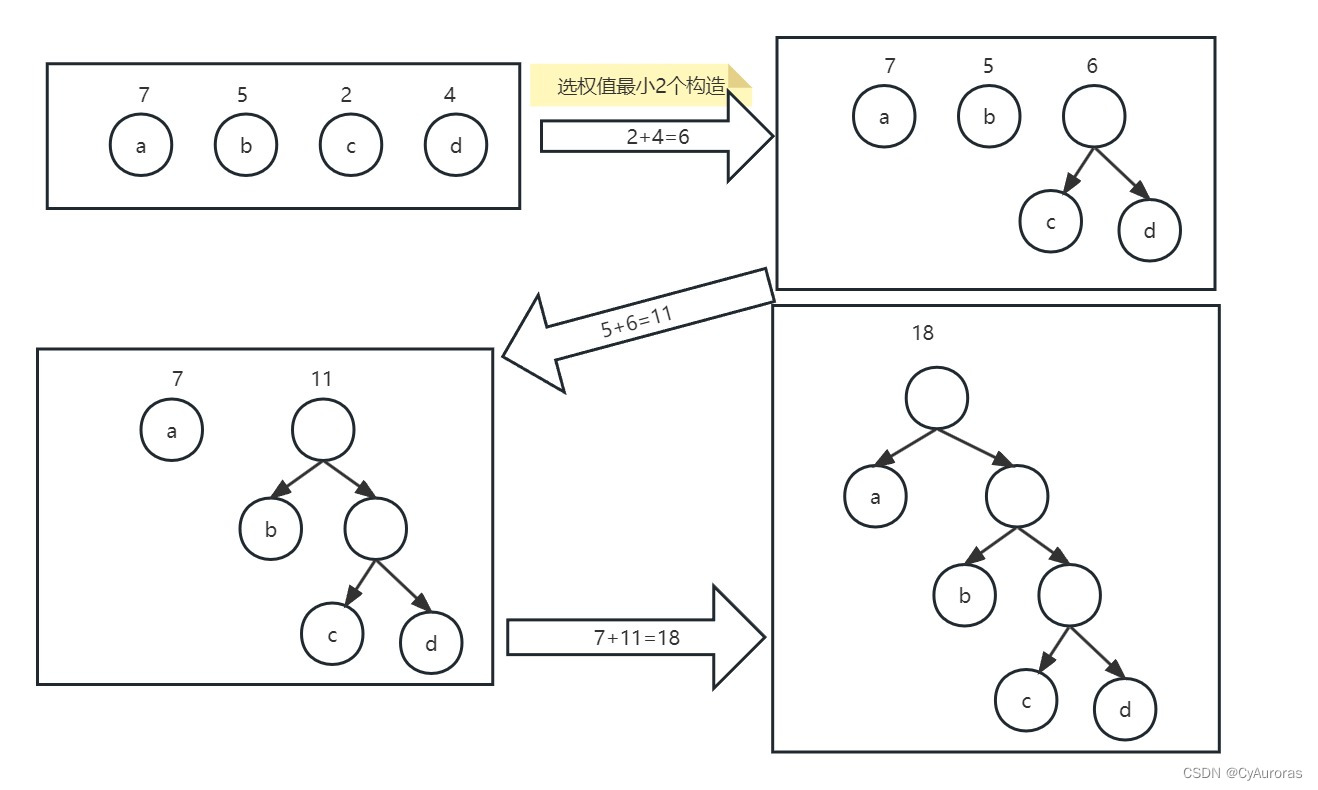
*4.2哈夫曼树构造

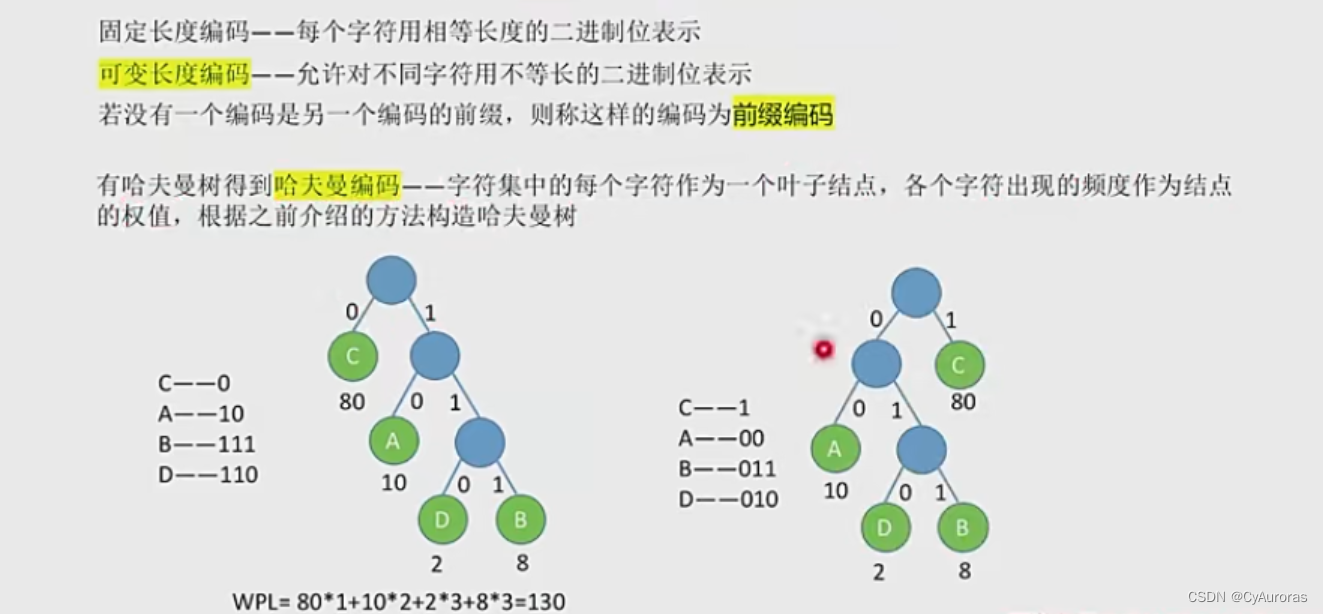
*4.3哈夫曼编码

 五、并查集

*5.1 并查集里题