大家好,我是微学AI,今天给大家介绍一下人工智能基础部分14-蒙特卡洛方法在人工智能中的应用及其Python实现,在人工智能领域,蒙特卡洛方法(Monte Carlo Method, MCM)被广泛应用于各种问题的求解。本文首先将介绍蒙特卡洛方法的基本原理和特点,然后通过一个实际问题来演示如何在 Python 中实现该方法,最后给出完整的项目目录结构和具体实现代码,帮助读者更好地理解和掌握这一方法。
一、蒙特卡洛方法简介
蒙特卡洛方法是通过随机数进行数据模拟和数值计算的一种方法。它的基本思想是通过随机抽样进行计算或模拟,然后对估计结果进行统计分析。蒙特卡洛方法最初是用于求解概率问题,例如对于一个掷骰子的游戏,要求掷出6的概率,可以通过大量的模拟实验来估计这个概率。
蒙特卡洛方法在计算机科学、物理学、金融学、生物学等领域都有广泛的应用。在物理学中,蒙特卡洛方法可以用来模拟分子的运动和相互作用,以及求解复杂的高能物理问题。在金融学中,蒙特卡洛方法可以用来估计期权的价格和风险,以及进行投资组合优化。
蒙特卡洛方法,又称统计模拟方法,是一种通过随机抽样的方式求解各种问题的数值计算方法。在 AI 领域,它被广泛应用于搜索策略、强化学习、博弈论等多个方面。
蒙特卡洛方法的主要特点有:
1. 基于随机采样:通过反复随机抽样实现对问题的求解,从而避免了穷举和解析方法所面临的计算复杂度问题。
2. 简单易行:算法实现相对简单,通常需要编写较少的代码,并且容易调试。
3. 并行性强:方法本身没有严格的先后顺序,适合于并行计算和分布式计算。
4. 收敛性:随着采样数据的逐渐增多,计算结果将逐步接近于真实值,具有较好的收敛性。
二、蒙特卡洛方法原理
蒙特卡洛方法的基本思想是将问题转化为一个随机实验。通过构造适当的随机变量来模拟该实验,并通过对随机变量的反复抽样来求出问题的近似解。
蒙特卡洛方法的关键步骤:
1. 确定问题的随机模型和随机变量;
2. 进行随机抽样模拟;
3. 根据模拟结果求取问题的解。
三、示例:计算圆周率
计算圆周率是一个经典的蒙特卡洛方法的应用。假设我们已知一个单位正方形内部包含一个半径为 1 的圆,我们可以通过随机采样的方法计算该正方形内部的点落在圆内的概率,从而估计圆周率。我们使用 random.uniform() 函数来生成随机数,计算随机点 (x, y) 落在圆内的概率。然后根据比例计算圆周率。
import random
def monte_carlo_pi(num_samples):
num_points_in_circle = 0
for _ in range(num_samples):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
distance = x*x + y*y
if distance <= 1:
num_points_in_circle += 1
return 4 * num_points_in_circle / num_samples
def test_monte_carlo_pi():
pi_estimate = monte_carlo_pi(100000)
print(f"评估 圆周率约为: {pi_estimate}")
if __name__ == "__main__":
test_monte_carlo_pi()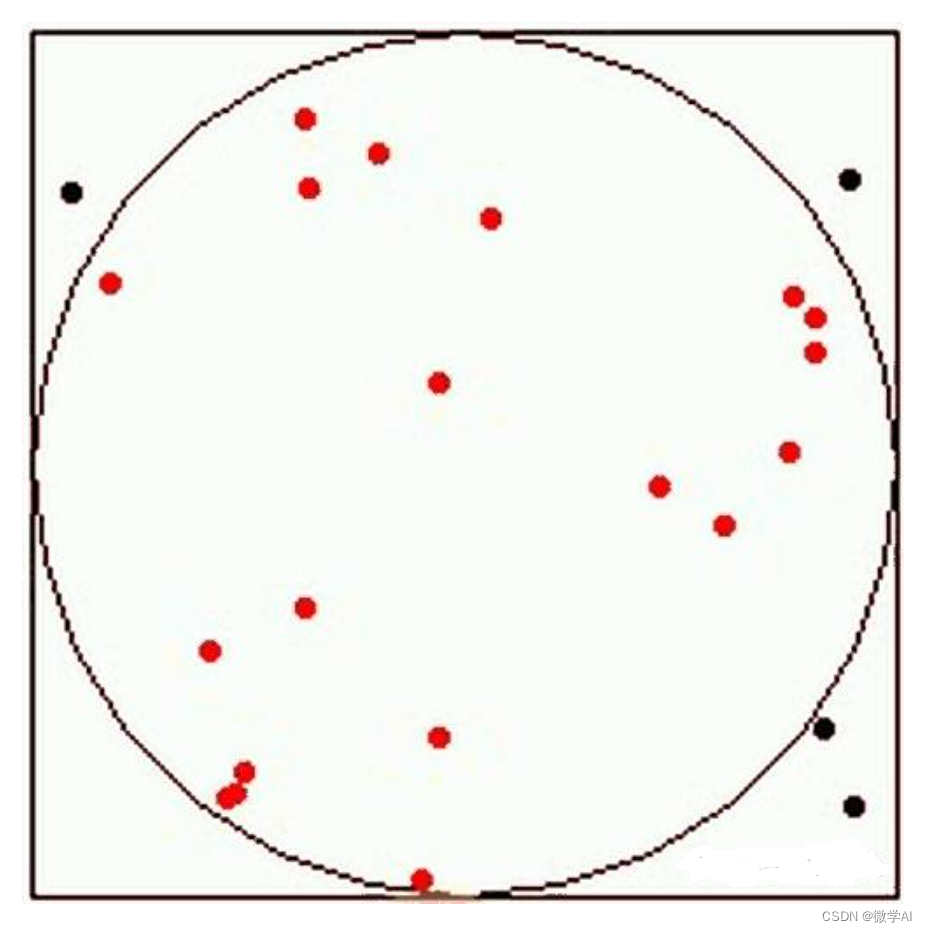
运行结果:
评估 圆周率约为: 3.14036我们得到圆周率的近似解 3.14036,随着num_samples的增大,圆周率的近似解会更加接近真实值。
本文通过详细介绍了蒙特卡洛方法在 AI 领域的应用及其 Python 实现,希望能帮助读者更好地掌握这一方法,并在实际问题中灵活运用。