【力扣周赛】第344场周赛

news2024/11/24 6:56:59

【力扣周赛】第344场周赛

    • 6416：找出不同元素数目差数组
      • 题目描述
      • 解题思路
    • 6417：频率跟踪器
      • 题目描述
      • 解题思路
    • 6418：有相同颜色的相邻元素数目
      • 题目描述
      • 解题思路
    • 6419：使二叉树所有路径值相等的最小代价
      • 题目描述
      • 解题思路

6416：找出不同元素数目差数组

题目描述

描述：给你一个下标从 0 开始的数组 nums ，数组长度为 n 。

nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示，其中 diff[i] 等于前缀 nums[0, …, i] 中不同元素的数目 减去 后缀 nums[i + 1, …, n - 1] 中不同元素的数目。

返回 nums 的 不同元素数目差 数组。

注意 nums[i, …, j] 表示 nums 的一个从下标 i 开始到下标 j 结束的子数组（包含下标 i 和 j 对应元素）。特别需要说明的是，如果 i > j ，则 nums[i, …, j] 表示一个空子数组。

输入：nums = [1,2,3,4,5]
输出：[-3,-1,1,3,5]
解释：
对于 i = 0，前缀中有 1 个不同的元素，而在后缀中有 4 个不同的元素。因此，diff[0] = 1 - 4 = -3 。
对于 i = 1，前缀中有 2 个不同的元素，而在后缀中有 3 个不同的元素。因此，diff[1] = 2 - 3 = -1 。
对于 i = 2，前缀中有 3 个不同的元素，而在后缀中有 2 个不同的元素。因此，diff[2] = 3 - 2 = 1 。
对于 i = 3，前缀中有 4 个不同的元素，而在后缀中有 1 个不同的元素。因此，diff[3] = 4 - 1 = 3 。
对于 i = 4，前缀中有 5 个不同的元素，而在后缀中有 0 个不同的元素。因此，diff[4] = 5 - 0 = 5 。

输入：nums = [3,2,3,4,2]
输出：[-2,-1,0,2,3]
解释：
对于 i = 0，前缀中有 1 个不同的元素，而在后缀中有 3 个不同的元素。因此，diff[0] = 1 - 3 = -2 。
对于 i = 1，前缀中有 2 个不同的元素，而在后缀中有 3 个不同的元素。因此，diff[1] = 2 - 3 = -1 。
对于 i = 2，前缀中有 2 个不同的元素，而在后缀中有 2 个不同的元素。因此，diff[2] = 2 - 2 = 0 。
对于 i = 3，前缀中有 3 个不同的元素，而在后缀中有 1 个不同的元素。因此，diff[3] = 3 - 1 = 2 。
对于 i = 4，前缀中有 3 个不同的元素，而在后缀中有 0 个不同的元素。因此，diff[4] = 3 - 0 = 3 。

解题思路

难度：简单。

思路：最直观的想法是，使用一个数组prefix[i]表示前缀nums[0…i]中不同元素的数目，使用一个数组postfix[i]表示后缀nums[i+1…n-1]中不同元素的数目，使用一个数组res[i]表示前缀数目减去后缀数目，使用一个uset1存储从前向后遍历的不重复的元素，使用一个uset2存储从后向前遍历的不重复的元素。首先从前向后遍历填充prefix，若当前元素在uset1中找不到则prefix[i]=prefix[i-1]+1并将其插入uset1，反之则prefix[i]=prefix[i-1]；接着从后向前遍历填充postfix，若当前元素在uset2中找不到则prefix[i]=prefix[i+1]+1并将其插入uset2，反之则postfix[i]=postfix[i+1]；最后从前向后遍历填充res，其为res[i]=prefix[i]-postfix[i]。注意边界条件的处理喔！

class Solution {
public:
    vector<int> distinctDifferenceArray(vector<int>& nums) {
        int n=nums.size();
        vector<int> prefix(n,0);
        prefix[0]=1;
        vector<int> postfix(n,0);
        postfix[n-1]=1;
        vector<int> res(n,0);
        if(n==1)
        {
            res[0]=prefix[0]-0;
            return res;
        }
        unordered_set<int> uset1;
        uset1.emplace(nums[0]);
        unordered_set<int> uset2;
        uset2.emplace(nums[n-1]);
        //填充前缀数组
        cout<<"prefix:";
        for(int i=1;i<n;i++)
        {
            //出现重复
            if(uset1.find(nums[i])!=uset1.end())
                prefix[i]=prefix[i-1];
            //第一次出现
            else
            {
                prefix[i]=prefix[i-1]+1;
                uset1.emplace(nums[i]);
            }
            cout<<prefix[i]<<" ";
        }
        cout<<endl;
        //填充后缀数组
        cout<<"postfix:";
        for(int i=n-2;i>=0;i--)
        {
            //出现重复
            if(uset2.find(nums[i])!=uset2.end())
                postfix[i]=postfix[i+1];
            //第一次出现
            else
            {
                postfix[i]=postfix[i+1]+1;
                uset2.emplace(nums[i]);
            }
            cout<<postfix[i]<<" ";
        }
        cout<<endl;
        for(int i=0;i<n-1;i++)
            res[i]=prefix[i]-postfix[i+1];
        res[n-1]=prefix[n-1]-0;
        return res;
    }
};

优化：其实可以使用prefix.size()表示前缀数目，使用postfix.size()表示后缀数目。既然prefix和res均是从前向后遍历，则可以将其合并处理，即先后向遍历推出postfix，然后前向遍历推出prefix和res。

vector<int> distinctDifferenceArray(vector<int>& nums) 
{
   int n=nums.size();
   vector<int> prefix(n,0);    //前缀数目
   vector<int> postfix(n,0);   //后缀数目
   vector<int> res(n,0);       //结果数组
   unordered_set<int> uset1;   //前向遍历不重复元素
   unordered_set<int> uset2;   //后向遍历不重复元素
   //后向遍历填充后缀数组
   for(int i=n-1;i>=0;i--)
   {
       postfix[i]=uset2.size();
       uset2.emplace(nums[i]);  //存在则插入 不存在则啥也不做
   }
   //前向遍历填充前缀数组和结果数组
   for(int i=0;i<n;i++)
   {
       uset1.emplace(nums[i]);
       prefix[i]=uset1.size();
       res[i]=prefix[i]-postfix[i];
   }
   return res;
}

6417：频率跟踪器

题目描述

描述：请你设计并实现一个能够对其中的值进行跟踪的数据结构，并支持对频率相关查询进行应答。

实现 FrequencyTracker 类：

FrequencyTracker()：使用一个空数组初始化 FrequencyTracker 对象。
void add(int number)：添加一个 number 到数据结构中。
void deleteOne(int number)：从数据结构中删除一个 number 。数据结构 可能不包含 number ，在这种情况下不删除任何内容。
bool hasFrequency(int frequency): 如果数据结构中存在出现 frequency 次的数字，则返回 true，否则返回 false。

输入
["FrequencyTracker", "add", "add", "hasFrequency"]
[[], [3], [3], [2]]
输出
[null, null, null, true]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.add(3); // 数据结构现在包含 [3, 3]
frequencyTracker.hasFrequency(2); // 返回 true ，因为 3 出现 2 次

输入
["FrequencyTracker", "add", "deleteOne", "hasFrequency"]
[[], [1], [1], [1]]
输出
[null, null, null, false]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(1); // 数据结构现在包含 [1]
frequencyTracker.deleteOne(1); // 数据结构现在为空 []
frequencyTracker.hasFrequency(1); // 返回 false ，因为数据结构为空

输入
["FrequencyTracker", "hasFrequency", "add", "hasFrequency"]
[[], [2], [3], [1]]
输出
[null, false, null, true]

解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.hasFrequency(2); // 返回 false ，因为数据结构为空
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.hasFrequency(1); // 返回 true ，因为 3 出现 1 次

解题思路

难度：中等。

思路：最直观的想法是，使用一个umap存储元素以及其对应的次数。add则直接将number对应次数加一；deleteOne则先判断umap中是否存在该元素，如果存在，如果该元素出现的次数大于等于1则将其对应次数减一，如果该元素出现的次数等于0则将其从umap中删除；hasFrequency则遍历umap，如果其对应的次数等于frequency，则直接返回true，反之如果遍历完umap还未找到则返回false。（超出时间限制：有两个测试案例无法通过）

unordered_map<int,int> umap;
FrequencyTracker()
{
}
void add(int number) 
{
   umap[number]++;
}
void deleteOne(int number) 
{
   if(umap.find(number)!=umap.end())
   {
       if(umap[number]>=1)
          umap[number]--;
       if(umap[number]==0) //减完后剩余0
          umap.erase(number);
   }
}
bool hasFrequency(int frequency) 
{
    for(auto it:umap)
    {
       if(it.second==frequency)
         return true;
    }
    return false;
}

优化：既然上述超时，那么推测可能是因为hasFrequency函数的一层循环，那么是否可以不用循环也能判断呢？第一想法是使用空间换时间！用两个哈希！一开始想的是存储次数和对应的元素，但是写着写着发现太复杂了，后来一想根本不需要关心对应的元素有哪些，只需要关心次数出现的个数啦，于是第二个哈希就是次数以及对应的个数。注意，使用两个哈希在删除时需要额外小心！只有大于等于1才减去，且减完后等于0则要删除。

unordered_map<int,int> umap;  //<数值，次数>
unordered_map<int,int> nmap;  //<次数，个数>
FrequencyTracker() 
{
}  
void add(int number) 
{
   if(umap[number]>=1)  //以前出现过则将以前出现过的次数的个数减一
   {
        nmap[umap[number]]--;
        if(nmap[umap[number]]==0)
          nmap.erase(umap[number]);
   }
   umap[number]++;  //更改出现过的次数
   nmap[umap[number]]++;  //将当前出现过的次数的个数加一
}
void deleteOne(int number) 
{
   if(umap.find(number)!=umap.end())
   {
      if(umap[number]>=1)  //出现次数大于等于1
      {
          nmap[umap[number]]--; //将出现过的次数的个数减一
          if(nmap[umap[number]]==0)
             nmap.erase(umap[number]);
          umap[number]--; //更改出现过的次数
          if(umap[number]==0) //减完后剩余0
              umap.erase(number);
          else if(umap[number]>0)  //如果减完后还有次数
              nmap[umap[number]]++;  //将当前出现过的次数的个数加一
      }
    }
} 
bool hasFrequency(int frequency) 
{
    if(nmap.find(frequency)!=nmap.end())
        return true;
    return false;
}

优化：其实该题可以直接使用双map，但是不需要上述这么复杂，直接对出现的次数的个数进行加减处理即可，同时在删除时对元素出现的次数进行特殊判断，即小于等于0则返回。

unordered_map<int,int> umap;
unordered_map<int,int> nmap;
FrequencyTracker() 
{
}
void add(int number) 
{
    nmap[umap[number]]--;
    nmap[++umap[number]]++;
}
void deleteOne(int number) 
{
    if(umap[number]<=0) return; //为0不做任何处理
    nmap[umap[number]]--;
    nmap[--umap[number]]++;
}
bool hasFrequency(int frequency) 
{
    return nmap[frequency]>=1?true:false;
}

6418：有相同颜色的相邻元素数目

题目描述

描述：给你一个下标从 0 开始、长度为 n 的数组 nums 。一开始，所有元素都是 未染色 （值为 0 ）的。

给你一个二维整数数组 queries ，其中 queries[i] = [indexi, colori] 。

对于每个操作，你需要将数组 nums 中下标为 indexi 的格子染色为 colori 。

请你返回一个长度与 queries 相等的数组 answer ，其中 answer[i]是前 i 个操作 之后 ，相邻元素颜色相同的数目。

更正式的，answer[i] 是执行完前 i 个操作后，0 <= j < n - 1 的下标 j 中，满足 nums[j] == nums[j + 1] 且 nums[j] != 0 的数目。

输入：n = 4, queries = [[0,2],[1,2],[3,1],[1,1],[2,1]]
输出：[0,1,1,0,2]
解释：一开始数组 nums = [0,0,0,0] ，0 表示数组中还没染色的元素。
- 第 1 个操作后，nums = [2,0,0,0] 。相邻元素颜色相同的数目为 0 。
- 第 2 个操作后，nums = [2,2,0,0] 。相邻元素颜色相同的数目为 1 。
- 第 3 个操作后，nums = [2,2,0,1] 。相邻元素颜色相同的数目为 1 。
- 第 4 个操作后，nums = [2,1,0,1] 。相邻元素颜色相同的数目为 0 。
- 第 5 个操作后，nums = [2,1,1,1] 。相邻元素颜色相同的数目为 2 。

输入：n = 1, queries = [[0,100000]]
输出：[0]
解释：一开始数组 nums = [0] ，0 表示数组中还没染色的元素。
- 第 1 个操作后，nums = [100000] 。相邻元素颜色相同的数目为 0 。

解题思路

有相同颜色的相邻元素数目：最直观的想法是，使用nums数组表示染色数组，初始化为0表示未染色，使用res表示结果数组，使用ans表示结果项，其表示相邻元素颜色相同的数目，初始化为0。遍历queries数组，使用index接收下标，使用color接收染色值。首先把原来的颜色去掉，即如果原本已经染色并且其与相邻元素相等，则将ans减一；然后修改颜色；最后加上修改后的颜色，即如果修改后已经染色并且其与相邻元素相等，则将ans加一。

vector<int> colorTheArray(int n, vector<vector<int>>& queries) 
{
   // 长度为n的nums初始元素均为0
   vector<int> nums(n,0); //染色数组 初始为0表示未染色
   vector<int> res;  //结果数组
   int ans = 0;   //结果项 表示相邻元素颜色相同的数目
   for(auto query:queries) //遍历数组  修改颜色只会影响相邻元素
   {
      //query=[index,color] //下标 染色值
      int index = query[0];
      int color = query[1];
      //把原来的颜色去掉 未染色才能比较是否相等
      if(nums[index]!=0&&index-1>=0&&nums[index]==nums[index-1]) ans--;
      if(nums[index]!=0&&index+1<n&&nums[index]==nums[index+1]) ans--;
      //修改颜色
      nums[index]=color;
      //加上修改后的颜色
      if(nums[index]!=0&&index-1>=0&&nums[index]==nums[index-1]) ans++;
      if(nums[index]!=0&&index+1<n&&nums[index]==nums[index+1]) ans++;
      res.push_back(ans);
    }
    return res;
}

6419：使二叉树所有路径值相等的最小代价

题目描述

描述：给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
路径值 指的是路径上所有节点的值之和。

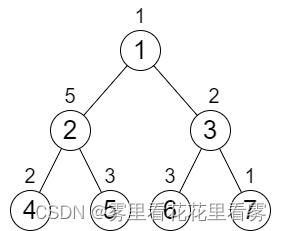
在这里插入图片描述

输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

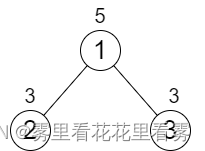
在这里插入图片描述

输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

解题思路

使二叉树所有路径值相等的最小代价：最直观的想法是，使用ans表示最少操作次数。首先从满二叉树的最后一个非叶子节点开始遍历，取其两个子结点的差值绝对值加入ans中，即表明操作使得其子结点均为两者中的最大值，接着将两者中的最大值加入到其父节点的代价cost中，继续向上传递，直到传到根节点为止。

int minIncrements(int n, vector<int>& cost) 
{
    // 满二叉树 可以使用数组表示
    int ans=0; //表示最少操作次数
    for(int i=n/2;i>0;i--) //i表示节点编号 如果对应数组的话要减一
    {
        ans+=abs(cost[2*i-1]-cost[2*i]);  //取兄弟节点的差值绝对值
        cost[i-1]+=max(cost[2*i-1],cost[2*i]); //将子节点代价加上
    }
    return ans;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/499861.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++ ---- 类和对象（上）

C++ ---- 类和对象（上）

目录 本节目标 常见问题 面向过程和面向对象的理解 什么是类如何定义类 类的引入 类的定义 类的两种定义习惯 类的作用域 类的访问限定符 访问限定符介绍 封装 封装的意义 类的实例化 类对象模型 类对象的存储方式 结构体对齐 计算类对象的大小 this指针 问题…
阅读更多...
数青蛙​、[USACO10FEB]Chocolate Giving S

数青蛙​、[USACO10FEB]Chocolate Giving S

一、1419. 数青蛙 思路 这道题有俩种解法&#xff0c;一是记数&#xff0c;二是贪心 记数&#xff1a; 这是官方的题解 我们用frog_ num来表示现在正在发出蛙鸣声的青蛙数目&#xff0c;用cnt[c] 示已经发出-次有效蛙鸣中的字符c的青蛙个数,比如当cnt[c] 2时表示当前有2只…
阅读更多...
[mini LCTF 2023] 西电的部分

[mini LCTF 2023] 西电的部分

感觉比赛还是很不错&#xff0c;就是有点难了&#xff0c;不过都是简单题重复更没意思。作出一道来就有一点收获。 misc1 签到题也不简单&#xff0c;已经很久不作misc了&#xff0c;感觉这东西需要安的东西太多&#xff0c;怕机子累坏了。 一个复合的wav声音文件&#xff0…
阅读更多...
【Android入门到项目实战-- 8.5】—— 使用HTTP协议访问网络的实践用法

【Android入门到项目实战-- 8.5】—— 使用HTTP协议访问网络的实践用法

目录 准备工作 一、创建HttpUtil类 二、调用使用 一个应用程序可能多次使用到网络功能&#xff0c;这样就会大量代码重复&#xff0c;通常情况下我们应该将这些通用的网络操作封装到一个类里&#xff0c;并提供一个静态方法&#xff0c;想要发送网络请求的时候&#xff0c;只…
阅读更多...
【c语言】字符串匹配(搜索) | API仿真

【c语言】字符串匹配(搜索) | API仿真

c语言系列专栏&#xff1a;c语言之路重点知识整合 字符串知识点&#xff1a;字符串基本概念、存储原理 字符串匹配 目录 一、字符串匹配二、strstr仿真声明&#xff1a;指针方式定义&#xff1a;调用测试&#xff1a;运行结果&#xff1a; 一、字符串匹配 字符串匹配是对一个…
阅读更多...
HttpClient连接池使用不当问题分析解决

HttpClient连接池使用不当问题分析解决

目录 背景代码实现工具类功能实现模拟使用 问题分析与定位解决方案总结 背景 最近遇到一个HttpClient问题&#xff0c;某个接口一直报404错误。该接口使用HttpClient调用其他服务获取数据&#xff0c;为了提高接口调用性能&#xff0c;利用httpclient池化技术来保证请求的数量…
阅读更多...
嵌入式中利用软件实现定时器的两种方法分析

嵌入式中利用软件实现定时器的两种方法分析

目录 第一&#xff1a;简介 第二&#xff1a;链表实现方式 第三&#xff1a;结构体实现方式 第一&#xff1a;简介 在一般的嵌入式产品设计中&#xff0c;介于成本、功耗等&#xff0c;所选型的MCU基本都是资源受限的&#xff0c;而里面的定时器的数量更是有限。在我们软件…
阅读更多...
Origin如何绘制基础图形？

Origin如何绘制基础图形？

文章目录 0.引言1.绘图操作2.图形设置3.图形标注 0.引言 因科研等多场景需要绘制专业的图表&#xff0c;笔者对Origin进行了学习&#xff0c;本文通过《Origin 2022科学绘图与数据》及其配套素材结合网上相关资料进行学习笔记总结&#xff0c;本文对绘制基础图形进行阐述。 1.…
阅读更多...
2023.5.7 第五十二次周报

2023.5.7 第五十二次周报

目录 前言 文献阅读&#xff1a;基于BO-EMD-LSTM模型预测教室长期二氧化碳浓度 背景 思路 BO-EMD-LSTM 混合模型 EMD 算法 与其他模型的比较 结论 论文代码 总结 前言 This week, I studied an article that uses LSTM to predict gas concentration.This study wa…
阅读更多...
Springboot +Flowable，按角色分配任务

Springboot +Flowable，按角色分配任务

一.简介 在为 UserTask 设置处理人的时候&#xff0c;除了设置单个的处理人&#xff0c;也可以设置 Group&#xff08;分组&#xff09;&#xff0c;就是某一个用户组内的所有用户都可以处理该 Task。 二.绘制流程图 首先我们还是使用之前旧的流程图&#xff0c;流程图截图如…
阅读更多...
从0学Spring Boot框架（Spring Boot配置文件与Spring Boot日志文件）

从0学Spring Boot框架（Spring Boot配置文件与Spring Boot日志文件）

文章目录 1. 什么是Spring Boot&#xff1f;2. 如何创建Spring Boot项目&#xff1f;3. 验证Spring Boot项目的创建3.1 补充添加依赖3.2 代码示例 4. Spring Boot配置文件4.1 配置文件的作用4.2 配置文件的格式4.2.1 properties的语法4.2.2 yml的语法4.2.3 properties与yml的对…
阅读更多...
想把PDF转成Word？这三个免费在线工具不容错过！

想把PDF转成Word？这三个免费在线工具不容错过！

在日常工作和学习中&#xff0c;我们经常会遇到需要将PDF文件转为Word文档的情况。本文将介绍三种不同的PDF转Word的方法。 首先是推荐的PDF转Word网站&#xff1a;记灵在线工具&#xff08;http://remeins.com)。 这是一个功能非常强大的PDF在线处理网站&#xff0c;可以完全…
阅读更多...
CNI_02_Flannel 跨主机通信Overlay Network三种实现

CNI_02_Flannel 跨主机通信Overlay Network三种实现

文章目录 一、前言二、跨主机网络三、UDP模式四、VXLAN模式4.1 VXLAN完全在内核态中构建Overlay Netwok覆盖网络4.2 VXLAN模式整个流程步骤1&#xff1a;网络请求从容器到宿主机步骤2&#xff1a;根据目的容器IP在Node1宿主机上找到正确的route路由步骤3&#xff1a;构建内部数…
阅读更多...
深度学习实战项目(一)-基于cnn和opencv的车牌号识别

深度学习实战项目(一)-基于cnn和opencv的车牌号识别

深度学习实战项目(一)-基于cnn和opencv的车牌号识别 网上大部分是关于tensorflow&#xff0c;使用pytorch的比较少&#xff0c;本文也在之前大佬写的代码的基础上&#xff0c;进行了数据集的完善&#xff0c;和代码的优化&#xff0c;效果可比之前好一点。 数据集 数据集来自…
阅读更多...
AutoCV：Python基础总结

AutoCV：Python基础总结

目录 Python基础总结前言Python基础课程总结第一课&#xff1a;开发环境和基本数据类型第二课&#xff1a;控制流程和函数第三课&#xff1a;闭包和根号2的求解第四课&#xff1a;类和三大神器第五课&#xff1a;文件IO和pickle、json第六课&#xff1a;作用域、模块和包、Data…
阅读更多...
IDM下载器|Windows系统经典下载工具idm6.41|IDM如何在线视频下载工具 |下载视频教程

IDM下载器|Windows系统经典下载工具idm6.41|IDM如何在线视频下载工具 |下载视频教程

IDM全称Internet Download Manager,是一种将下载速度提高最多5倍的专业下载工具,支持大部分文件格式下载和基本所有的下载链接,无视网址本身下载限速,直接达到电脑该有的网速。 下载更快更可靠 下载INTERNET DOWNLOAD MANAGER(IDM下载器)开始您的极速下载旅程&#xff0c;永远…
阅读更多...
鲲志说 我的创作纪念日(2023-05-07)

鲲志说 我的创作纪念日(2023-05-07)

目录 前言有时候缘分就是这么巧&#xff01;努力终会有所获日常规划成就憧憬 前言 今天是个特殊的日子&#xff0c;是我成为创作者的第2048天。但不仅仅是因此今天才特殊&#xff0c;更重要的是因为你&#xff0c;今天才特殊&#xff0c;值得纪念。不管前路如何&#xff0c;积…
阅读更多...
微信小程序开发19__第三方UI组件Vant Weapp的应用

微信小程序开发19__第三方UI组件Vant Weapp的应用

为了提高小程序的开发效率&#xff0c; 可以考虑使用第三方 UI 组件来实现界面的视觉统一。 本文以有赞第三方 UI 组件库 Vant Weapp 为例&#xff0c;介绍如何使用自定义组件 实现一个小程序。 Vant Weapp 是一款轻量、 可靠的小程序UI组件库&#xff0c; 与有赞移动端组…
阅读更多...
数字图像处理-绪论

数字图像处理-绪论

数字图像处理-绪论 文章目录 前言一、闲谈二、什么是数字图像处理&#xff1f;2.1. 什么是数字图像&#xff1f;2.1.1. 可见光图像2.1.2. 不可见光图像 2.2. 什么是数字图像处理&#xff1f; 三、数字图像处理的前世今生3.1. 数字图像处理的前世3.2. 数字图像处理的今生 四、数…
阅读更多...
计网笔记 01 概述 计算机网络体系结构、参考模型

计网笔记 01 概述 计算机网络体系结构、参考模型

文章目录 前言1、计网概述1.1 概念、组成、功能、分类1.1.1 概念1.1.2 计网组成1.1.2 计网分类 1.2 标准化工作及相关组织1.2.1 标准的分类 1.3 性能指标★★★1.3.1 速率相关性能指标1.3.2 时延相关指标 2、体系结构&参考模型★★★★★&#xff08;对应王道视频7-10p 相当…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023