[LeetCode复盘] LCCUP'23春季赛组队赛 20230507
- 一、本周周赛总结
- 1. 符文储备
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 2. 城墙防线
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 3. 提取咒文
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 4. 生物进化录
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 5. 与非的谜题
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- 个人稳定爆零,全靠队友带飞。
- T1 DP。
- T2 二分答案。
- T3 n次多源最短路。
- T4 树上贪心。
- T5 位运算。
- T6 连楼教主都没ac。
1. 符文储备
1. 符文储备
1. 题目描述
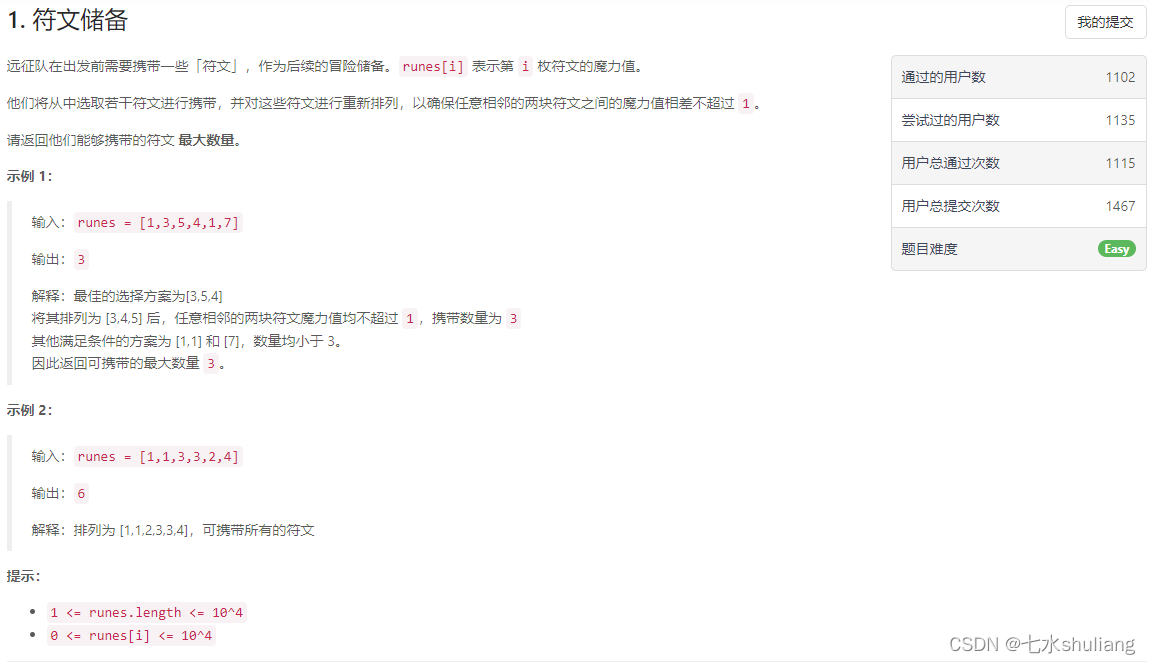
2. 思路分析
- 由于顺序不重要,因此可以让临近的差值变小的方案是排序。
- 那么就是最长子段。
3. 代码实现
class Solution:
def runeReserve(self, runes: List[int]) -> int:
runes.sort()
n = len(runes)
f = [1]*n
for i in range(1,n):
if runes[i]-runes[i-1]<=1:
f[i] += f[i-1]
return max(f)
2. 城墙防线
2. 城墙防线
1. 题目描述

2. 思路分析
二分答案。
- 显然,若x不行,则x+1更不行;x可以,x-1更可以。满足单调性。
- 由于两边是无限的,因此只判断中间的n-2个位置即可。
- 让城墙先优先往左膨胀,剩下的部分向右膨胀。
- 记录每个城墙膨胀完右侧的位置,下一个城墙就可以向左尽量延伸。
3. 代码实现
class Solution:
def rampartDefensiveLine(self, a: List[List[int]]) -> int:
n = len(a)
def ok(x):
p = a[0][1] # 前一个城墙右端扩展到哪
for i in range(1,n-1):
l,r = a[i]
if l - p>=x:
p = r
else:
p = r + x - l + p
if p > a[i+1][0]:
return True
return False
return bisect_left(range(10**9),True,key=ok)-1
3. 提取咒文
3. 提取咒文
1. 题目描述
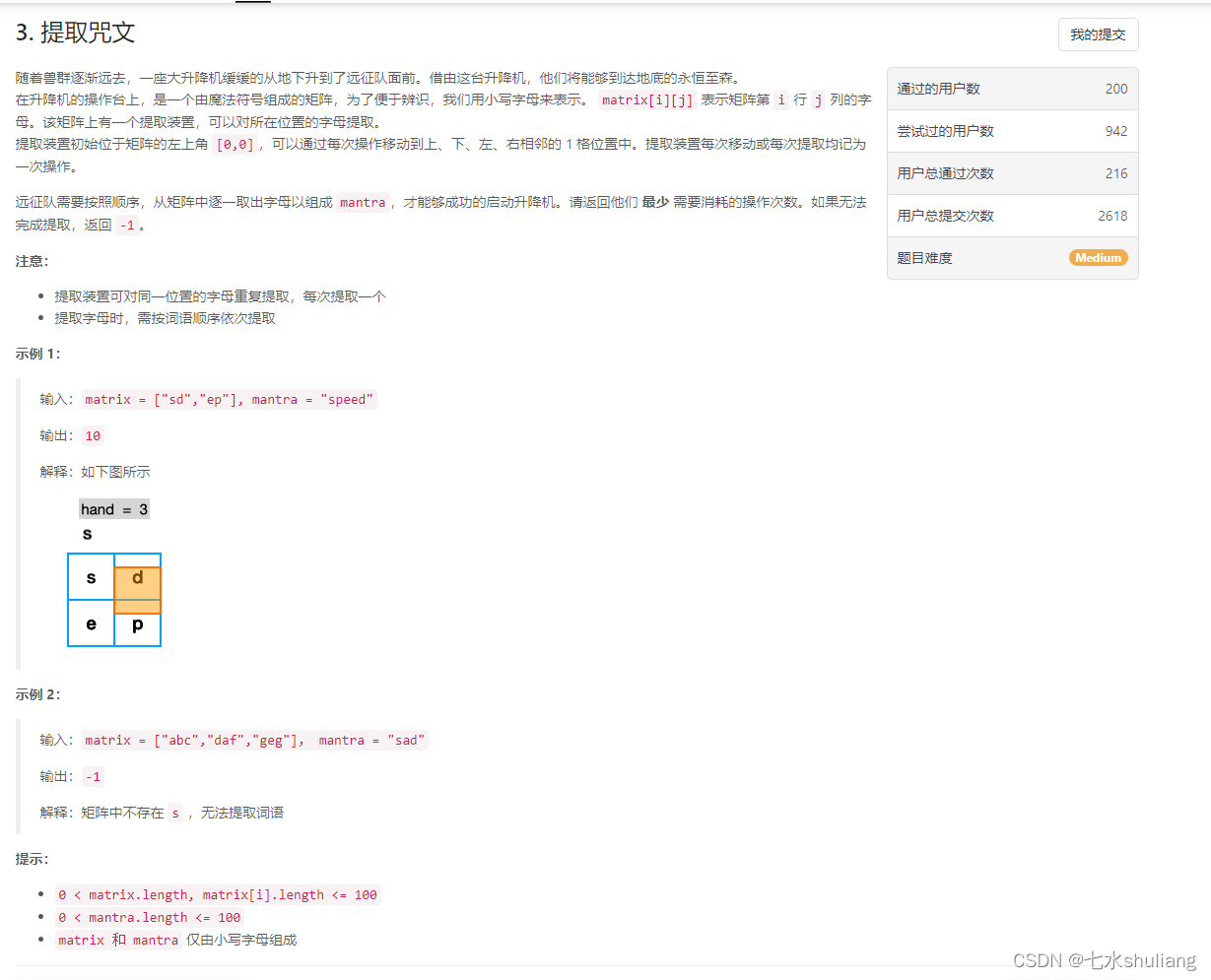
2. 思路分析
上来就做t3卡了一个小时,真的难受。
- 对于每个字符,都跑一遍多源最短路,看看从上一个字符来的花费。
- 然后用dist建立新的q,去跑下一个字符。
- 注意用dir4个方向去跑,这样转移就是4,复杂度控制在lennmlgnm。
3. 代码实现
class Solution:
def extractMantra(self, g: List[str], s: str) -> int:
m,n = len(g),len(g[0])
p = set()
for row in g:
p|=set(row)
if any(c not in p for c in s):
return -1
idx = defaultdict(list)
for i,row in enumerate(g):
for j,c in enumerate(row):
idx[c].append((i,j))
q = [(0,0,0)]
for c in s:
dist = [[inf]*n for _ in range(m)]
for d,x,y in q:
dist[x][y] = d
while q:
d,x,y = heappop(q)
if d > dist[x][y]:continue
for a,b in (x+1,y),(x-1,y),(x,y+1),(x,y-1):
if 0<=a<m and 0<=b<n:
p = d+1
if p<dist[a][b]:
dist[a][b] = p
heappush(q,(p,a,b))
q = []
for i,j in idx[c]:
q.append((dist[i][j]+1,i,j))
q.sort()
return min(dist[x][y]+1 for x,y in idx[s[-1]])
4. 生物进化录
4. 生物进化录
1. 题目描述

2. 思路分析
- 令dfs(u)为计算u这颗子树结束后返回u的最短路径。
- 那么对于所有子树,优先要把字典序小的排到前边。但这个顺序应该判断两个字符串加起来后比较。具体看代码。
- 最后把后缀的1去除即可。
3. 代码实现
class Solution:
def evolutionaryRecord(self, parents: List[int]) -> str:
n = len(parents)
g = [[] for _ in range(n)]
z = -1
for i,f in enumerate(parents):
if f == -1:
z = i
else:
g[f].append(i)
def cmp(a,b):
s1 = a+ b
s2 = b+a
return -1 if s1<s2 else 1
def dfs(u):
x = []
for v in g[u]:
a = dfs(v)
x.append('0'+a+'1')
if not x:
return ''
x.sort(key=cmp_to_key(cmp))
return ''.join(x) # 返回根,不返回
b = dfs(z)
return b.rstrip('1')
5. 与非的谜题
5. 与非的谜题
1. 题目描述
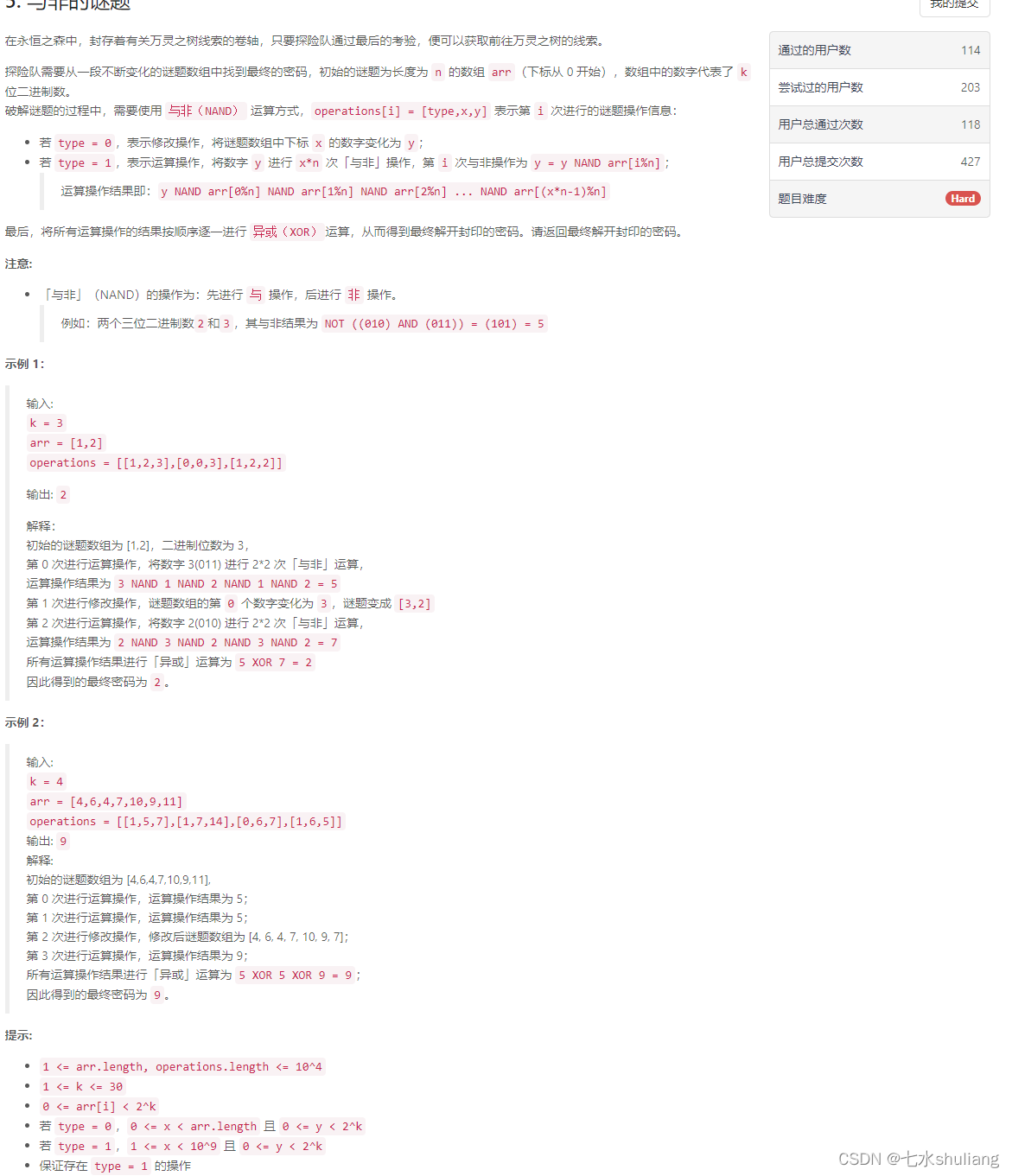
2. 思路分析
- 先观察与非操作,总结一下:
- 0 NAND 0 = 1
- 0 NAND 1 = 1
- 1 NAND 0 = 1
- 1 NAND 1 = 0
- 我们发现但凡操作里有0则结果是0。
- 若操作里是1,则把另个数翻转。
- 考虑若k=1,即arr和y里只有0和1。那么每次type=1的操作,分类讨论:
- 若a[-1]==0,则ans = 1
- 若a[-1]==1,则会在最后一步被翻转;若前边还是1,则还是翻转。
- 那么计算a末尾1的长度p,前边那个0会使ans变成1,后边p个1会使1翻转p次,考虑奇偶即可。
- 若a中干脆没有0,则会被翻转p=x*n次,同样考虑p的奇偶性即可;但这时初始不是1,而是y。
- 上边讨论了只有1位的情况,对于k位,分别计算即可。
- 一开始我写了树状数组二分来计算后缀1的长度,复杂度nklgnlgn,TLE。
- 后来换了SortedList过了,用SortedList记录每位里0的位置,n减去最后一个0的位置就是后缀1的长度。
3. 代码实现
from sortedcontainers import SortedList
class Solution:
def getNandResult(self, k: int, arr: List[int], operations: List[List[int]]) -> int:
n = len(arr)
trees = [SortedList() for _ in range(k)]
for i,v in enumerate(arr):
for j in range(k):
if (v>>j)&1==0:
trees[j].add(i)
ans = 0
for t,x,y in operations:
if t == 0:
for j in range(k):
trees[j].discard(x)
if (y>>j)&1==0:
trees[j].add(x)
else:
z = 0
for j in range(k):
tree = trees[j]
if len(tree)==n:
z|= 1<<j
continue
if not tree:
p = x*n
r = (y>>j)&1
if p&1:
r ^= 1
z|= r<<j
else:
r = 1
p = n - tree[-1]-1
if p&1:
r^=1
z |= r<<j
# print(z)
ans ^= z
return ans