力扣关于平衡二叉树的题目还是有一些的，并且都非常经典，推荐大家练习。今天给大家精选了 4 道题，如果你彻底搞明白了这几道题，碰到其他的平衡二叉树的题目应该不至于没有思路。当你领会了我的思路之后， 建议再找几个题目练手，巩固一下学习成果。

110. 平衡二叉树（简单）

最简单的莫过于判断一个树是否为平衡二叉树了，我们来看下。

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7
返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4
返回 false

思路

由于平衡二叉树定义为就是一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

用伪代码描述就是：

if abs(高度(root.left) - 高度(root.right)) <= 1
   and root.left 也是平衡二叉树 
   and root.right 也是平衡二叉树:
   
    print('是平衡二叉树')
    
else:
    print('不是平衡二叉树')

而 root.left 和 root.right 如何判断是否是二叉平衡树就和 root 是一样的了，可以看出这个问题有明显的递归性。

因此我们首先需要知道如何计算一个子树的高度。这个可以通过递归的方式轻松地计算出来。计算子树高度的 Python

代码如下：

def dfs(node):
    if not node: return 0
    
    l = dfs(node.left)
    r = dfs(node.right)
    
    return max(l, r) + 1

代码

代码支持： Python3

Python3 Code:

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def dfs(node):
            if not node: return 0
            l = dfs(node.left)
            r = dfs(node.right)
            return max(l, r)  + 1
            
        if not root: return True
        if abs(dfs(root.left) -  dfs(root.right)) > 1: return False
        return self.isBalanced(root.left) and self.isBalanced(root.right)

复杂度分析

• 时间复杂度：对于 isBalanced 来说，由于每个节点最多被访问一次，这部分的时间复杂度为 $O(N)$，而 dfs 函数 每次被调用的次数不超过 $logN$，因此总的时间复杂度为 $O(NlogN)$，其中 $N$ 为 树的节点总数。
• 空间复杂度：由于使用了递归，这里的空间复杂度的瓶颈在栈空间，因此空间复杂度为 $O(h)$，其中 $h$ 为树的高度。

108. 将有序数组转换为二叉搜索树（简单）

108 和 109 基本是一样的，只不过数据结构不一样，109 变成了链表了而已。由于链表操作比数组需要考虑更多的因素，因此 109 是 中等难度。

题目描述

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

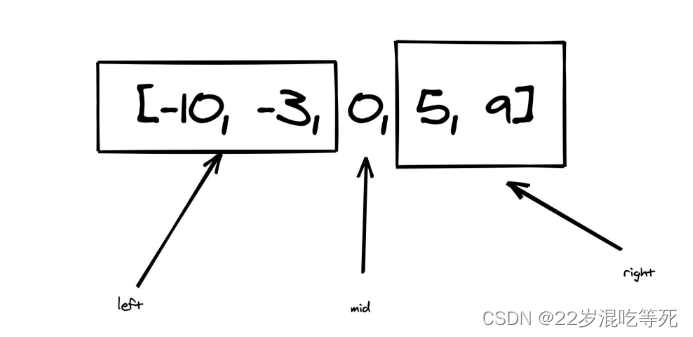
给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

思路

对于这个问题或者 给定一个二叉搜索树，将其改为平衡（后面会讲） 基本思路都是一样的。

题目的要求是将有序数组转化为：

• 高度平衡的二叉树
• 二叉搜索树

由于平衡二叉树是左右两个子树的高度差的绝对值不超过 1。因此一种简单的方法是**选择中点作为根节点，根节点左侧的作为左子树，右侧的作为右子树即可。**原因很简单，这样分配可以保证左右子树的节点数目差不超过 1。因此高度差自然也不会超过 1 了。

上面的操作同时也满足了二叉搜索树，原因就是题目给的数组是有序的。

你也可以选择别的数作为根节点，而不是中点，这也可以看出答案是不唯一的。

代码

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if not nums: return None
        mid = (len(nums) - 1) // 2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid + 1:])
        return root

复杂度分析

• 时间复杂度：由于每个节点最多被访问一次，因此总的时间复杂度为 $O(N)$，其中 $N$ 为数组长度。
• 空间复杂度：由于使用了递归，这里的空间复杂度的瓶颈在栈空间，因此空间复杂度为 $O(h)$，其中 $h$ 为树的高度。同时由于是平衡二叉树，因此 $h$ 就是 $logN$。

109. 有序链表转换二叉搜索树（中等）

题目描述

`给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

思路

和 108 思路一样。 不同的是数据结构的不同，因此我们需要关注的是链表和数组的操作差异。

代码

var sortedListToBST = function (head) {
  if (!head) return null;
  return dfs(head, null);
};

function dfs(head, tail) {
  if (head == tail) return null;
  let fast = head;
  let slow = head;
  while (fast != tail && fast.next != tail) {
    fast = fast.next.next;
    slow = slow.next;
  }
  let root = new TreeNode(slow.val);
  root.left = dfs(head, slow);
  root.right = dfs(slow.next, tail);
  return root;
}

Java Code:

class Solution {
  public TreeNode sortedListToBST(ListNode head) {
      if(head == null) return null;
      return dfs(head,null);
  }
  private TreeNode dfs(ListNode head, ListNode tail){
      if(head == tail) return null;
      ListNode fast = head, slow = head;
      while(fast != tail && fast.next != tail){
          fast = fast.next.next;
          slow = slow.next;
      }
      TreeNode root = new TreeNode(slow.val);
      root.left = dfs(head, slow);
      root.right = dfs(slow.next, tail);
      return root;
  }
}

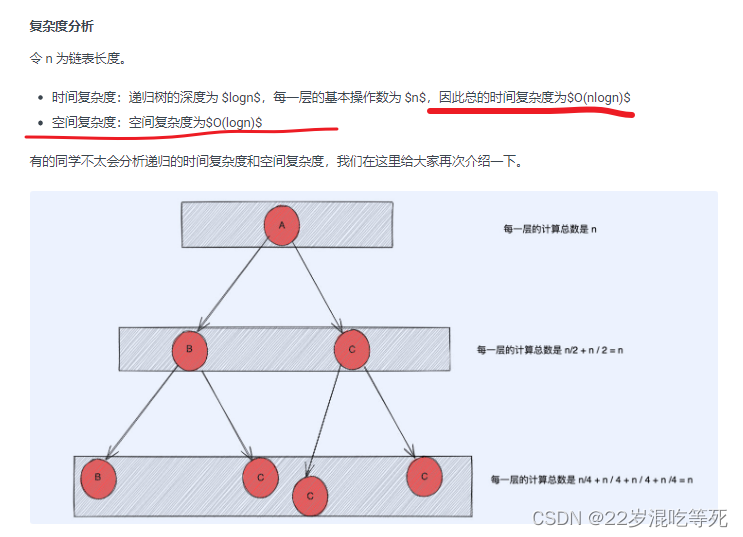
时间复杂度稍微困难一点点。之前西法在先导篇给大家说过：如果有递归那就是：递归树的节点数 * 递归函数内部的基础操作数。而这句话的前提是所有递归函数内部的基本操作数是一样的，这样才能直接乘。而这里递归函数的基本操作数不一样。

不过我们发现递归树内部每一层的基本操作数都是固定的， 为啥固定已经在图上给大家算出来了。因此总的空间复杂度其实可以通过递归深度 * 每一层基础操作数计算得出，也就是 $nlogn$。 类似的技巧可以用于归并排序的复杂度分析中。

另外大家也直接可以通过公式推导得出。对于这道题来说，设基本操作数 T(n)，那么就有 T(n) = T(n/2) * 2 + n/2，推导出来 T(n) 大概是 nlogn。这应该高中的知识。 具体推导过程如下：

1382. 将二叉搜索树变平衡（中等）

题目描述

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

如果有多种构造方法，请你返回任意一种。

 

示例：

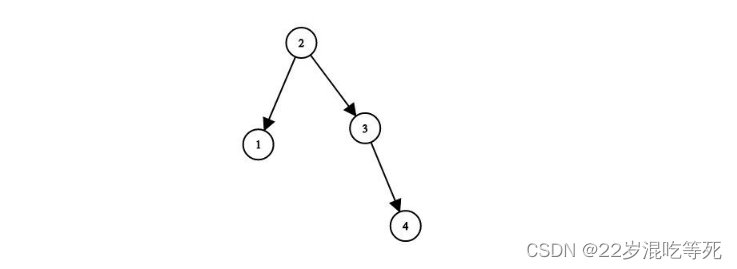
输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。
 

提示：

树节点的数目在 1 到 10^4 之间。
树节点的值互不相同，且在 1 到 10^5 之间。

思路

由于二叉搜索树的中序遍历是一个有序数组，因此问题很容易就转化为 108. 将有序数组转换为二叉搜索树（简单）。

代码

代码支持： Python3
Python3 Code:

class Solution:
    def inorder(self, node):
        if not node: return []
        return self.inorder(node.left) + [node.val] + self.inorder(node.right)
    def balanceBST(self, root: TreeNode) -> TreeNode:
        nums = self.inorder(root)
        def dfs(start, end):
            if start == end: return TreeNode(nums[start])
            if start > end: return None
            mid = (start + end) // 2
            root = TreeNode(nums[mid])
            root.left = dfs(start, mid - 1)
            root.right = dfs(mid + 1, end)
            return root
        return dfs(0, len(nums) - 1)