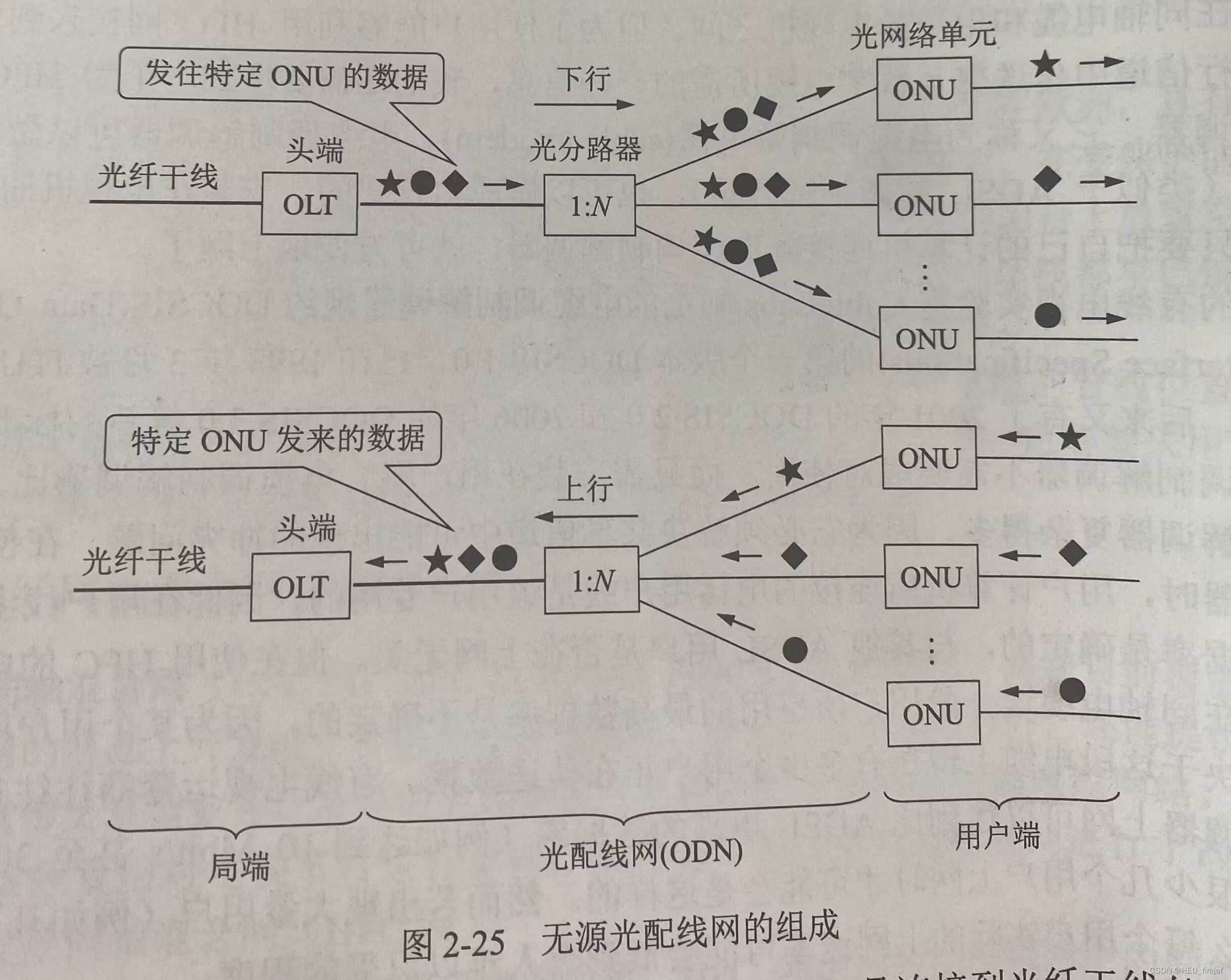
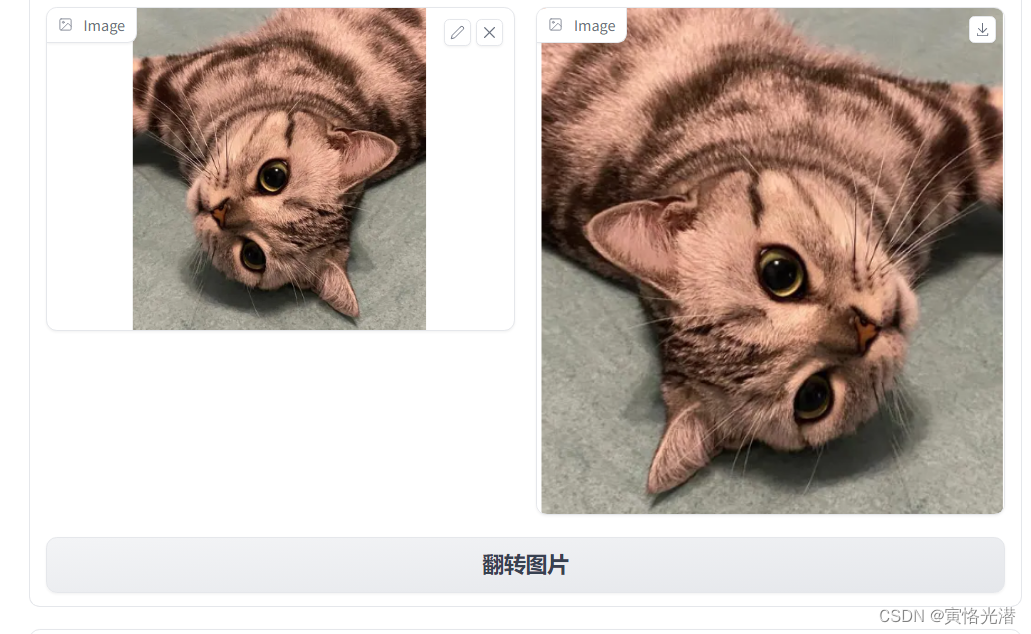
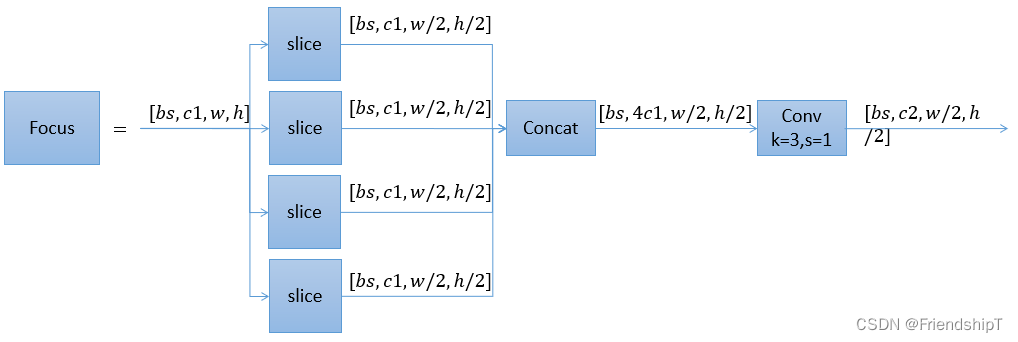
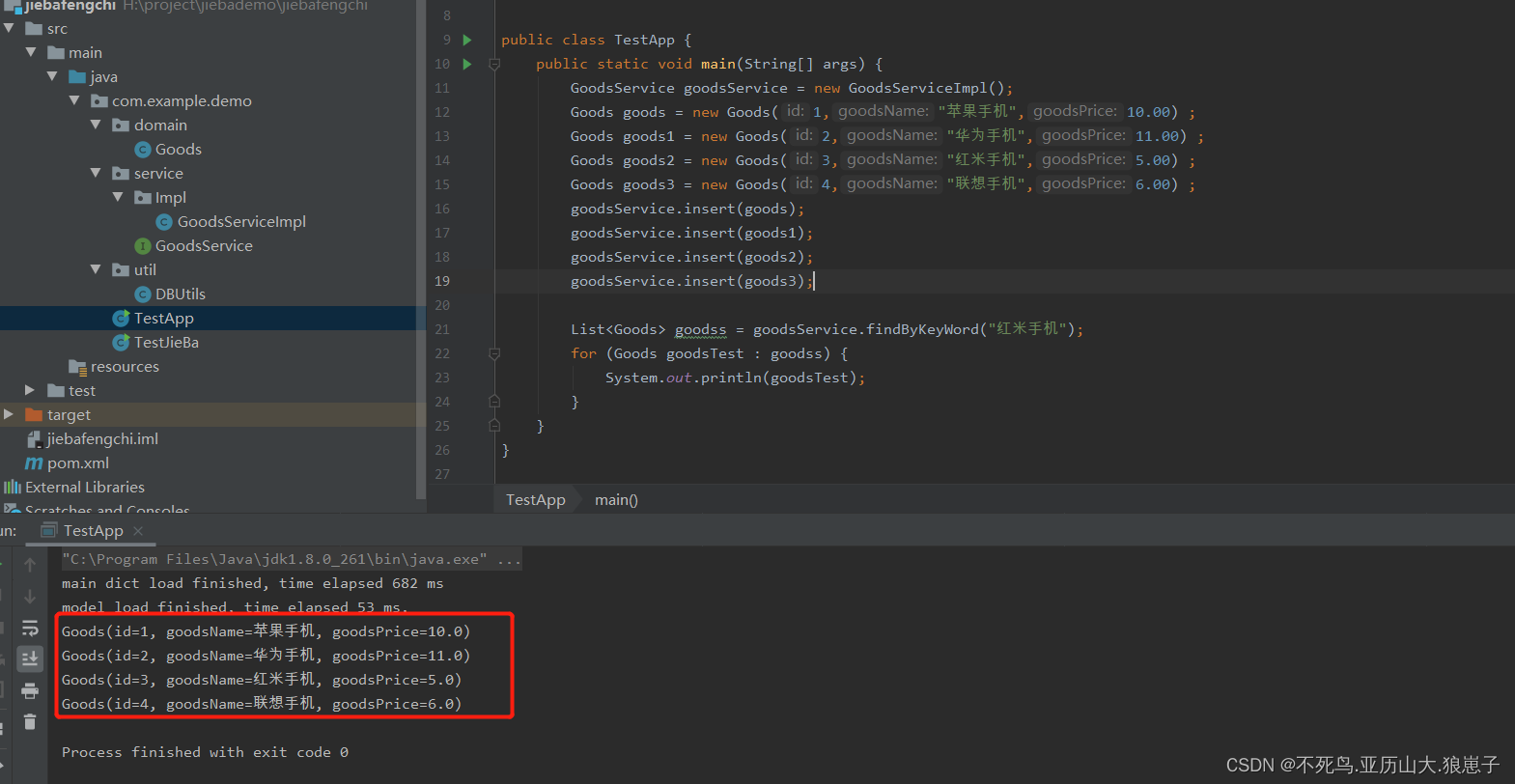
三维变换主要包括:平移、旋转、缩放
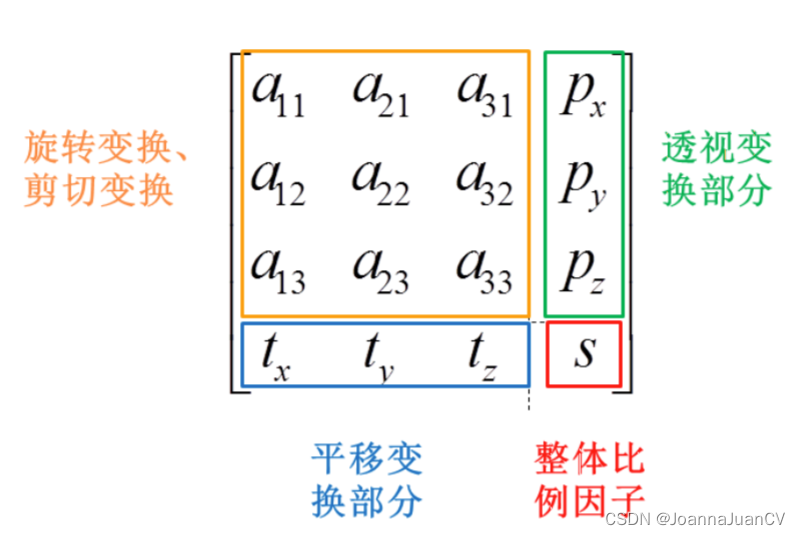
在open3d中,针对三维对象的变换主要有translate、rotate、scale和transform
• Translate 平移
• Rotate 旋转
• Scale 缩放
• Transform 变换矩阵(4*4)
mesh_tx = mesh.translate((1.5, 0, 0))
mesh_r = mesh.rotate(R, center=(0, 0, 0))
mesh_s = mesh.scale(0.5, center=(0, 0, 0))
mesh_t = mesh.transform(T)
三维旋转
Open3d的几何体通过rotate来实现旋转。
它的第一个参数R是一个旋转矩阵,由于3D物体的旋转可以通过多个参数形式来表示,Open3d提供了函数,可以方便的将不同的参数变化为旋转矩阵。
- 使用get_rotation_matrix_from_xyz从欧拉角(Euler angles)转换为矩阵(这里xyz也可以是yzx,zxy,xzy,zyx和yxz);
- 使用get_rotation_matrix_from_axis_angle从轴角(Axis-angle representation)转换;
- 使用get_rotation_matrix_from_quaternion从四元数进行转换;
旋转矩阵
旋转矩阵:用九个数来表示三个自由度,矩阵中的每一列表示旋转后的单位向量方向,缺点是有冗余性,不紧凑。

# 旋转,为便于观察,增加了缩放操作
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame() # 坐标轴
mesh_r = copy.deepcopy(mesh)
R = mesh.get_rotation_matrix_from_xyz((np.pi / 2, 0, np.pi / 4))
mesh_r.rotate(R, center=(0, 0, 0))
mesh_r.scale(0.5, center=mesh_r.get_center())
o3d.visualization.draw_geometries([mesh])
o3d.visualization.draw_geometries([mesh, mesh_r])
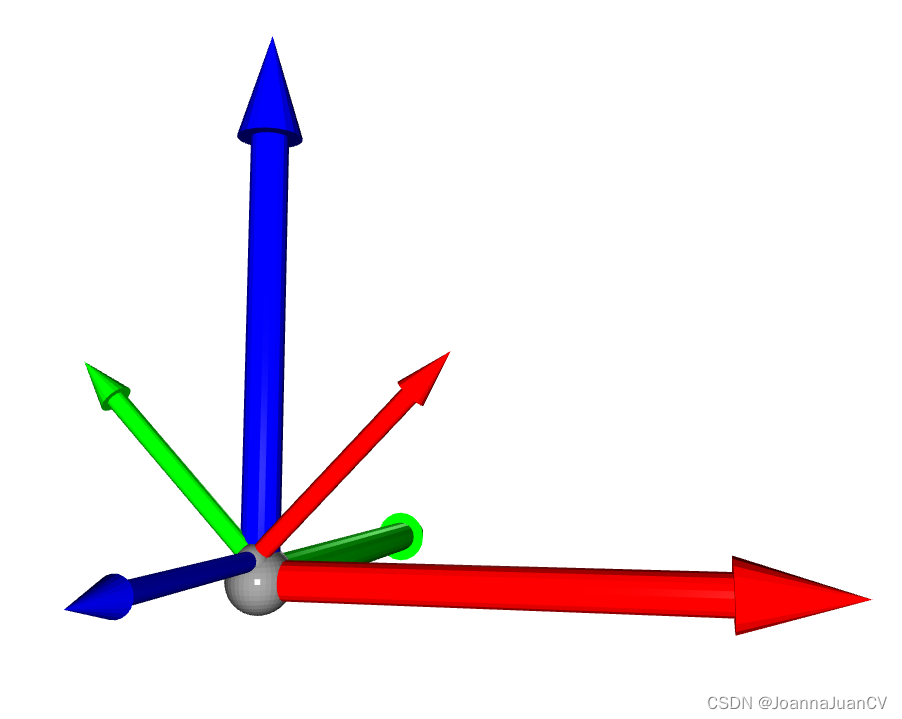
注意:
- 在open3d的三维坐标系中,使用红、绿、蓝三色指代三维坐标轴,分别代表X轴(向前),Y轴(向右)以及Z轴(向上或纸面向外)三个方向;
- 绕X轴逆时针旋转90°, 绕Y轴旋转0°,绕Z轴逆时针旋转45°;
旋转向量
旋转向量:用一个旋转轴和一个旋转角来表示旋转,但是因为周期性,任何2nπ的旋转等价于没有旋转,具有奇异性。
旋转矩阵R,与其对应的旋转向量r,通过下面公式转换:

open3D 接口函数:
open3d.geometry.get_rotation_matrix_from_axis_angle(rotation: numpy.ndarray[numpy.float64[3, 1]]) →
numpy.ndarray[numpy.float64[3, 3]]
欧拉角
欧拉角:将旋转分解为三个分离的转角,常用在飞行器上,但因为万向锁问题(Gimbal Lock) 而同样具有奇异性。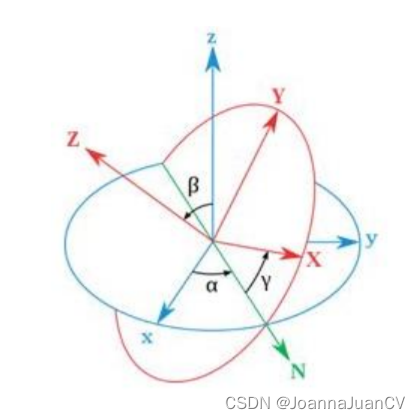
需要区分每次旋转是绕固定轴旋转的,还是绕旋转之后的轴旋转的,使用ZYX(先绕Z再绕Y最后绕X);
逆时针旋转的角度为正时(与右手系旋转方向相同的为旋转正方向),绕不同
轴的旋转结果:

注意:
- 欧拉角的旋转顺序不同,注意乘的顺序
- 坐标系旋转中的左乘——相对于固定坐标系旋转
- 坐标系旋转中的右乘——相对于自身坐标系旋转
open3D 接口函数:
open3d.geometry.get_rotation_matrix_from_xyz(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
open3d.geometry.get_rotation_matrix_from_xzy(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
open3d.geometry.get_rotation_matrix_from_yxz(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
open3d.geometry.get_rotation_matrix_from_yzx(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
open3d.geometry.get_rotation_matrix_from_zxy(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
open3d.geometry.get_rotation_matrix_from_zyx(rotation: numpy.ndarray[numpy.float64[3, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
四元数
四元数:是一种紧凑、易于迭代、又不会出现奇异值的表示方法。它在程序中广为使用,例如ROS和几个著名的SLAM公开数据集、g2o等程序都使用四元数记录机器人的姿态。
四元数是Hamilton找到的一种扩展的复数。一个四元数拥有一个实部和三个虚部
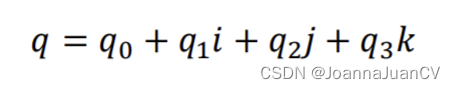
四元数到旋转矩阵:
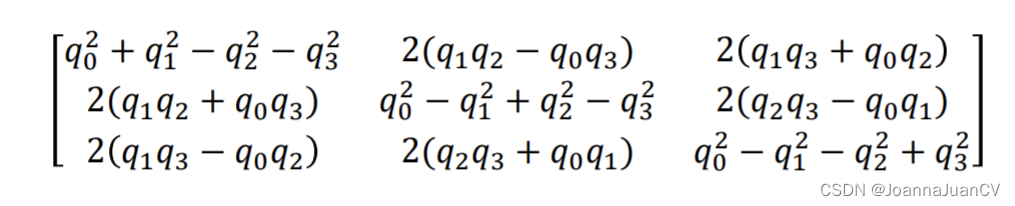
open3D 接口函数:
open3d.geometry.get_rotation_matrix_from_quaternion
(rotation: numpy.ndarray[numpy.float64[4, 1]]) → numpy.ndarray[numpy.float64[3, 3]]
三维平移
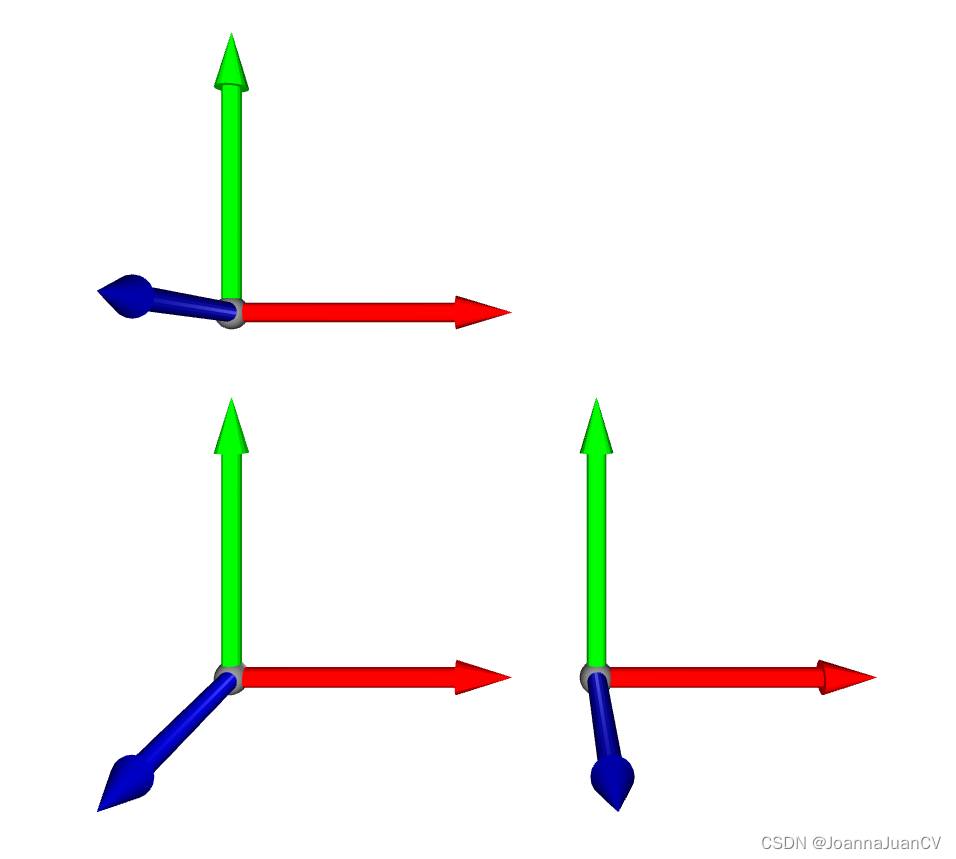
平移算法就是通过单个三维向量 t 来平移所有点/顶点;如下:沿Z轴平移2
# 平移
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
mesh_tx = copy.deepcopy(mesh).translate((1.3, 0, 0)) #位移
mesh_ty = copy.deepcopy(mesh).translate((0, 1.3, 0))
print(f'Center of mesh: {mesh.get_center()}')
print(f'Center of mesh tx: {mesh_tx.get_center()}')
print(f'Center of mesh ty: {mesh_ty.get_center()}')
o3d.visualization.draw_geometries([mesh, mesh_tx, mesh_ty])
Center of mesh: [0.05167549 0.05167549 0.05167549]
Center of mesh tx: [1.35167549 0.05167549 0.05167549]
Center of mesh ty: [0.05167549 1.35167549 0.05167549]
Note:
get_center算法返回的是三角网格顶点的平均值。这就会导致原点在[0,0,0]处的坐标系,使用get_center返回的是[0.05167549
0.05167549 0.05167549]。
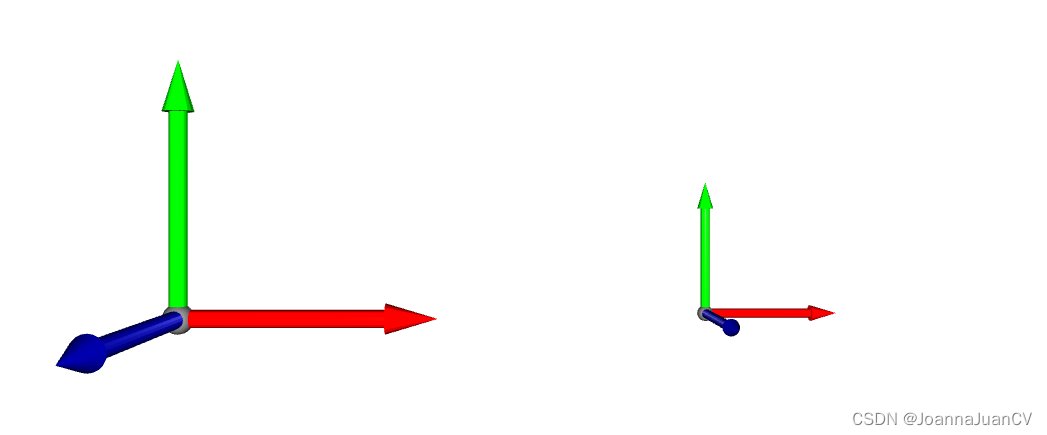
三维缩放
Open3d里面的顶点和点可以应用scale进行缩放:
# 先沿X轴平移,再缩放
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
mesh_s = copy.deepcopy(mesh).translate((2, 0, 0))
mesh_s.scale(0.5, center=mesh_s.get_center())
o3d.visualization.draw_geometries([mesh, mesh_s])
Open3D与numpy互转
Open3D 的数据结构原生兼容NumPy缓冲区;
- Numpy 转 open3d.pointcloud
主要借助Vector3dVector函数,对其进行直接赋值;
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(xyz)
- open3d.PointCloud 转 NumPy
xyz_load = np.asarray(pcd_load.points)