翻译:
Polycarp是伯兰ICPC区域活动的组织者。伯兰有𝑛所大学,编号从1到𝑛。波利卡普认识这个地区所有有竞争力的程序员。有𝑛学生:𝑖-th学生在大学注册𝑢𝑖,有编程技能𝑠𝑖。
Polycarp现在必须决定规则。特别是团队成员的数量。
波利卡普知道,如果他选择团队的规模为某个整数𝑘,每个大学将把他们的𝑘最强(具有最高编程技能的𝑠)的学生派到第一个团队,然后把下一个𝑘最强的学生派到第二个团队,以此类推。如果剩下的学生少于𝑘,那么就不能组建团队。请注意,可能有些大学没有派出任何团队。
该地区的实力是所有参赛队伍成员的技能总和。如果没有队伍在场,那么强度为0。
帮助Polycarp找到每个选择𝑘从1到𝑛的区域的强度。
输入
第一行包含单个整数𝑡(1≤𝑡≤1000)—测试用例的数量。
每个测试用例的第一行包含单个整数𝑛(1≤𝑛≤2⋅105)——大学数量和学生数量。
每个测试用例的第二行包含𝑛整数𝑢1,𝑢2,…,𝑢𝑛(1≤𝑢𝑖≤𝑛)—𝑖-th学生就读的大学。
每个测试用例的第三行包含𝑛整数𝑠1,𝑠2,…,𝑠𝑛(1≤𝑠𝑖≤109)-这是𝑖-th学生的编程技能。
𝑛在所有测试用例上的总和不超过2⋅105。
输出
对于每个测试用例,打印𝑛整数:区域的强度—当前团队成员的总技能—对于每个团队规模的选择𝑘。
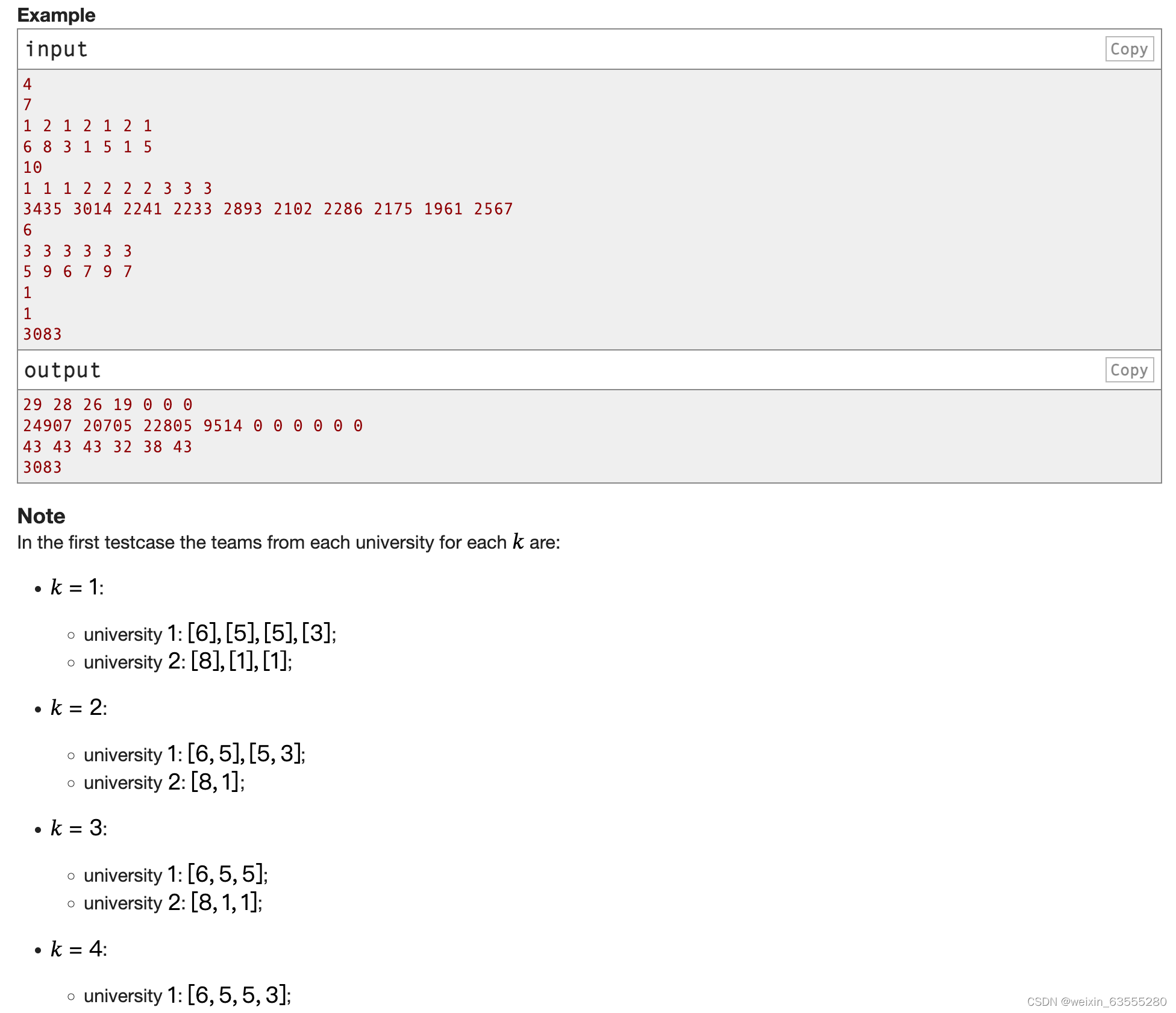
例子
inputCopy
4
7
1 2 1 2 1 2 1 2 1
6 8 3 1 5 1 5
10
1 1 1 2 2 2 2 2 3 3 3
3435 3014 2241 2233 2893 2102 2286 2175 1961 2567
6
3 3 3 3 3 3 3 3 3
5 9 6 7 9 7
1
1
3083
outputCopy
29 28 26 19 0 0
24907 20705 22805 9514 0 0 0 0 0 0 0
43 43 43 32 38 43
3083
请注意
在第一个测试用例中,每个𝑘的每个大学的团队是:
𝑘= 1:
大学1:[6],[5],[5],[3];
大学2:[8],[1],[1];
𝑘= 2:
大学1:[6,5],[5,3];
大学2:[8,1];
𝑘= 3:
大学1:[6,5,5];
大学二:[8,1,1];
𝑘= 4:
大学1:[6,5,5,3];
思路:
每个大学都有不同的人数,强度要最强1~n次询问,所以我们要先预处理出来,让每次查询是O1。我们可以排序,然后用前缀和,来记录每个学校的团队,对于多出来的人,最后取余减一下,就能得出来该学校k个人组成的团队的值。然后我们对学校的数量和人数进行遍历,然后让符合的每个都加上,因为n过大,直接遍历肯定会TLE。
代码:
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long ll;
int n,t;
inline __int128 read(){
__int128 x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9'){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(__int128 x){
if(x < 0){
putchar('-');
x = -x;
}
if(x > 9)
print(x / 10);
putchar(x % 10 + '0');
}
struct we{
int x;
ll y;
}c[200005];
bool cmp(we a,we b){
return a.y>b.y;
}
ll an[200005],jj;
vector<ll>q[200005];
void solv(){
cin>>n;
for (int i =1; i<=n; i++) {
q[i].clear();
q[i].push_back(0);
an[i]=0;
}
int xu=-1;
for (int i =1; i<=n; i++) {
cin>>c[i].x;
xu=max(xu, c[i].x);
}
for (int i =1; i<=n; i++) {
cin>>c[i].y;
}
sort(c+1, c+1+n, cmp);
for (int i =1; i<=n; i++) {
q[c[i].x].push_back(c[i].y+q[c[i].x][q[c[i].x].size()-1]);
}
for (int i =1; i<=n; i++) {
for (int k=1; k<=xu; k++) {
if (q[k].size()<=i) {
continue;
}
if (i==1) {
an[i]+=q[k][q[k].size()-1];
continue;
}
// printf("%d %lld \n",i,an[i]);
// printf("%lld\n",q[k][q[k].size()-q[k].size()%i]);
an[i]+=q[k][q[k].size()-1-(q[k].size()-1)%i];
// printf("%d %lld \n",i,an[i]);
}
printf("%lld ",an[i]);
}printf("\n");
}
int main(){
ios::sync_with_stdio(false);
cin.tie(); cout.tie();
cin>>t;
while (t--) {
solv();
}
return 0;
}