1.集合(set)简介

集合是一种无序可变的容器对象
集合最大的特点:同一个集合内元素是不允许有重复的,因此集合自带"去重"效果

2.集合的定义

集合的定义有两种方式:

• 使用{}进行定义,这种方式不能定义空集合.
• 使用set()进行定义

示例1:

a = {}
b = set()
print(type(a))
print(type(b))

运行截图:

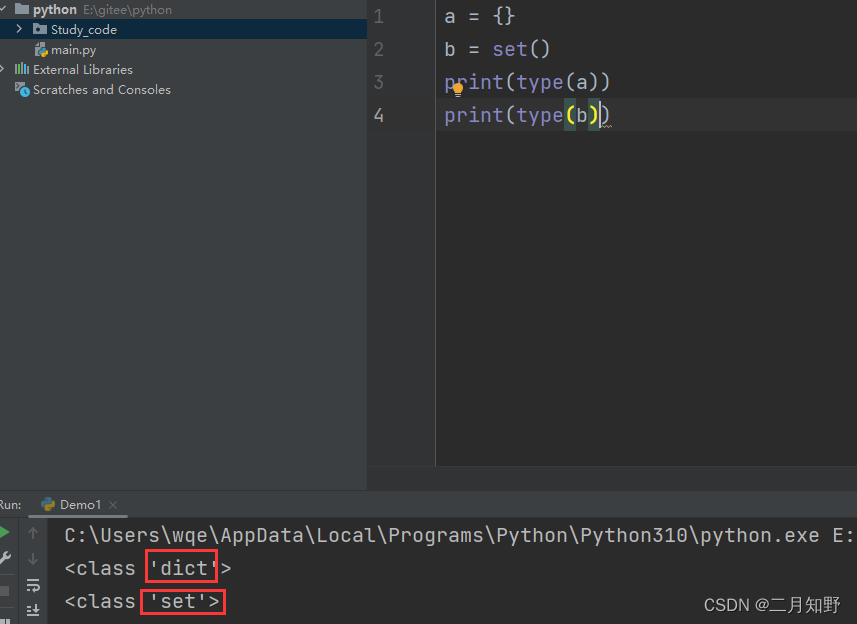
可以看到虽然代码没有报错,但是结果去不一样. a的类型是字典类型,而b的类型才是集合类型. 这是一个需要注意的地方.如果想要定义一个空集合,只能使用set()的方式进行定义.

因为集合中的元素是不能重复的,所以集合具有自动去重的功能.
示例2:

# 自动去重
a = {1, "python", 2.3, 1, "python", 2.3, 1, "python", 2.3, "python"}
print(a)
print(type(a))

# 输出结果:
# {1, 2.3, 'python'}
# <class 'set'>

集合是无序的.注意上面的输出结果的顺序,虽然"python"是在2.3之前的,但是输出时2.3 却在 "python"之前.

集合是不支持下标索引访问 因此集合也没有切片操作.

3.集合的遍历

集合虽然不支持下标索引访问,但是是可以用for循环遍历的

语法: for 临时遍历 in 集合:

a = {1, "python", 2.3}
for elem in a:
    print(elem)
 
# 1
# 2.3
# python

4.集合的常用方法

以下是集合的一些常用方法:

方法	描述
集合.add(元素)	集合内添加一个元素
集合.remove(元素)	删除集合内指定的元素
集合.pop()	从集合内随机取出一个元素
集合.clear()	清除集合
集合1.difference(集合2)	得到一个新的集合,包含两个集合的差集,原集合不变
集合1.difference_update(集合2)	从集合1中删除集合2中存在的元素,集合1改变,集合2不变
集合1.union(集合2)	得到一个新的集合,内含两个集合的所有元素,原集合不变
len(集合)	统计集合中(去重后)元素的个数

感谢你的观看!希望这篇文章能帮到你!
python专栏在不断更新中,欢迎订阅!
“愿与君共勉,携手共进!”