浙大数据结构第四周之二叉搜索树与平衡二叉搜索树（AVL）

news2024/10/6 12:54:18

题目详情：04-树4 是否同一棵二叉搜索树

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。随后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例:

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例:

Yes
No
No

主要思路：

首先建树，依据最初的输入建initialTree,再依次建每个testTree,然后用前序遍历同时遍历initialTree与testTree，来判断这两棵树是否相等

第一次写错误：

建树的插入操作时最后还要返回当前层的root

代码实现：

#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 15
#define SAME 1
#define DIFFERENT 0
#define EMPTY 0
typedef struct {
	bool isEmpty;
    int leftChild;
    int rightChild;
}Node;
Node initialTree[MAX_SIZE];
Node testTree[MAX_SIZE];
int insert(int root,const int num, Node* tree) {
    if(root == EMPTY) return num;

    int leftChildPointer = tree[root].leftChild;
    int rightChildPointer = tree[root].rightChild;
    if(num > root) {
        tree[root].rightChild = insert(rightChildPointer, num, tree);
    }
    else if(num < root) {
        tree[root].leftChild = insert(leftChildPointer, num, tree);
    }
    return root;	//插入关键之一在于最后一步，返回root，这是必不可少的，只有这样才能一级一级向上返回 
}

int buildTree(int* array, Node* tree, int nodeNum) {
    for(int i = 0; i < MAX_SIZE; i++) {
        tree[i].isEmpty = true;
        tree[i].leftChild = EMPTY;
        tree[i].rightChild = EMPTY;
    }
    int root = array[1];
    tree[root].isEmpty = false;
    for(int i = 2; i <= nodeNum; i++) {
        int tmp = array[i];
        tree[tmp].isEmpty = false;
        int noUse = insert(root, tmp, tree);
    }
    return root;
}
int judge(int initialRoot, Node* initialTree, int testRoot, Node* testTree) {
	if(initialRoot == 0 && testRoot == 0) return 1;
	
	if(initialRoot != testRoot) return 0;
	int leftSubTree = judge(initialTree[initialRoot].leftChild, initialTree, testTree[testRoot].leftChild, testTree);
	int rightSubTree = judge(initialTree[initialRoot].rightChild, initialTree, testTree[testRoot].rightChild, testTree);
	if(leftSubTree && rightSubTree) return 1;
	else return 0;
} 
//void printTree(int root, Node* tree) {
//	if(root == 0) return;
//	
//	printf("%d ", root);
//	printTree(tree[root].leftChild, tree);
//	printTree(tree[root].rightChild, tree);
//}
int main() {
    int N, L;
    while(scanf("%d", &N) && (N != 0) && scanf("%d", &L)) {
        int tmp[N];
        for(int i = 1; i <= N; i++) scanf("%d", &tmp[i]);
        int initialRoot = buildTree(tmp, initialTree, N);
//        printTree(initialRoot, initialTree);
//        putchar('\n');
        for(int i = 0; i < L; i++) {
            for(int j = 1; j <= N; j++) {
                scanf("%d", &tmp[j]);
            }
            int testRoot = buildTree(tmp, testTree, N);
//            printTree(testRoot, testTree);
//            putchar('\n');
            if(judge(initialRoot, initialTree, testRoot, testTree)) printf("Yes\n");
            else printf("No\n");
        }
    }
    return 0;
}

题目详情：04-树5 Root of AVL Tree

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

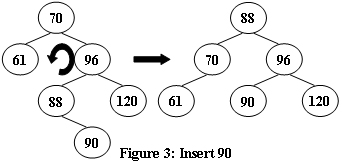
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

简单翻译：

就是给一个二叉平衡树的插入序列，依据这个序列构建二叉平衡树，并返回根节点

主要思路：

用插入法构建，即需要在程序里实现左右单旋与左右双旋

要特别注意的是，如果插入一个节点导致树不平衡了，我们要找到从下往上第一个不平衡的地方进行调整，调整完整个树就平衡了，而不是说要返回到最上面进行调整。

举个列子

假设我们在递归的过程中，输入AVLTree是NULL，也就是如下情况：

 

15这里是一定平衡的（左右都是空），返回给11，11这里肯定也是平衡的，返回给9，但9就不是平衡的了

然后就可以判断让9恢复平衡应该进行哪种操作，即RR还是RL，这里判断为RR。

调整完以后，再返回到9的父节点，这个时候9的父节点再进行判断，以此类推。

第一次写错误：

（1）插入节点进行左旋右旋后对应两个调换位置的节点的高度也要修改
（2）这个问题很隐蔽，首先说明一点，高度是从底往顶计算，从1开始

自己代码

参考代码：

 为什么一个是1一个是0呢？

因为我的代码风格之前跟随了算法训练营，所以理解这题我认为前面部分是终止条件，即遍历到空节点后插入新节点，但忽视了我在插入后直接本轮递归结束返回了，而参考代码还会往下执行一次高度的计算，参考代码虽然建新节点是将高度设为0，但最后还有计算高度，那时叶子节点高度变成1，而我的代码没有执行后面，所以就不能设置高度是0而直接设为1 

就是这个小问题困扰我半天……

代码实现：

#include <stdio.h>
#include <stdlib.h>
typedef struct Node Node;
struct Node {
    int data;
    Node* left;
    Node* right;
    int height;
};
int getMax(int a, int b) {
    return a > b ? a : b;
}
int getTreeHeight(Node* root) {
	int height = 0;
	if(root == NULL) height = 0;
	else height = root -> height;
	return height;
}
Node* singleRightRotation(Node* root) {
    Node* rightSubTree = root -> right;
    root -> right = rightSubTree -> left;
    rightSubTree -> left = root;
    root -> height = getMax(getTreeHeight(root -> left), getTreeHeight(root -> right)) + 1;
    rightSubTree -> height = getMax(getTreeHeight(rightSubTree -> left), root -> height) + 1;
    return rightSubTree;
}
Node* singleLeftRotation(Node* root) {
    Node* leftSubTree = root -> left;
    root -> left = leftSubTree -> right;
    leftSubTree -> right = root;
    root -> height = getMax(getTreeHeight(root -> left), getTreeHeight(root -> right)) + 1;
    leftSubTree -> height = getMax(getTreeHeight(leftSubTree -> left), root -> height) + 1;
    return leftSubTree;	
}
Node* rightLeftRotation(Node* root) {
    root -> right = singleLeftRotation(root -> right);
    return singleRightRotation(root);
}
Node* leftRightRotation(Node* root) {
    root -> left = singleRightRotation(root -> left);
    return singleLeftRotation(root);
}
Node* insert(Node* root, int target) {
    if(root == NULL) {
        root = (Node* )malloc(sizeof(Node));
        root -> data = target;
        root -> left = NULL;
        root -> right = NULL;
        root -> height = 1;
        return root;
    }

	if(target < root -> data) {
        root -> left = insert(root -> left, target);
        if(getTreeHeight(root -> left) - getTreeHeight(root -> right) == 2) {
            if(target < root -> left -> data) {
                root = singleLeftRotation(root);
            }
            else {
                root = leftRightRotation(root);
            }
        }
    }
    
    else if(target > root -> data) {
        root -> right = insert(root -> right, target);
        if(getTreeHeight(root -> right) - getTreeHeight(root -> left) == 2) {
            if(target > root -> right -> data) {
                root = singleRightRotation(root);
            }
            else {
	            root = rightLeftRotation(root);
            }
        }
    }

    root -> height = getMax(getTreeHeight(root -> left), getTreeHeight(root -> right)) + 1;
    return root;
}
void deleteTree(Node* root) {
    if(root == NULL) return;

    deleteTree(root -> left);
    deleteTree(root -> right);
    free(root);
    return;
}
void printTree(Node* root) {
	if(!root) return;
	
	printf("root -> data = %d root -> height = %d\n", root -> data, root -> height);
	
	printTree(root -> left);
	printTree(root -> right);
	return;
}
int main() {
    int N;
    scanf("%d", &N);
    Node* result = NULL;
    for(int i = 0; i < N; i++) {
        int tmp;
        scanf("%d", &tmp);
        result = insert(result, tmp);
    }
//    printTree(result);
    printf("%d", result -> data);
    deleteTree(result);
    return 0;
}

本题参考文章：

树5 Root of AVL Tree

 

题目详情：04-树6 Complete Binary Search Tree

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
  • Both the left and right subtrees must also be binary search trees.

    A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.

    Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.

    Input Specification:

    Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.

    Output Specification:

    For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

    Sample Input:

    10
1 2 3 4 5 6 7 8 9 0

    Sample Output:

    6 3 8 1 5 7 9 0 2 4

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

简单翻译：

给一串构成树的序列，已知该树是完全二叉搜索树，求它的层序遍历的序列

主要思路：

1. 因为二叉搜索树的中序满足：是一组序列的从小到大排列，所以只需将所给序列排序即可得到中序数组in
2. 假设把树按从左到右、从上到下的顺序依次编号，根节点为0，则从根结点root = 0开始中序遍历，root结点的左孩子下标是root*2+1，右孩子下标是root*2+2

递归的终止条件是下标比节点数目大

递归时也按中序遍历

单层处理逻辑是将已知的中序输出结果数组里对应位置的数字赋给通过从0~n -1下标中序遍历的level数组
因为是中序遍历，所以遍历结果与中序数组in中的值从0开始依次递增的结果相同，即in[t++]（t从0开始），将in[t++]赋值给level[root]数组
3. 因为树是按从左到右、从上到下的顺序依次编号的，所以level数组从0到n-1的值即所求的层序遍历的值，输出level数组即可

如下图解释

 

第一次写错误：

第一次直接没思路

代码实现：

#include <stdio.h>
#define MAX_SIZE 2001
int N;
int pointerToIn;
int in[MAX_SIZE];
int level[MAX_SIZE];
void traversal(int root) {
    if(root >= N) return;

    traversal(root * 2 + 1);
    level[root] = in[pointerToIn++];
    traversal(root * 2 + 2);
    return;
}
void sort(int* array, int end) {
    for(int i = 0; i < end; i++) {
        for(int j = i + 1; j < end; j++) {
            if(array[j] < array[i]) {
                int tmp = array[i];
                array[i] = array[j];
                array[j] = tmp;
            }
        }
    }
}
int main() {
    scanf("%d", &N);
    for(int i = 0; i < N; i++) {
        scanf("%d", &in[i]);
    }
    sort(in, N);
    // for(int i = 0; i < N; i++) printf("%d", in[i]);
    // printf("\n");
    pointerToIn = 0;
    traversal(0);
    for(int i = 0; i < N; i++) {
        printf("%d", level[i]);
        if(i < N - 1) printf(" ");
    }
    return 0;
}

参考文章：

题目详情：04-树7 二叉搜索树的操作集

本题要求实现给定二叉搜索树的5种常用操作。

函数接口定义：

BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );

其中BinTree结构定义如下：

typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

 

  • 函数Insert将X插入二叉搜索树BST并返回结果树的根结点指针；
  • 函数Delete将X从二叉搜索树BST中删除，并返回结果树的根结点指针；如果X不在树中，则打印一行Not Found并返回原树的根结点指针；
  • 函数Find在二叉搜索树BST中找到X，返回该结点的指针；如果找不到则返回空指针；
  • 函数FindMin返回二叉搜索树BST中最小元结点的指针；
  • 函数FindMax返回二叉搜索树BST中最大元结点的指针。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

void PreorderTraversal( BinTree BT ); /* 先序遍历，由裁判实现，细节不表 */
void InorderTraversal( BinTree BT );  /* 中序遍历，由裁判实现，细节不表 */

BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );

int main()
{
    BinTree BST, MinP, MaxP, Tmp;
    ElementType X;
    int N, i;

    BST = NULL;
    scanf("%d", &N);
    for ( i=0; i<N; i++ ) {
        scanf("%d", &X);
        BST = Insert(BST, X);
    }
    printf("Preorder:"); PreorderTraversal(BST); printf("\n");
    MinP = FindMin(BST);
    MaxP = FindMax(BST);
    scanf("%d", &N);
    for( i=0; i<N; i++ ) {
        scanf("%d", &X);
        Tmp = Find(BST, X);
        if (Tmp == NULL) printf("%d is not found\n", X);
        else {
            printf("%d is found\n", Tmp->Data);
            if (Tmp==MinP) printf("%d is the smallest key\n", Tmp->Data);
            if (Tmp==MaxP) printf("%d is the largest key\n", Tmp->Data);
        }
    }
    scanf("%d", &N);
    for( i=0; i<N; i++ ) {
        scanf("%d", &X);
        BST = Delete(BST, X);
    }
    printf("Inorder:"); InorderTraversal(BST); printf("\n");

    return 0;
}
/* 你的代码将被嵌在这里 */

输入样例：

10
5 8 6 2 4 1 0 10 9 7
5
6 3 10 0 5
5
5 7 0 10 3

输出样例：

Preorder: 5 2 1 0 4 8 6 7 10 9
6 is found
3 is not found
10 is found
10 is the largest key
0 is found
0 is the smallest key
5 is found
Not Found
Inorder: 1 2 4 6 8 9

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

主要思路：

就是将课本上搜索二叉树增删查的操作实现了一遍

第一次写错误：

（1）二叉搜索树的delete操作时，要考虑待删除节点可能有两个孩子，也可能只有一个孩子或就是叶子节点的情况。

对于节点有两个孩子，转化为删除叶子节点或节点只有一个孩子，在右子树里找到最小值，然后替换，接着就是在右子树里删除最小值节点

代码实现：

BinTree Insert(BinTree BST, ElementType X) {
    if (BST == NULL) {
        BST = (Position)malloc(sizeof(struct TNode));
        BST->Data = X;
        BST->Left = NULL;
        BST->Right = NULL;
        return BST;
    }
    if (X < BST->Data) {  // changed from BST->Data < X
        BST->Left = Insert(BST->Left, X);
    }
    else if (X > BST->Data) {  // changed from BST->Data > X
        BST->Right = Insert(BST->Right, X);
    }
    // else case is not needed, since X already exists in the BST
    return BST;
}

BinTree Delete(BinTree BST, ElementType X) {
    if(BST == NULL) {
        printf("Not Found\n");
        return BST;
    }

    if(X < BST -> Data) {
        BST -> Left = Delete(BST -> Left, X);
    }
    else if(X > BST -> Data){
        BST -> Right = Delete(BST -> Right, X);
    }
    else {
        Position tmp;
        BinTree leftSubtree = BST -> Left;
        BinTree rightSubtree = BST -> Right;
        if(leftSubtree && rightSubtree) {
            tmp = FindMin(rightSubtree);
            BST -> Data = tmp -> Data;
            rightSubtree = Delete(rightSubtree, tmp -> Data);
        }
        else {
            tmp = BST;
            if(leftSubtree == NULL) {
                BST = rightSubtree;
            }
            else {
                BST = leftSubtree;
            }
            free(tmp);
        }
    }
    return BST;
}
Position Find(BinTree BST, ElementType X) {
    if (BST == NULL) {
        return NULL;
    }
    if (X < BST->Data) {
        return Find(BST->Left, X);
    }
    else if (X > BST->Data) {
        return Find(BST->Right, X);
    }
    else {
        return BST;
    }
}

Position FindMin(BinTree BST) {
    if (BST == NULL) {
        return NULL;
    }
    if (BST->Left == NULL) {
        return BST;
    }
    else {
        return FindMin(BST->Left);
    }
}

Position FindMax(BinTree BST) {
    if (BST == NULL) {
        return NULL;
    }
    if (BST->Right == NULL) {
        return BST;
    }
    else {
        return FindMax(BST->Right);
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496246.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Python系列】一个简单的抽奖小程序

【Python系列】一个简单的抽奖小程序

序言 很开心你能在万千博文中打开这一篇&#xff0c;希望能给你带来一定的帮助&#xff01;&#x1f44d;&#x1f3fb; 如果有什么问题&#xff0c;都可以添加下方我的联系方式&#xff0c;联系我噢~&#x1f601; ⭐️⭐️⭐️⭐️⭐️沟通交流&#xff0c;一起成为技术达人&…
阅读更多...
SpringMVC底层原理源码解析

SpringMVC底层原理源码解析

SpringMVC的作用毋庸置疑&#xff0c;虽然我们现在都是用SpringBoot&#xff0c;但是SpringBoot中仍然是在使用SpringMVC来处理请求。 我们在使用SpringMVC时&#xff0c;传统的方式是通过定义web.xml&#xff0c;比如&#xff1a; <web-app><servlet><servle…
阅读更多...
jenkins配置笔记

jenkins配置笔记

文章目录 1.装Gogs插件2.配置截图及说明3.其他1.装Gogs插件 Gogs 插件是一个专门为集成 Gogs（一种类似于 Git 的开源版本控制系统）与 Jenkins 进行交互的插件。它允许 Jenkins 与 Gogs 之间进行双向通信，提高了 Jenkins 对于代码管理和构建的支持。 2.配置截图及说明 目前…
阅读更多...
【操作系统】第二章进程与线程、处理机调度与调度算法

【操作系统】第二章进程与线程、处理机调度与调度算法

文章目录 &#x1f337; 一、进程的定义、组成、组织方式及特征⭐️ 1、 进程的定义⭐️ 2、 进程实体的组成⭐️ 3、 进程的组织⭐️ 4、 进程的特征 &#x1f337; 二、进程的状态与转换⭐️ 1、 状态⭐️ 2、 进程状态间的转换 &#x1f337; 三、进程控制⭐️ 1、 定义⭐️…
阅读更多...
SwiftUI 新 Alert 弹出窗口圆你文本输入之梦

SwiftUI 新 Alert 弹出窗口圆你文本输入之梦

概览 小伙伴们都知道&#xff0c;弹出 Alert 不能包含文本输入框是 SwiftUI 的阿喀琉斯之踵(Achilles’ Heel) 。当然&#xff0c;这说的有些夸张了。&#x1f609; 不过&#xff0c;Alert 不能包含 TextField 在某些情况下着实不方便。于是乎&#xff0c;从 SwiftUI 3.0&…
阅读更多...
JAVA模拟堆

JAVA模拟堆

堆的性质 堆是一种特殊的树。 只要满足以下两点&#xff0c;它就是一个堆&#xff1a; 堆是一个完全二叉树。堆中每一个节点的值都必须大于等于&#xff08;或小于等于&#xff09;其子树中每个节点的值。 第一点&#xff0c;堆必须是一个完全二叉树。完全二叉树要求&#…
阅读更多...
O2OA (翱途) 平台 V8.0 发布新增数据台账能力

O2OA (翱途) 平台 V8.0 发布新增数据台账能力

亲爱的小伙伴们&#xff0c;O2OA (翱途) 平台开发团队经过几个月的持续努力&#xff0c;实现功能的新增、优化以及问题的修复。2023 年度 V8.0 版本已正式发布。欢迎大家到 O2OA 的官网上下载进行体验&#xff0c;也希望大家在藕粉社区里多提宝贵建议。本篇我们先为大家介绍应用…
阅读更多...
Android 输入系统

Android 输入系统

概述 Android 输入系统的工作原理概括来说&#xff0c;内核将原始事件写入到设备节点中&#xff0c;InputReader 不断地通过 EventHub 将原始事件取出来并翻译加工成 Android 输入事件&#xff0c;然后交给 InputDispatcher。 InputDispatcher 根据 WMS 提供的窗口信息将事件…
阅读更多...
24.Stream流

24.Stream流

Stream流 一、什么是Stream流 Stream流操作是Java 8提供一个重要新特性&#xff0c;它允许开发人员以声明性方式处理集合&#xff0c;其核心类库主要改进了对集合类的 API和新增Stream操作。Stream类中每一个方法都对应集合上的一种操作。将真正的函数式编程引入到Java中&…
阅读更多...
2023全栈开发人员职业路线图

2023全栈开发人员职业路线图

0. 全栈开发人员职业路线图 全栈开发人员是IT行业中薪资最高的职业之一。 如果您想成为一名全栈开发人员&#xff0c;以下是2023年全栈开发人员路线图上的十一个步骤&#xff1a; 掌握敏捷开发和Scrum学习浏览器技术&#xff0c;如HTML和CSS熟练掌握JavaScript或TypeScript了…
阅读更多...
单月涨粉303.72w，反差感才是主流吗？

单月涨粉303.72w，反差感才是主流吗？

据新抖「直播带货风向」数据显示&#xff0c;抖音4月的直播商品数量达到1021.32w&#xff0c;较上月的695.91w环比增长50.18%&#xff0c;直播销量环比增加16.81%。从这几个数值就可以看出4月的抖音电商依旧如火如荼...... 那么&#xff0c;4月&#xff0c;抖音又出现哪些新的看…
阅读更多...
“世界中医药之都” 亳州市医保局领导一行莅临万民健康交流指导

“世界中医药之都” 亳州市医保局领导一行莅临万民健康交流指导

为进一步推进智慧医疗、智慧服务、智慧管理“三位一体”为主旨的“智慧中医、健康社区”项目建设。2023 年 5 月 3 日&#xff0c;“世界中医药之都” 亳州市医保局 局长 吴旭春 、 医保中心主任秦克靖 、 办公室主任徐伟 等一行 5 人莅临 万民健康交流 指导工作 &#xff0c…
阅读更多...
day27_mysql

day27_mysql

今日内容 零、 复习昨日 一、单表查询 二、多表联查 零、 复习昨日 1 DDL,DML,DQL是啥 DDL 数据定义语言&#xff08;库&#xff0c;表&#xff0c;列&#xff09;DML 数据操作语言&#xff08;表内数据的操作增删改&#xff09;DQL 数据查询语言&#xff08;表内数据的查询&am…
阅读更多...
酷游浅谈网站Javas cript型别

酷游浅谈网站Javas cript型别

最近整理了一下&#xff0c;【酷游娜娜手机&#x1d54d;找看看nay3989提供】就决定跟大家讨论一下最近对于Javascripet的型别认识。 弱型别&#xff36;&#xff33; 强型别 Javascripet是一种「弱型别」的语言&#xff0c;所以会产生很多你意想不到恶心的事情 至于什么是弱…
阅读更多...
软件测试、测试和开发、测试和调试【详细介绍】

软件测试、测试和开发、测试和调试【详细介绍】

目录 一、什么是软件测试 1.软件测试的定义 2.软件测试的目的 3.软件测试的不可穷性 二、开发和测试的区别 三、测试和调试的区别 一、什么是软件测试 在日常生活中&#xff0c;测试是无处不在的。比如新买的手机是否好用、新买的衣服穿着是否合身等等场景&#xff0c;均…
阅读更多...
点成案例丨细胞培养芯片用于构建肠模型实例分享

点成案例丨细胞培养芯片用于构建肠模型实例分享

器官芯片是一种利用微芯片制造技术制造的微流体细胞培养设备。该设备包含多个连续灌注腔室&#xff0c;具有多细胞层结构、组织界面、物理化学微环境以及人体血管循环等特征&#xff0c;可以模拟和重构人体器官的生理功能&#xff0c;为相关研究提供了可靠的平台。器官芯片技术…
阅读更多...
java中设计模式总结

java中设计模式总结

设计模式是实际工作中写的各种代码进行高层次抽象的总结&#xff0c;其中最出名的当属 Gang of Four (GoF) 的分类了&#xff0c;他们将设计模式分类为 23 种经典的模式&#xff0c;根据用途又可以分为三大类&#xff0c;分别为创建型模式、结构型模式和行为型模式。 有一些重…
阅读更多...
【6D位姿估计】Point Pair Feature (PPF)

【6D位姿估计】Point Pair Feature (PPF)

论文链接：Drost et al. Model Globally, Match Locally: Efficient and Robust 3D Object Recognition. CVPR, 2010. Model Globally, Match Locally 论文名字用 4 个词高度总结了 PPF 算法的精髓：“整体建模，局部匹配”。 下面这张图反应了论文的基本思想（算法概要）： …
阅读更多...
【鸿蒙应用ArkTS开发系列】- 导航栏Tab组件使用讲解

【鸿蒙应用ArkTS开发系列】- 导航栏Tab组件使用讲解

目录 Tabs介绍Tabs使用例子TabBar 样式设置定义菜单样式对象-NavigationItem定义一个底部菜单栏集合数据-NavigationList修改TabBuilder Tab 组件控制题外话 现在市场上的大部分应用&#xff0c;主页都是才用底部导航栏菜单作为页面主体框架来展示&#xff0c; 在鸿蒙中是使用…
阅读更多...
STM32库函数笔记分享

STM32库函数笔记分享

之前刚开始自学的部分STM32笔记放出&#xff0c;希望对新入门STM32和想要复习库函数的小伙伴们起到帮助。 建立工程 1.寄存器操作方式 需要不断地查手册来了解每一位是干什么用的 优点&#xff1a;代码简介&#xff1b; 缺点&#xff1a;不太方便。 2.库函数操作方式 1.调用库函…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023