背景
相信大家都玩过下面的迷宫游戏。你的目标是从地图的某一个角落移动到地图的出口。规则很简单,仅仅你不能穿过墙。

实际上,这道题并不能够使用并查集来解决。 不过如果我将规则变成,“是否存在一条从入口到出口的路径”,那么这就是一个简单的联通问题,这样就可以借助本节要讲的并查集来完成。
另外如果地图不变,而不断改变入口和出口的位置,并依次让你判断起点和终点是否联通,并查集的效果高的超出你的想象。
另外并查集还可以在人工智能中用作图像人脸识别。比如将同一个人的不同角度,不同表情的面部数据进行联通。这样就可以很容易地回答两张图片是否是同一个人,无论拍摄角度和面部表情如何。
概述
并查集使用的是一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。
比如让你求两个人是否间接认识,两个地点之间是否有至少一条路径。
上面的例子其实都可以抽象为联通性问题。
即如果两个点联通,那么这两个点就有至少一条路径能够将其连接起来。值得注意的是,并查集只能回答“联通与否”,而不能回答诸如“具体的联通路径是什么”。
如果要回答“具体的联通路径是什么”这个问题,则需要借助其他算法,比如广度优先遍历。
形象解释
比如有两个司令。 司令下有若干军长,军长下有若干师长。。。
判断两个节点是否联通
我们如何判断某两个师长是否归同一个司令管呢(连通性)?
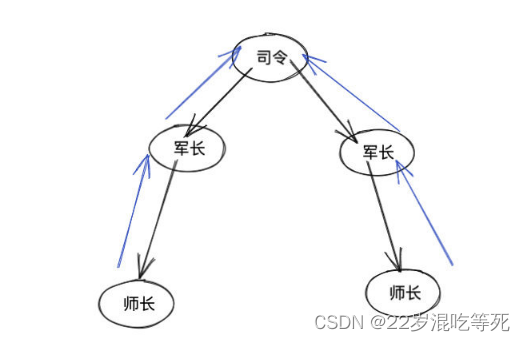
很简单,我们顺着师长,往上找,找到司令。 如果两个师长找到的是同一个司令,那么两个人就归同一个司令管。(假设这两人级别比司令低)
如果我让你判断两个士兵是否归同一个师长管,也可以向上搜索到师长,如果搜索到的两个师长是同一个,那就说明这两个士兵归同一师长管。(假设这两人级别比师长低)
代码上我们可以用 parent[x] = y 表示 x 的 parent 是 y,通过不断沿着搜索 parent 搜索找到 root,然后比较 root 是否相同即可得出结论。 这里的 root 实际上就是上文提到的集合代表。
之所以使用 parent 存储每个节点的父节点,而不是使用 children 存储每个节点的子节点是因为“我们需要找到某个元素的代表(也就是根)”
这个不断往上找的操作,我们一般称为 find,使用 ta 我们可以很容易地求出两个节点是否连通。
合并两个联通区域

我们将其合并为一个联通域,最简单的方式就是直接将其中一个司令指向另外一个即可:
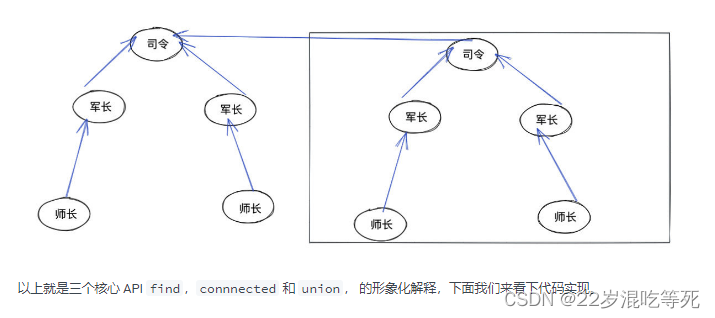
核心 API
并查集(Union-find Algorithm)定义了两个用于此数据结构的操作:
- Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合。
首先我们初始化每一个点都是一个连通域,类似下图:

为了更加精确的定义这些方法,需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素,称为代表,以表示整个集合。接着,Find(x) 返回 x 所属集合的代表,而 Union 使用两个集合的代表作为参数进行合并。初始时,每个人的代表都是自己本身。
这里的代表就是上面的“司令”。
比如我们的 parent 长这个样子:
{
"0": "1",
"1": "3",
"2": "3",
"4": "3",
"3": "3"
}
find
假如我让你在上面的 parent 中找 0 的代表如何找?
首先,树的根在 parent 中满足“parent[x] == x”。因此我们可以先找到 0 的父亲 parent[0] 也就是 1,接下来我们看 1 的父亲 parent[1] 发现是 3,因此它不是根,我们继续找 3 的父亲,发现是 3 本身。也就是说 3 就是我们要找的代表,我们返回 3 即可。
递归:
def find(self, x):
while x != self.parent[x]:
x = self.parent[x]
return x
迭代:
也可使用递归来实现。
def find(self, x):
if x != self.parent[x]:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
return x
这里我在递归实现的 find 过程进行了路径的压缩,每次往上查找之后都会将树的高度降低到 2。
这有什么用呢?我们知道每次 find 都会从当前节点往上不断搜索,直到到达根节点,因此 find 的时间复杂度大致相等于节点的深度,树的高度如果不加控制则可能为节点数,因此 find 的时间复杂度可能会退化到 O ( n ) O(n) O(n)。而如果进行路径压缩,那么树的平均高度不会超过 l o g n logn logn,如果使用了路径压缩和下面要讲的按秩合并那么时间复杂度可以趋近 O ( 1 ) O(1) O(1),具体证明略。不过给大家画了一个图来辅助大家理解。
注意是趋近 O(1),准确来说是阿克曼函数的某个反函数。
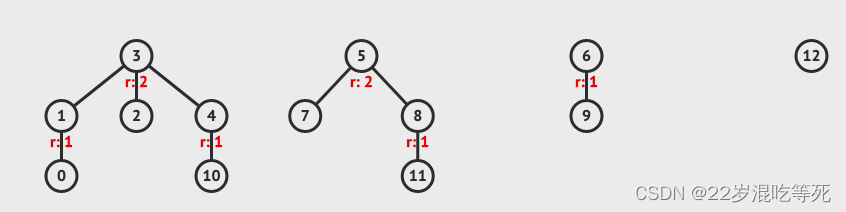
极限情况下,每一个路径都会被压缩,这种情况下继续查找的时间复杂度就是 O ( 1 ) O(1) O(1)。

connected
直接利用上面实现好的 find 方法即可。如果两个节点的祖先相同,那么其就联通。
def connected(self, p, q):
return self.find(p) == self.find(q)
union
将其中一个节点挂到另外一个节点的祖先上,这样两者祖先就一样了。也就是说,两个节点联通了。
对于如下的一个图:

如果我们将 0 和 7 进行一次合并。即 union(0, 7) ,则会发生如下过程。
- 找到 0 的根节点 3
- 找到 7 的根节点 6
- 将 6 指向 3。(为了使得合并之后的树尽可能平衡,一般选择将小树挂载到大树上面,下面的代码模板会体现这一点。3 的秩比 6 的秩大,这样更利于树的平衡,避免出现极端的情况)
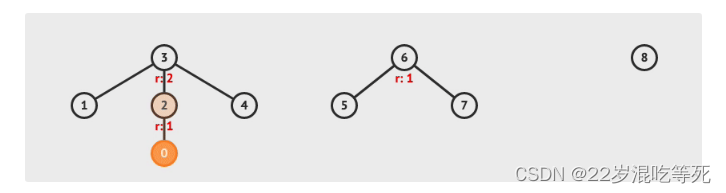
上面讲的小树挂大树就是所谓的按秩合并。
代码:
def union(self, p, q):
if self.connected(p, q): return
self.parent[self.find(p)] = self.find(q)
这里我并没有判断秩的大小关系,目的是方便大家理清主脉络。完整代码见下面代码区。
不带权并查集
平时做题过程,遇到的更多的是不带权的并查集。相比于带权并查集, 其实现过程也更加简单。
代码模板
class UF:
def __init__(self, M):
self.parent = {}
self.size = {}
self.cnt = 0
# 初始化 parent,size 和 cnt
# size 是一个哈希表,记录每一个联通域的大小,其中 key 是联通域的根,value 是联通域的大小
# cnt 是整数,表示一共有多少个联通域
for i in range(M):
self.parent[i] = i
self.cnt += 1
self.size[i] = 1
def find(self, x):
if x != self.parent[x]:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
return x
def union(self, p, q):
if self.connected(p, q): return
# 小的树挂到大的树上, 使树尽量平衡
leader_p = self.find(p)
leader_q = self.find(q)
if self.size[leader_p] < self.size[leader_q]:
self.parent[leader_p] = leader_q
self.size[leader_q] += self.size[leader_p]
else:
self.parent[leader_q] = leader_p
self.size[leader_p] += self.size[leader_q]
self.cnt -= 1
def connected(self, p, q):
return self.find(p) == self.find(q)
带权并查集
上面讲到的其实都是有向无权图,因此仅仅使用 parent 表示节点关系就可以了。而如果使用的是有向带权图呢?实际上除了维护 parent 这样的节点指向关系,我们还需要维护节点的权重,一个简单的想法是使用另外一个哈希表 weight 存储节点的权重关系。比如 weight[a] = 1 表示 a 到其父节点的权重是 1。
如果是带权的并查集,其查询过程的路径压缩以及合并过程会略有不同,因为我们不仅关心节点指向的变更,也关心权重如何更新。比如:

代码模板
这里以加法型带权并查集为例,讲述一下代码应该如何书写。
class UF:
def __init__(self, M):
# 初始化 parent,weight
self.parent = {}
self.weight = {}
for i in range(M):
self.parent[i] = i
self.weight[i] = 0
def find(self, x):
if self.parent[x] != x:
ancestor, w = self.find(self.parent[x])
self.parent[x] = ancestor
self.weight[x] += w
return self.parent[x], self.weight[x]
def union(self, p, q, dist):
if self.connected(p, q): return
leader_p, w_p = self.find(p)
leader_q, w_q = self.find(q)
self.parent[leader_p] = leader_q
self.weight[leader_p] = dist + w_q - w_p
def connected(self, p, q):
return self.find(p)[0] == self.find(q)[0]

复杂度分析
令 n 为图中点的个数。
首先分析空间复杂度。空间上,由于我们需要存储 parent (带权并查集还有 weight) ,因此空间复杂度取决于于图中的点的个数, 空间复杂度不难得出为 O ( n ) O(n) O(n)。
并查集的时间消耗主要是 union 和 find 操作,路径压缩和按秩合并优化后的时间复杂度接近于 O(1)。更加严谨的表达是 O(log(m×Alpha(n))),n 为合并的次数, m 为查找的次数,这里 Alpha 是 Ackerman 函数的某个反函数。但如果只有路径压缩或者只有按秩合并,两者时间复杂度为 O(logx)和 O(logy),x 和 y 分别为合并与查找的次数。
应用
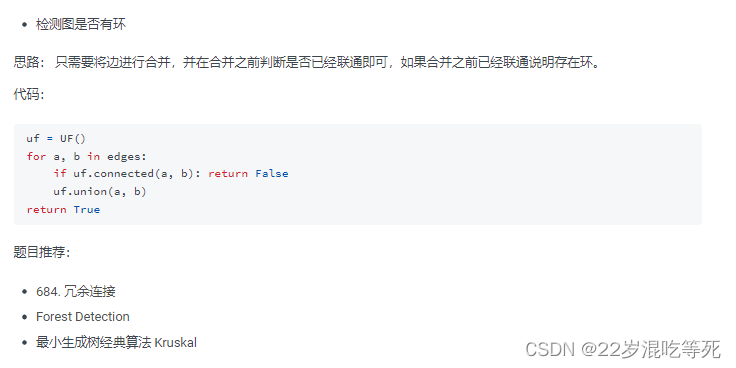
练习