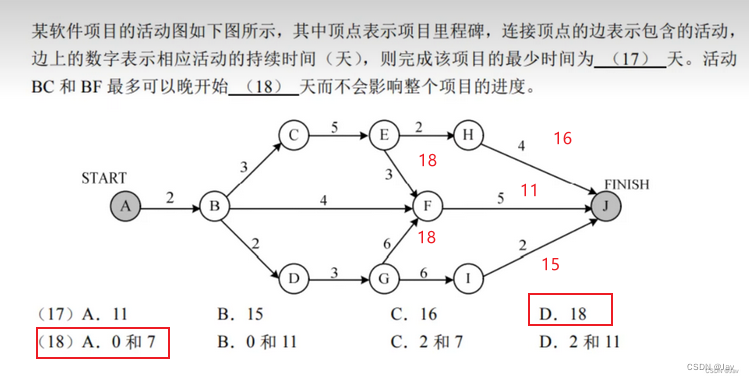
题目描述

给定一个二维平面及平面上的 N 个点列表Points，其中第i个点的坐标为Points[i]=[Xi,Yi]。请找出一条直线，其通过的点的数目最多。

设穿过最多点的直线所穿过的全部点编号从小到大排序的列表为S，你仅需返回[S[0],S[1]]作为答案，若有多条直线穿过了相同数量的点，则选择S[0]值较小的直线返回，S[0]相同则选择S[1]值较小的直线返回。

示例：

输入： [[0,0],[1,1],[1,0],[2,0]]
输出： [0,2]
解释： 所求直线穿过的3个点的编号为[0,2,3]

提示：

2 <= len(Points) <= 300
len(Points[i]) = 2

解题思路与代码

这道题又是一道关于数学几何问题的题目，考察到了同学们对向量知识的了解。如何通过向量来判断3点共线问题。

如果大家的几何数学知识好的话，这道题确实不算一道难题。就直接先来给大家普及一下向量的知识吧。
- 假如点A，点B两点构成一条直线，我们可以用向量a去表示这条直线。那么a这个向量坐标我们可以记为（x1，y1）x1 = xB - xA， y1 = yB - yA
- 假如点A，点C两点构成一条直线，我们可以用向量a去表示这条直线。那么b这个向量坐标我们可以记为（x2，y2）x2 = xC - xA， y2 = yC - yA
- 如果直线AC与直线AB是同一条直线了话，向量a - 向量b = 0；根据向量的运算法则，也就是说，x2y1 - x1y2 = 0；
- OK，直到这么多关于向量的知识就可以了。我们就可以来解决这道题了。
对于这道题，我们需要先创建一个vector（result）来存储最后的答案，两个int（maxCount，count）来去记录遍历中一条直线穿过最多节点的个数。
之后用双层for循环固定两个点，也就是一个向量，第三层for循环再固定一个点，与第一个点凑成第二个向量
第三层for循环就是用来循环比较一条直线上有多少个点的。如果有，我们就加入count，第三层循环完毕后，更新maxcount，result的值。
最后我们可以进行一个剪枝操作，也就是points.size()- 1 - j + 2 <= maxcount。
- points.size() - 1 - j表示从当前点j开始到最后一个点之间的点的数量。加2是因为我们还要考虑初始的两个点i和j。
最后返回result，我们这道题就算是彻底做完啦！

具体的代码如下：

class Solution {
public:
    vector<int> bestLine(vector<vector<int>>& points) {
        vector<int> result(2);
        int maxcount = 0;
        int count = 0;
        for(int i = 0; i < points.size() - 1; ++i){
            for(int j = i + 1; j < points.size(); ++j){
                if(points.size()- 1 - j + 2 <= maxcount) break;
                long long x1 = points[j][0] - points[i][0];
                long long y1 = points[j][1] - points[i][1];
                count = 2;
                for(int k = j + 1; k < points.size(); ++k){
                    long long x2 = points[k][0] - points[i][0];
                    long long y2 = points[k][1] - points[i][1];
                    if(x1 * y2 == x2 * y1) ++count;
                }
                if(count > maxcount){
                    maxcount = count;
                    result[0] = i;
                    result[1] = j;
                }
            }
        }
        return result;
    }
};