文章目录
- 如何求一个中位数?
- [295. 数据流的中位数](https://leetcode.cn/problems/find-median-from-data-stream/)
- 常规思路:
- 解决思路:
如何求一个中位数?
如果输入一个数组,让你求中位数,简单的解决方法就是对数组进行排序
如果数组长度是奇数,最中间的一个元素就是中位数
如果数组长度是偶数,最中间两个元素的平均数作为中位数。
但是如果数据规模非常巨大,排序不太现实,那么也可以使用概率算法,随机抽取一部分数据,排序,求中位数,作为所有数据的中位数。
295. 数据流的中位数
这道题就是让我们设计这样一个类:
class MedianFinder {
// 添加一个数字
public void addNum(int num) {}
// 计算当前添加的所有数字的中位数
public double findMedian() {}
}
常规思路:
常规的思路就是
用一个数组记录所有addNum添加进来的数字,通过插入排序的逻辑保证数组中的元素有序,当调用findMedian方法时,可以通过数组索引直接计算中位数
但是用数组作为底层容器的问题也很明显:
addNum搜索插入位置的时候可以用二分搜索算法,但是插入操作需要搬移数据,最坏时间复杂度为O(N)
因为数组的插入时间复杂度问题,考虑使用链表。
使用链表插入数据很快,但是查找插入位置的时候只能线性遍历,最坏时间复杂度为 O(N)
而且findMedian方法也需要遍历寻找中间索引,最坏时间复杂度也是 O(N)
因为链表的查找时间复杂度问题,考虑使用平衡二叉树
平衡二叉树的增删查改的复杂度都为 O(logN)
比如使用Java提供的TreeSet容器,底层是红黑树,addNum直接插入,findMedian可以通过当前元素的个数推算出计算中位数元素的排名
但是,TreeSet是一种Set其中不存在重复元素的元素,但是我们的数据流可能输入重复数据,而且计算中位数也是需要算上重复元素的
不仅如此,TreeSet并没有实现一个通过排名快速计算元素的API。也就是说加入我们想找到TreeSet中的第5大的元素我们需要手动去实现这个需求
平衡二叉树也不行,那**优先级队列(二叉堆)**可以吗?
优先级队列是一种受限的数据结构,只能从堆顶添加/删除元素,我们的addNum方法可以从堆顶插入元素,但是findMedian函数需要从数据中间取,这个功能优先级队列是没办法提供的
解决思路:
解决这个问题我们必然是会用到有序数据结构的,本题所用到的数据结构是两个优先级队列
中位数是有序数组最中间的元素
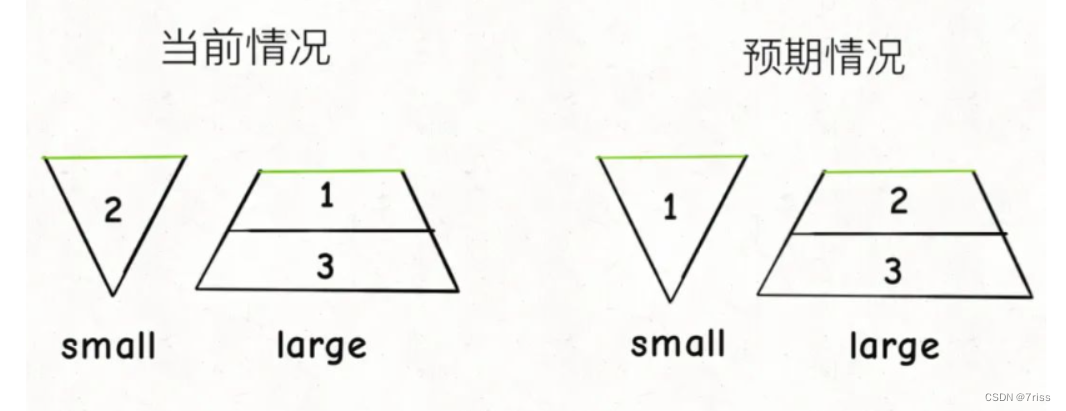
我们可以将有序数组抽象成一个倒三角形(从大到小),宽度可以视为元素的大小,那么这个倒三角形的中部就是计算中位数的元素
将这个倒三角形从中间切成两半,编程一个小倒三角形和一个梯形
这个小的倒三角形相当于一个从小到大的有序数组,这个梯形相当于一个从大到小的有序数组
他们分别可以是大顶堆和小顶堆,中位数就是他们的堆顶元素
但是梯形虽然是小顶堆,但其中的元素是较大的,我们称其为
large,倒三角虽然是大顶堆,但是其中元素较小,我们称其为small。当然,这两个堆需要算法逻辑正确维护,才能保证堆顶元素是可以算出正确的中位数,我们很容易看出来,两个堆中的元素之差不能超过 1。(这其实就是在限制实现addNum方法)
假设元素总数是
n
- 如果
n是偶数,我们希望两个堆的元素个数是一样的,这样把两个堆的堆顶元素拿出来求个平均数就是中位数;- 如果
n是奇数,那么我们希望两个堆的元素个数分别是n/2 + 1和n/2,这样元素多的那个堆的堆顶元素就是中位数。
因此,我们可以得到代码如下:
class MedianFinder {
private PriorityQueue<Integer> large;
private PriorityQueue<Integer> small;
public MedianFinder() {
// 小顶堆
large = new PriorityQueue<>();
// 大顶堆
small = new PriorityQueue<>((a, b) -> {
return b - a;
});
}
public double findMedian() {
// 如果元素不一样多,多的那个堆的堆顶元素就是中位数
if (large.size() < small.size()) {
return small.peek();
} else if (large.size() > small.size()) {
return large.peek();
}
// 如果元素一样多,两个堆堆顶元素的平均数是中位数
return (large.peek() + small.peek()) / 2.0;
}
public void addNum(int num) {
// 后文实现
}
}
那addNum方法具体要如何实现呢?
每次调用addNum方法的时候都比较以下large和small的元素个数?谁的元素少就加到谁那里,如果它们的元素一样多,默认加到large里面
// 有缺陷的代码实现
public void addNum(int num) {
if (small.size() >= large.size()) {
large.offer(num);
} else {
small.offer(num);
}
}
但是这样还是会有问题的,比如
addNum(1),现在两个堆元素数量相同,都是0,所以默认把1添加到large堆。
addNum(2),现在large的元素比small的元素多,所以把2添加到small堆中。
addNum(3),现在两个堆都有一个元素,所以默认把3添加到large中。
调用findMedian,预期的结果应该是2,但是实际的到的结果是1
由图可以得到一个事实就是我们的梯形和小倒三角形都是由原始的大倒三角从中间切开得到的,那么梯形中的最小宽度要大于等于小倒三角的最大宽度,这样它俩才能拼成一个大的倒三角!也就是说,我们在addNum的时候不仅要维护large和small的元素个数之差不超过1,还要维护large堆的堆顶元素要大于等于small堆的堆顶元素
那我们如何实现呢?
我们可以这样实现,当我们想要往large里添加元素,不能直接添加,而是要先往small里添加,然后再把small的堆顶元素加到large中,向small中添加元素同理
这样做的原理是什么呢?
假设我们准备向large中插入元素:
如果插入的num小于small的堆顶元素那么num就会留在small堆里,
为了保证两个堆的元素数量之差不大于1,作为交换,把small堆顶部的元素再插到large堆里
如果插入的num大于small的堆顶元素,那么num就会成为small的堆顶元素,最后还是会被插入large堆中
反之,向small中插入元素是一个道理,这样就巧妙地保证了large堆整体大于small堆且两个堆的元素之差不超过1,那么中位数就可以通过两个堆的堆顶元素快速计算了
// 正确的代码实现
public void addNum(int num) {
if (small.size() >= large.size()) {
small.offer(num);
large.offer(small.poll());
} else {
large.offer(num);
small.offer(large.poll());
}
}
addNum方法时间复杂度 O(logN),findMedian方法时间复杂度 O(1)。
完整代码如下:
class MedianFinder {
private PriorityQueue<Integer> small;
private PriorityQueue<Integer> large;
public MedianFinder() {
small=new PriorityQueue<>();
large=new PriorityQueue<>((a,b)->{
return b-a;
});
}
public void addNum(int num) {
//当两个堆的元素个数相同的时候,向large中添加元素,在向large添加元素之前,先将元素添加到small,再将small的堆顶元素添加到large
if(small.size()>=large.size()){
small.offer(num);
large.offer(small.poll());
}else{
large.offer(num);
small.offer(large.poll());
}
}
public double findMedian() {
//如果两个堆的元素相同就返回两个堆的堆顶元素平均值
//如果两个堆的元素个数不相同就返回元素个数比较多的堆顶元素
if(small.size()>large.size()){
return small.peek();
}else if(small.size()<large.size()){
return large.peek();
}
return (small.peek()+large.peek())/2.0;
}
}