数字信号处理2：频率

news2024/9/22 1:01:26

频率这个东西，说实话，我记得好像是初中还是小学的时候，刚接触三角函数的时候老师就已经开始给我们教频率了，但是，因为一直没有碰过信号，所以对频率也就没怎么关注过。

频率就是周期的倒数，这是最直接的定义，所以，从这个角度出发，是希望信号的时间特性（不管是连续还是离散信号）都会相应的影响到频率特性。

首先，书上给出了一个很经典的例子：

$x_a(t)=Acos(\Omega t+\theta)$

我西安画一下这个函数：

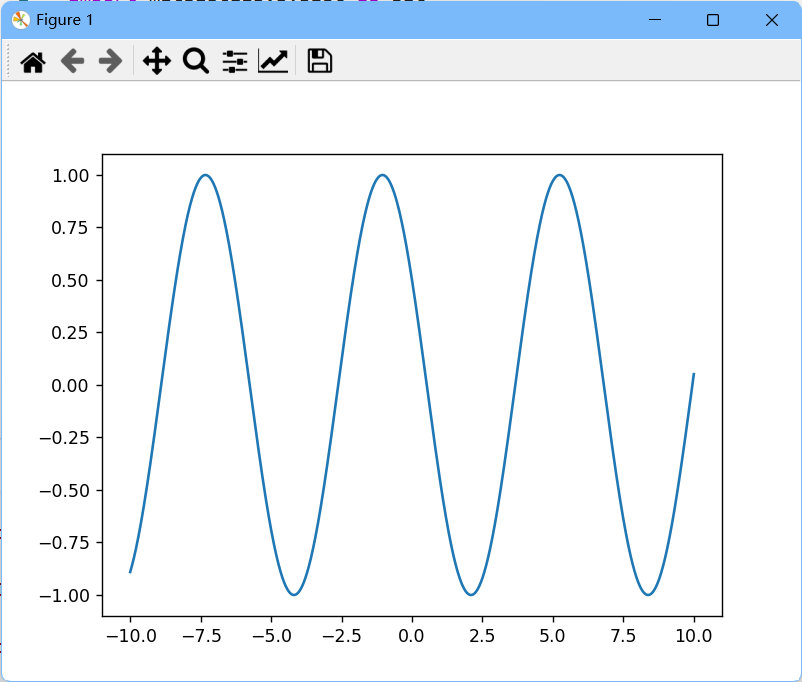
根据公式，可以知道，该信号是由三个参数表征的：振幅、频率、相位，这里我设的振幅是1，频率是1，相位是 $\pi/3$ ,通常，会用周期数/秒或者是hi赫兹Hz为单位的频率F来代替 $\Omega$ ：

$\Omega=2\pi F$

上面的这个模拟信号，我们可以用这三个属性来表征：

（1）对于固定频率值F，该信号是周期的（三角函数有周期性）

（2）不同频率的连续时间想好是可以自我区分的

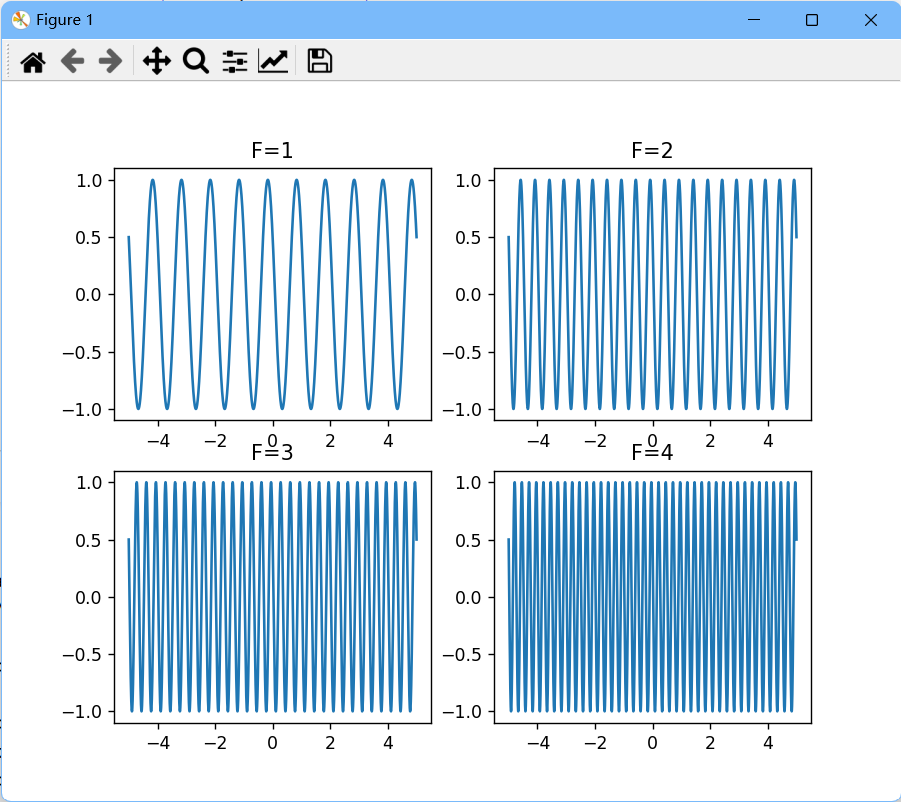
（3）增大F会导致信号振荡率的增大，也就是说，随着F增大，给定时间间隔内就会包含更多的周期（数学上你就能解释）

来看一个四个不同频率的信号：

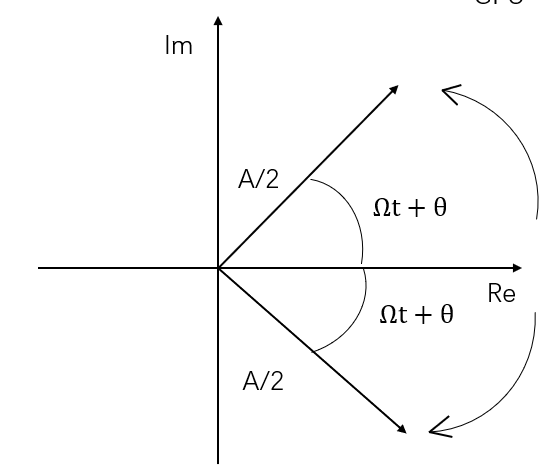
使用欧拉恒等式：

$e^{\pm j \varphi }=cos\varphi+jsin\varphi$

为了使得数学方面的方便些，引入负频率：

然后这个信号就可以写成：

$x_a(t)=\frac{A}{2}e^{j(\Omega t+\theta)}+\frac{A}{2}e^{-j(\Omega t+\theta)}$

这个型号是可以通过两个等幅的复共轭指数型号的相加得到的，这种相加操作有时候被称为移相器，正频率对应的是逆时针转动，负频率对应的是顺时针转动。

离散信号：

它实际上，从刚才给的cos函数出发，也没啥区别，顶多就是，t变成了样本，意思是说，自变量不再是连续变化，而是逐点采样：

大概就是这个样子，我就让他逐点取值，取极少的点，我想这不就离散了嘛，就是说，在上面的式子里，t的变化不再是连续的，他就是从离散的点集中取值。

$x_a(t)=Acos(\omega t+\theta)$

和连续时间信号相反的是，离散时间信号由下列属性表征：

（1）仅当其频率f是有理数的时候才是周期的；

（2）频率被 $2\pi$ 的整数倍分割的离散时间信号是相同的信号；

（3）离散时间信号的最高振荡率在 $\omega=\pm \pi$ 或者 $f=\pm \frac{1}{2}$ 时到达。

谐波相关的复指数信号：

有些情况下，要处理一组谐波相关的复指数信号，这些信号是一组周期复指数信号，其基本频率是正频率的倍数。

我搜了一下谐波的定义：谐波(harmonic wavelength)，是一个数学或物理学概念，是指周期函数或周期性的波形中能用常数、与原函数的最小正周期相同的正弦函数和余弦函数的线性组合表达的部分。从严格的意义来讲，谐波是指电流中所含有的频率为基波的整数倍的电量，一般是指对周期性的非正弦电量进行傅里叶级数分解，其余大于基波频率的电流产生的电量。

连续时间指数信号：

连续时间、谐波谐波线管指数信号的基本形式：

$s_k(t)=e^{jk\Omega t}=e^{j2\pi k F_0t},k=0,\pm1,\pm2,\cdots$

对于每一个k， $s_k(t))$ 是基本周期为 $1/(k F_0)=T/k$ 或者基本频率是 $kF_0$ 的周期信号，那么我们可以发现一个很有意思的事情：周期是 $T_p/k$ 的信号，同时也是 $k(T_p/k)=T_p$ 的周期信号，所以说，我们看到的所有的 $s_k(t))$ 信号都有着公共周期T，也就是说，如果 $k_1\neq k_2$ ，那么 $s_{k1} (t) \neq s_{k2}(t)$ ,