描述

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于

2.假设 nums[-1] = nums[n] = -∞

3.对于所有有效的 i 都有 nums[i] != nums[i + 1]

4.你可以使用O(logN)的时间复杂度实现此问题吗？

数据范围：

1 ≤ nums.length ≤ 2×105 

−2^31 <= nums[i] <= 2^31−1

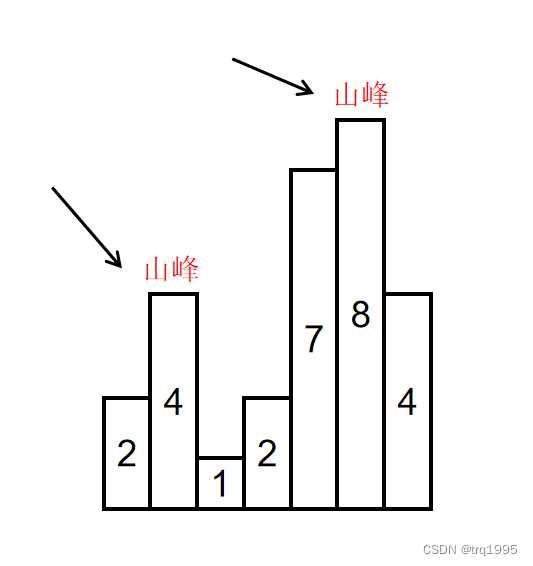
如输入[2,4,1,2,7,8,4]时，会形成两个山峰，一个是索引为1，峰值为4的山峰，另一个是索引为5，峰值为8的山峰，如下图所示：

示例1

输入：

[2,4,1,2,7,8,4]

返回值：

1

说明：

4和8都是峰值元素，返回4的索引1或者8的索引5都可以    

示例2

输入：

[1,2,3,1]

返回值：

2

说明：

3 是峰值元素，返回其索引 2 

方法一：暴力遍历

直接 for 循环遍历，找高于左右两边的峰值返回即可，时间复杂度 O(n)

方法二：二分筛选

因为条件中说明相邻值不会相等，且 nums[-1] 和 nums[n] 都为负无穷，所以我们可以判断：

1、如果值 i 向左递增，那他的左边一定有峰值

2、如果值 i 向右递增，那右边一定有峰值

3、如果值 i 的左或右递减，那就不一定有峰值

因为题目要求找到任意一个峰值即可，所以我们可以直接舍弃递减的部分，只去找递增的部分，时间复杂度 O(logn)

实现：

1、特殊条件判断

2、判断中间点 mid 是否为峰值

3、判断左或右递增

4、进入左侧或右侧，重复2，3过程

    public int findPeakElement (int[] nums) {
        // write code here
        if (nums == null || nums.length == 0) {
            return -1;
        }
        int length = nums.length;
        if (length == 1) {
            return 0;
        }
        return findTop(nums, 0, length-1);
    }

    // 递归查找峰值
    public int findTop (int[] nums, int start, int end) {
        if (start >= end - 1) {
            return isTop(nums, start) ? start : (isTop(nums, end) ? end : -1);
        }
        int mid = (start + end) / 2;
        if (isTop(nums, mid)) {
            return mid;
        }
        if (isLeftHasTop(nums, mid)) {
            return findTop(nums, start, mid);
        } else {
            return findTop(nums, mid, end);
        }
    }

    // 判断左边是否一定有峰值
    public boolean isLeftHasTop (int[] nums, int mid) {
        return nums[mid-1] > nums[mid];
    }

    // 判断给定点是否为峰值
    public boolean isTop(int[] nums, int pos) {
        if (pos == 0) {
            return nums[pos] > nums[pos+1];
        }
        if (pos == nums.length-1) {
            return nums[pos] > nums[pos-1];
        }
        return nums[pos] > nums[pos-1] && nums[pos] > nums[pos+1];
    }