目录
- 题目截图
- 题目分析
- ac code
- 树状数组模版
- 树状数组
- 总结
题目截图


题目分析
- 直接模拟的话就是平方复杂度,会超时间复杂度
- 我们删掉一个最小的,然后就要删次小的,如何找到其中间隔的距离呢?
- 间隔中可能有一些又被删掉了?怎么记录剩下的呢?
- 我们通过树状数组记录,query(i, j)表示位于[i, j]中有多少个元素已经被删除了
- 因此,我们需要逐个击破,先看看需要摆到第一个位置的元素现在的位置idx是多少,假设之前放到第一个元素原来的位置是pre
- 如果说pre < idx:那就好办直接从pre移动到idx, ans += idx - pre - query(pre, idx)
- 反之,需要先移动到n,再从1移动到idx: ans += (n - pre - query(pre, n)) + (idx - query(1, idx))
- 最后,加上n次删除ans += n
- 实际上我们需要在脑子里虚拟维护一个1,2,3,…,n的数组
ac code
# 树状数组模板
class BIT:
def __init__(self, n):
self.tree = [0] * n
# 将下标 i 上的数加一
def inc(self, i: int) -> None:
while i < len(self.tree):
self.tree[i] += 1
i += i & -i # add lowbit to right father
# 返回闭区间 [1, i] 的元素和
def sum(self, i: int) -> int:
res = 0
while i > 0:
res += self.tree[i]
# i &= i - 1
i -= i & -i # minus lowbit to left father
return res
# 返回闭区间 [left, right] 的元素和
def query(self, left: int, right: int) -> int:
return self.sum(right) - self.sum(left - 1)
class Solution:
def countOperationsToEmptyArray(self, nums: List[int]) -> int:
n = len(nums)
ans = n
t = BIT(n + 1)
pre = 1
# 把数组先转成1到n
# 然后再得到最后希望的位置
# new_nums[0]表示最后排在第0个位置的应该是new_nums[0]
new_nums = sorted(range(n), key = lambda x: nums[x])
for k, idx in enumerate(new_nums):
print(k, idx)
idx += 1
# pre现在位于第一位,现在希望idx位于第一位
if pre <= idx:
ans += idx - pre - t.query(pre, idx) # query得到的是中间删除的个数
else:
ans += (n - pre - t.query(pre, n)) + (idx - t.query(1, idx))
t.inc(idx)
pre = idx
return ans
树状数组模版
# 树状数组模板
class BIT:
def __init__(self, n):
self.tree = [0] * n
# 将下标 i 上的数加一
def inc(self, i: int) -> None:
while i < len(self.tree):
self.tree[i] += 1
i += i & -i # add lowbit to right father
# 返回闭区间 [1, i] 的元素和
def sum(self, i: int) -> int:
res = 0
while i > 0:
res += self.tree[i]
# i &= i - 1
i -= i & -i # minus lowbit to left father
return res
# 返回闭区间 [left, right] 的元素和
def query(self, left: int, right: int) -> int:
return self.sum(right) - self.sum(left - 1)
树状数组
是一个基于二进制的数据结构,可以进行高效的1.单点修改,单点查询,2.区间修改,单点查询,3.区间查询,区间修改
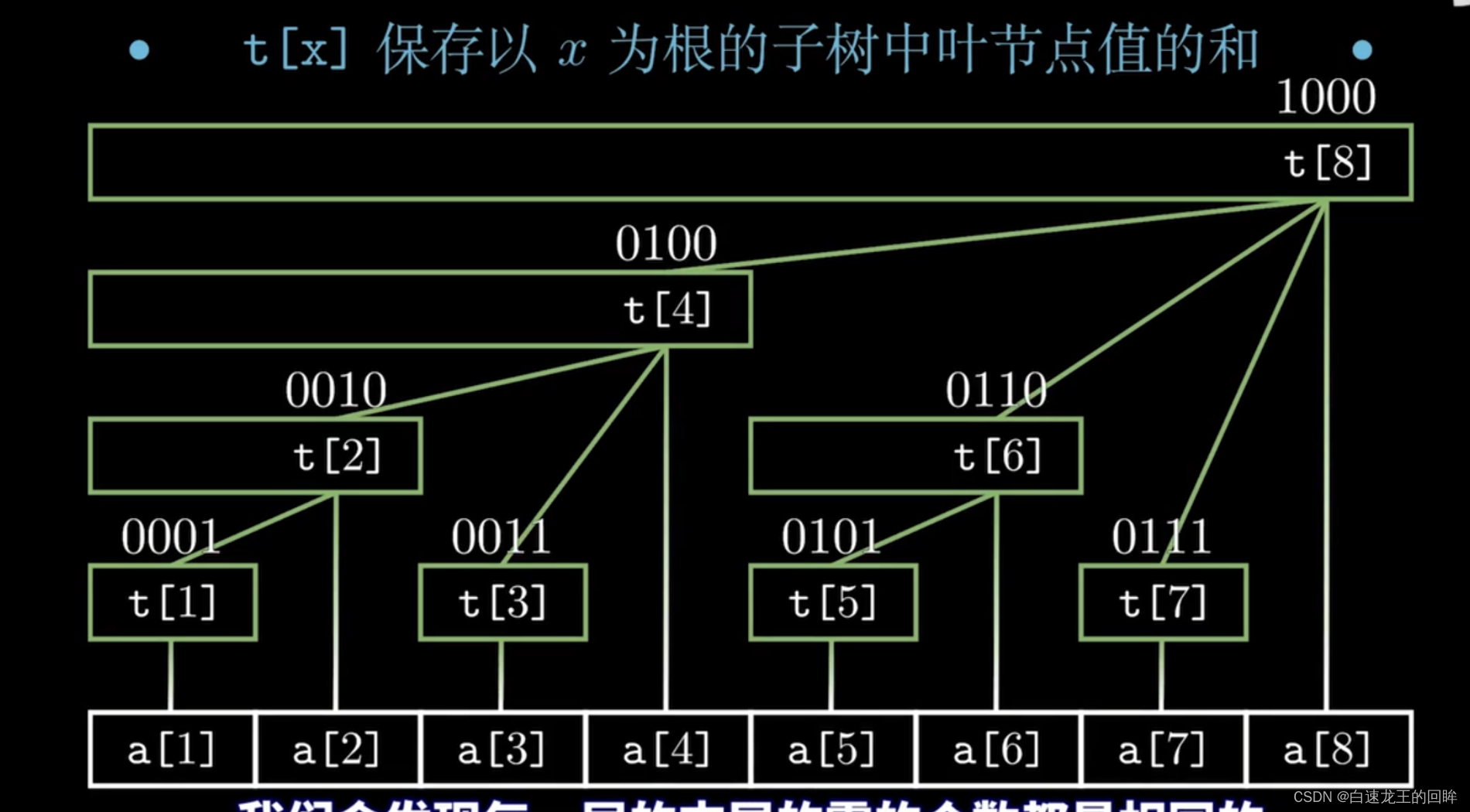
这里需要定一个lowbit的概念,也就是当前二进制最低位1跟0组成的新二进制:
fa = child + lowbit(child) 这是一个关键的性质
- 对于修改而言:直接当前节点加完后,对fa节点加即可
- 对于查询而言:要考虑新的节点child - lowbit(child),最后全部加起来即可
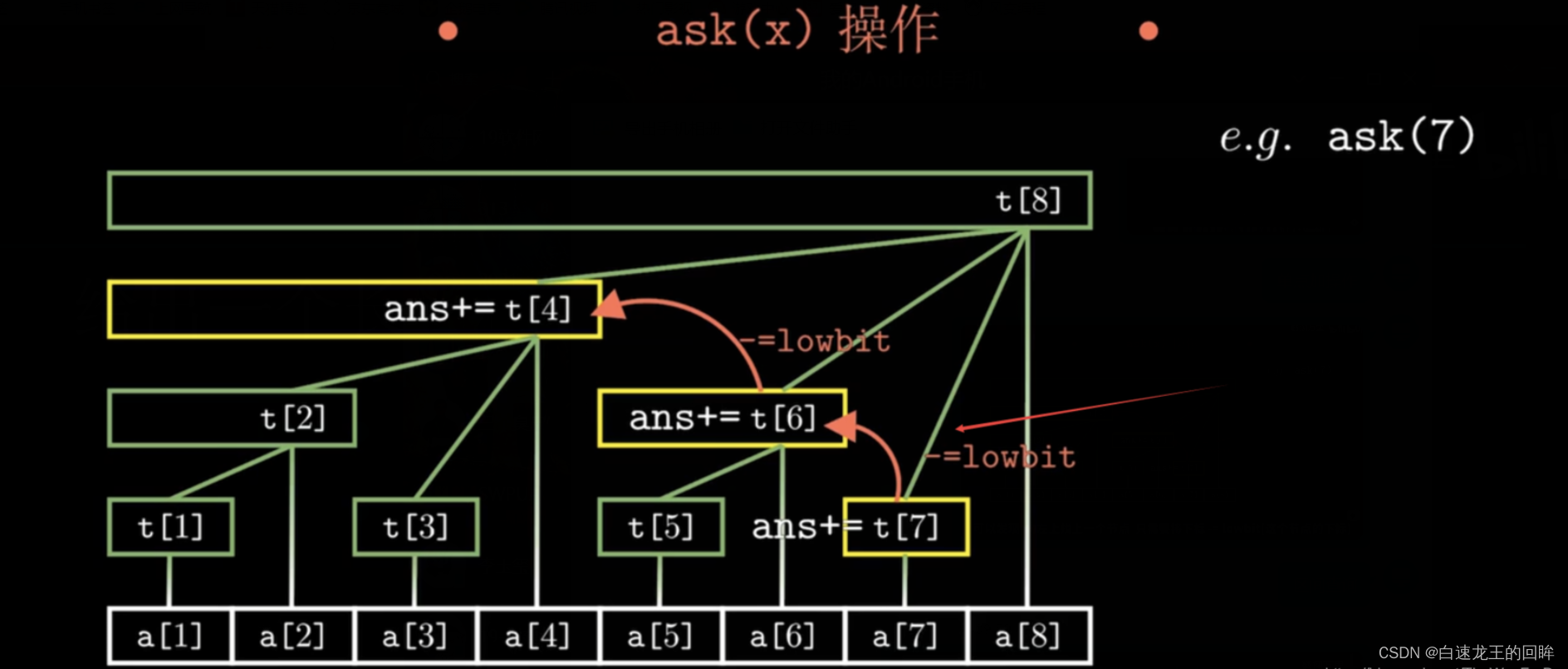
总结
- 这是一道关于下标数组的问题
- 删除后如果记录当前删除节点和之前删除节点中移动的存活的节点树
- 考虑使用树状数组快速查询