优先级队列(大根堆与小根堆)
文章目录
- 优先级队列(大根堆与小根堆)
- 堆的介绍
- 模拟堆
- 以数组模型为例,创建堆
- 向下调整(shiftDown)
- 入队(push)及向上调整(shiftUp)
- 出堆及获取堆顶元素
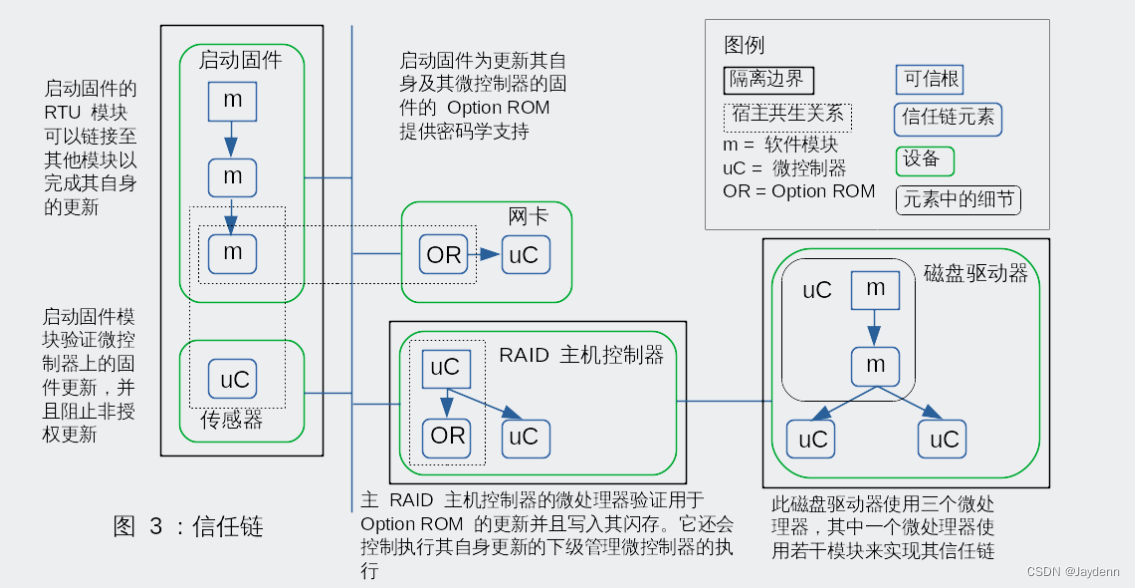
堆的介绍
优先级队列(PriorityQueue)其实就是所谓的堆,堆是一颗完全二叉树下的一种形态。存储数据在堆中为何是完全二叉树呢?是这样的,使用完全二叉树时可以避免空间的浪费,这也是堆的存储模式特别之处,如果是一些不连续的数组,采用顺序表存储更好。
堆的使用:

这是最简单的创建一个堆,我们可以看见,堆的特别之处是可以用于排序,所以对于排序的几种方法中,就有堆排序这种方案,Java中提供的默认堆是大根堆。
堆分为两种,大根堆和小根堆,根据名称可知大根堆就是最大的数字就是根节点,且满足每颗子树都是大根堆,此时该树就是大根堆,小根堆也是如此。
如图:

需要每颗子树都满足大根堆/小根堆的条件才算做堆。
模拟堆
接下来使用代码来建造一个堆,首先我们要知道堆有哪些功能,可以做那些事情,堆的基本功能如下,堆在加入元素时会自动排列好,使得堆依旧有序。
public class Test {
public void use() {
PriorityQueue<Integer> queue = new PriorityQueue<>();
queue.add(0);//添加元素到堆中
queue.offer(0);//添加元素到堆中
queue.isEmpty();//判断堆中是否还有元素
queue.size();//计算堆中还有多少元素
queue.peek();//查看堆首元素
queue.poll();//弹出堆首元素
}
}
在源码中,堆会自动扩容,所以接下来我们需要模拟实现一个堆也需要添加这项功能。
以数组模型为例,创建堆
创建一个初始化堆:
public class PriorityQueue {
//创建一个全局变量用于排序(存储)
public int[] elem;
//记录使用空间的大小
public int usedSize;
//初始大小设置为10
public PriorityQueue() {
this.elem = new int[10];
}
//扩容方法
private void superSet(){
//直接将数组扩大两倍
elem = Arrays.copyOf(elem,elem.length*2);
}
}
上面使用了扩容,那接下来就需要判断数组满否和使用空间的大小:
public class PriorityQueue {
//判断空间是否满了
public boolean isFull() {
return usedSize == elem.length;
}
//返回堆中元素个数
public int size(){
return useSize;
}
}
接下来就开始建堆:
public class PriorityQueue {
//建堆方法
public int[] createHeap(int[] array) {
for (int i = 0; i < array.length; i++) {
//判断数组满否
if(isFull()){
//扩容
superSet();
}
elem[i]=array[i];
usedSize++;
}
//从最低最右的子树开始建堆
for (int parent = (usedSize-2)/2; parent >=0 ; parent--) {
//调用向下建堆方法
shiftDown(parent,usedSize);
}
//将建好的数组返回
int[] ret = new int[usedSize];
for (int i = 0; i < usedSize; i++) {
ret[i] = elem[i];
}
return ret;
}
}
向下调整(shiftDown)

//向下建堆
public class PriorityQueue {
//将父节点和边界值传入,len是代表最后元素的下标
private void shiftDown(int parent,int len){
//得到孩子下标,因为需要和孩子下标对比
int child = 2*parent+1;
//循环条件:至少有一个左孩子
while(child<len){
//判断是否存在右孩子,只需要得到值最大的孩子即可
if(child+1<len && elem[child]<elem[child+1]){
//如果右孩子的值大于左孩子,将下标移动到右孩子
child++;
}
if(elem[parent] < elem[child]){
//如果父节点小于子节点的值,进行交换
int temp =elem[child];
elem[child]=elem[parent];
elem[parent]=temp;
//判断下一棵子树是否为大根堆
parent = child;
child = parent*2+1;
}else{
//父节点大于子节点,结束此次循环
break;
}
}
}
}
向下建堆,需要注意不能越界和对父节点与子节点的比较,如果交换好,也需要判断接下来的子树是否满足条件。
入队(push)及向上调整(shiftUp)
在入堆之前,我们不妨思考一下!入堆是从顶入好还是从底入好。

按照方法一头插相当于向下调整,在后面还需要扩大一个空间来存储加入的数字。方法二更容易的将数字向上调整,也不怕越界,遇到需要跳针的可以直接进行交换,这便是向上调整。
//向上调整
public class PriorityQueue {
//向上调整主要是针对孩子节点向上交换的过程
private void shiftUp(int child){
//得到父节点
int patent = (child-1)/2;
//判断此时是否child是否为0,为0则是最后一个节点
while(child > 0){
if(elem[parent] < elem[child]){
int tmp =elem[child];
elem[child] = elem[parent];
elem[parent] =tmp;
//继续向上
child = parent;
parent = (child-1)/2;
}else {
//子节点值小于父节点,直接结束
break;
}
}
}
}
出堆及获取堆顶元素
//弹出堆顶元素
public int pollHeap() {
//保存堆顶元素
int tmp = elem[0];
//将堆顶元素变成最后一个元素
elem[0] = elem[usedSize];
usedSize--;
//向下调整
shiftDown(0,usedSize);
//返回堆顶元素
return tmp;
}
//判断是否为空
public boolean isEmpty() {
return usedSize == 0;
}
//弹出堆顶元素
public int peekHeap() {
return elem[0];
}
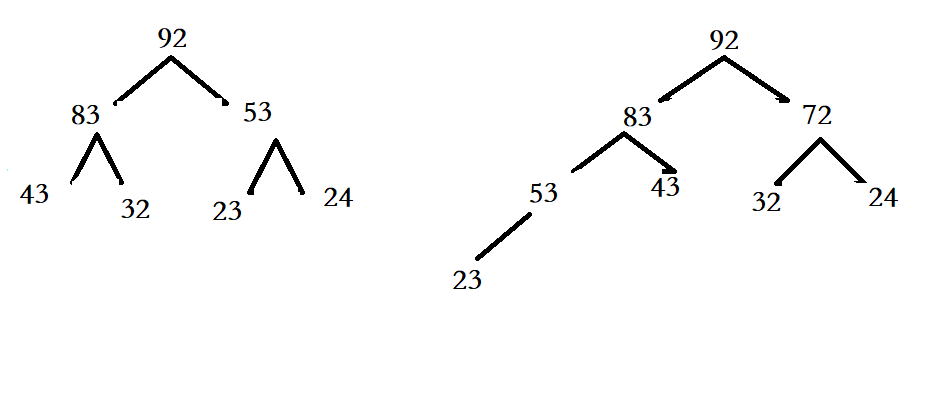
以上就是模拟堆的实现,接下来就来实验一下:
int[] array = {23,32,83,92,43,24,53};
输出:

添加:72

以上就是关于优先级队列的全部内容,关于建堆,与一些实现方法,欢迎交流🙋。